Real Computing Made Real

Preventing Errors in Scientific and Engineering Calculations

Forman S. Acton

• Publisher: Dover Publications
• Year: 2013
• Print ISBN: 9780486442211
• eBook ISBN: 9780486152936
• Topic: Mathematics
• Subtopic: Discrete Mathematics
• Index: Mathematics

Engineers and scientists who want to avoid insidious errors in their computer-assisted calculations will welcome this concise guide to trouble-shooting. Real Computing Made Real offers practical advice on detecting and removing bugs. It also outlines techniques for preserving significant figures, avoiding extraneous solutions, and finding efficient iterative processes for solving nonlinear equations.
Those who compute with real numbers (for example, floating-point numbers stored with limited precision) tend to develop techniques that increase the frequency of useful answers. But although there might be ample guidance for those addressing linear problems, little help awaits those negotiating the nonlinear world. This book, geared toward upper-level undergraduates and graduate students, helps rectify that imbalance. Its examples and exercises (with answers) help readers develop problem-formulating skills and assist them in avoiding the common pitfalls that software packages seldom detect. Some experience with standard numerical methods is assumed, but beginners will find this volume a highly practical introduction, particularly in its treatment of often-overlooked topics.

A PILLOW PROBLEM

Find the smallest positive root of

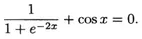
Three student proposals for solving this equation were:

1. 
2. 
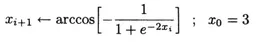
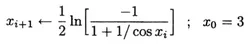
3. Newton’s method, starting with x = 3.

Who did well — and did you do any better?

Chapter 1

NONLINEAR EQUATIONS

“Thou hast damnable iterations, and art indeed able to corrupt a saint.”

Falstaff

Nonlinear equations are divided into transcendental equations (strictly, equations containing a transcendental function — but often loosely applied to almost anything nasty), algebraic equations (things with square and cube roots or other fractional powers) and polynomial equations. Of these, polynomials are sufficiently specialized to warrant separate treatment. This chapter is concerned with the rest.

Before spending time trying to solve an unfamiliar nonlinear equation carefully, plot it! Or sketch it with some care. And look at it. You may be surprised at what you see. In the event, you will probably see enough of its geometry to suggest a reasonable solution method and, conversely, to rule out other methods you might have tried. We cannot overemphasize this advice:

Look at your equation’s geometry first!

Nonlinear equations usually have several roots and they require iterative algorithms that will not work well unless started “geometrically near” a root. Without a good start, most methods will bounce all over the numerical landscape before either generating the machine equivalent of infinity or else settling down to laboriously deliver a root you probably did not want. (Newton’s method is more efficient than most, but efficiency in getting a wrong answer is not a virtue. Don’t turn Newton loose unchaperoned.)

Black-box equation solvers

Before turning to specific examples, we ought to say a few cautionary words about equation “solvers” that are now available in several mathematical software packages on PC’s and mainframe computers and, more recently, in top-of-the-line pocket calculators. Most of them are quite accurate for cleanly posed problems, that is, for problems where an uncritical application of Newton’s method will succeed. They do not invent a suitable starting value — that is a job they leave to you, with “If at first you don’t succeed ...”. They do, however, have two faults: they are frequently brute-force inefficient and they do not have the ability to reformulate an ill-conditioned problem — or even to detect its troubles. They just give you a poor answer, without comment. Caveat emptor!

A sine and a line

Let’s explore a simple example: Find the smallest positive root of the equation system

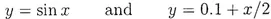
(1) (2)

which, being the sine curve and a straight line with slope 1/2 and a small intercept, 0.1, is easy to sketch (figure 1). Since the line is fairly flat, an iterative procedure comes to mind:

Step 1. Having an x, we move vertically to the line via

y ← 0.1 + x/2.

Step 2. Using this y we move horizontally to the sine curve via

x ← arcsin y

then go to Step 1.

We show one possible iteration, starting at 0.48, in our figure 1. In practice we usually will combine the steps to execut...

Table of contents

• Title Page
• Copyright Page
• Table of Contents
• ACKNOWLEDGMENTS
• AN EXHORTATION
• Chapter 0 - TOOLS OF THE TRADE
• A WORKSHOP FOR PRACTICE IN SKETCHING FUNCTIONS
• GLOOMY MUSINGS: - Correctness, Efficiency and Responsibility in Computation
• Chapter 1 - NONLINEAR EQUATIONS
• Chapter 2 - PRESERVING SIGNIFICANT DIGITS
• Chapter 3 - QUADRATURES
• Chapter 4 - RECURRENCE RELATIONS
• Chapter 5 - CHOOSING AND TUNING AN ALGORITHM
• ANSWERS TO MOST OF THE EXERCISES
• INDEX