Stability by Fixed Point Theory for Functional Differential Equations

T. A. Burton

• Publisher: Dover Publications
• Year: 2013
• Print ISBN: 9780486453309
• eBook ISBN: 9780486153322
• Topic: Mathematics
• Subtopic: Differential Equations
• Index: Mathematics

This book is the first general introduction to stability of ordinary and functional differential equations by means of fixed point techniques. It contains an extensive collection of new and classical examples worked in detail and presented in an elementary manner.
Most of this text relies on three principles: a complete metric space, the contraction mapping principle, and an elementary variation of parameters formula. The material is highly accessible to upper-level undergraduate students in the mathematical sciences, as well as working biologists, chemists, economists, engineers, mathematicians, physicists, and other scientists using differential equations. It also introduces many research problems that promise to remain of ongoing interest.

Chapter 1

Half-linear Equations

1.1 Statement of the problem

This section is an elementary introduction to the formulations of fixed point problems in differential equations. These formulations serve two purposes. First, they give a brief introduction to the kinds of problems we will be considering. But, more importantly, they offer motivation for the properties and results which we present in the next section; those properties are fundamental in the study of stability by fixed point theory.

Many different kinds of problems can be solved by means of fixed point theory. Generally, to solve a problem with fixed point theory is to find:

(a) a set S consisting of points which would be acceptable solutions;

(b) a mapping P : S → S with the property that a fixed point solves the problem;

(c) a fixed point theorem stating that this mapping on this set will have a fixed point.

We will be primarily interested in functional differential equations, but we begin with an ordinary differential equation

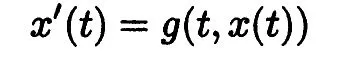
(1.1.1)

where g : [0, ∞) × Rⁿ → Rⁿ is continuous. To start us on our way we will discuss problems which are central to the study and motivate the contents of future sections. Several concepts may be used here which will be more fully defined and discussed later.

Example 1.1.1 An existence theorem. Perhaps the most basic problem concerning (1.1.1) is to find a solution through a given point (t₀, x₀) ∈ [0, ∞) × Rⁿ defined on some interval [t₀, t₀ + γ] and satisfying (1.1.1) on that interval.

For this problem, our first guess would be that the set S should consist of differentiable functions φ : [t₀, t₀ + γ] → Rⁿ with φ(t₀) = x₀. Next, the simplest way to find a mapping is to formally integrate (1.1.1) and obtain

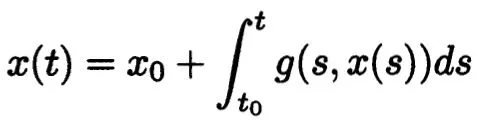
so that the mapping P on S is defined by

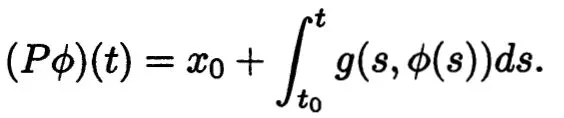
A fixed point will certainly satisfy the equation. Since our...

Table of contents

• Title Page
• Copyright Page
• Dedication
• Preface
• Table of Contents
• Chapter 0 - Introduction and Overview
• Chapter 1 - Half-linear Equations
• Chapter 2 - Classical Problems, Harmless Perturbations
• Chapter 3 - Borrowing Coefficients
• Chapter 4 - Schauder’s Theorem: A Choice
• Chapter 5 - Boundedness, Periodicity, and Stability
• Chapter 6 - Open Problems, Global Nonlinearities
• Chapter 7 - Appleby’s Stochastic Perturbations
• References
• Author Index
• Subject Index