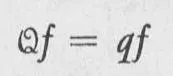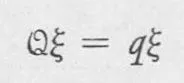1-1 EIGENVALUE PROBLEMS IN QUANTUM MECHANICS
The mathematics and physics that are relevant to quantum chemistry are, almost without exception, oriented toward the solution of a particular kind of problem, the calculation of properties of a molecular system from the fundamental properties (charge, mass) of the particles composing the system. A good example of this is the calculation of the energy of the electrons in a molecule, using only the charge of the electron, Planck’s constant, and so forth. The reader is probably already aware of the nature of the answer to this problem. There are a number of discrete values for the energy which the electrons in the molecule can assume up to a point, but higher values for the electronic energy occur in a continuous range. These energy values are shown qualitatively in Fig. 1-1. Quantum mechanics does provide the result that some physical quantities may take on only some values, not all values, as experiments indicated. The allowed values for a physical quantity are called eigenvalues, from the German for characteristic values. A particular physical quantity may assume an eigenvalue from a continuum, or perhaps from a finite or infinite discrete set of eigenvalues. The energy of an atom, for instance, may take on one of an infinite number of discrete values, as well as values from a higher-lying range of continuous eigenvalues, called the continuum. More often than not, chemistry is concerned with the discrete eigenvalues of a quantity, rather than its continuum of eigenvalues.
Figure 1-1 Eigenvalues of the energy of a molecule.
The mathematical problem of finding the eigenvalues of a quantity is called an eigenvalue problem; it is usually cast in the form of an equation called an eigenvalue equation. An eigenvalue equation for a physical quantity Q has the deceptively simple appearance
In this equation, f is a function, called the eigenfunction for the quantity Q, with the eigenvalue q. The element Q is called an operator, and the statement Qf tells us to change the function f into a new function, according to a set of instructions implicit in the definition of the operator Q. The eigenvalue equation, Eq. 1-1, then informs us that, by applying these “instructions” of the operator Q to ƒ, we get merely a multiple, q, of the function f. The function Qf differs from the function f by a multiplicative constant q. It may very well be the case that several eigenfunctions have the same eigenvalue; that is, Qƒ1 = qƒ1 Qƒ2 = qƒ2, and so forth. If this is the case, the eigenvalue q is said to be degenerate; and the number of eigenfunctions that have the same eigenvalue is called the degree of degeneracy.
Operators may simply be numbers or functions; for example, the operator X may be defined by the instruction “multiply the operand function by x”; thus, X x2 = x3. On the other hand, operators may be more complex than just numbers or functions. For example, the student has already used the operator (although probably not by that name) Δ which means, or is defined by the instructions, “evaluate the change in.” For example, if we operate Δ on the thermodynamic function H, the enthalpy, we get a new function ΔH, the change in the enthalpy, ΔH = H2 − H1. Another operator that is familiar is d/dx, meaning, “evaluate the derivative with respect to x. ”
It is the job of quantum mechanics to tell us how to form operators corresponding to the physical quantities which we wish to measure. Our task for the moment will be to learn how to solve the eigenvalue equations for such operators, and especially the vocabulary and concepts that are used to discuss the solutions. Quantum mechanics itself, however, grew up from two different points of view, which represent two analogous mathematical formulations of eigenvalue problems.
The first of these points of view is the wave mechanics of Schrödinger In wave mechanics, operators are differential expressions, such as the operator d/dx referred to above, and the eigenvalue equation then takes the form of a differential equation, and relies on the calculus for its solution. The second formulation is the matrix mechanics of Heisenberg, in which operators are represented by algebraic entities called matrices; instead of a function in the eigenvalue equation, the matrix operator operates on a vector ξ to transform ξ into a vector parallel to ξ, but q times as long:
Equation 1–2 is the matrix-mechanical formulation of the eigenvalue problem. Matrices and vectors are defined and discussed in detail in Chapter 3. As in Eq. 1–1, q is the eigenvalue of the quantity Q, ξ is the eigenvector, and Q is the operator represented as a matrix. The solution of this form of the eigenvalue problem relies on algebra.
These apparently different mathematical and physical approaches to quantum mechanical problems are really deeply interrelated; the work of Dirac shows the underlying equivalence of the two points of view, as well as of the corresponding mathematical techniques.
1–3 SCOPE OF THIS BOOK
With our course thus determined by the kinds of problems we wish to be able to set up, solve, and understand, we shall proceed first to a study of a certain class of functions germane to eigenfunction problems, then to a number of aspects of vector algebra and matrix algebra, finally to a synthesis of the two points of view of eigenvalue problems. We shall conclude with a study of classical mechanics to see how the vibrations of a mechanical system, such as a molecule, may be formulated as an eigenvalue problem. We shall also attempt to formulate Newtonian mechanics in such a way that the connection to quantum mechanics is clear.
Along the way, we shall learn some methods of solving eigenvalue problems, and take up applications of interest in chemistry. Our emphasis throughout will be primarily on concepts, secondarily on methods, and only lastly on the detailed proofs of the mathematical theorems. At the end of each chapter, a set of problems is given. Answers and hints for solution for many of the problems are found at the back of the book.
Problem
1. Find the eigenfunctions of the operator d/dx.