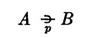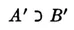Philosophic Foundations of Quantum Mechanics

Hans Reichenbach

• Publisher: Dover Publications
• Year: 2012
• Print ISBN: 9780486404592
• eBook ISBN: 9780486150109
• Topic: Physical Sciences
• Subtopic: Physics
• Index: Physics

Physics concerns direct analysis of the physical world, while philosophy analyzes knowledge about the physical world. This volume combines both disciplines for a philosophical interpretation of quantum physics — an interpretation free from the imprecision of metaphysics, offering a view of the atomic world and its quantum mechanical results as concrete as the visible everyday world.
Written by an internationally renowned philosopher who specialized in symbolic logic and the theory of relativity, this approach consists of three parts. The first section, which requires no background in math or physics, reviews the basics of quantum mechanics, outlining their philosophical interpretation and summarizing their results. The second part, which presupposes a knowledge of calculus, outlines the mathematical methods of quantum mechanics; and the third part blends the philosophical ideas of the first part and the mathematical formulations of the second part to develop a variety of interpretations of quantum mechanics. The author presents in-depth discussions of each interpretation, constructing a conclusion in terms of three-valued logic that offers readers a satisfactory logical form of quantum mechanics.
Focusing on clarification of concepts rather than developing problem-solving skills, this volume will prove enlightening to students of mathematics, physics, and the other sciences.

Part I

GENERAL CONSIDERATIONS

§ 1. Causal Laws and Probability Laws

The philosophical problems of quantum mechanics are centered around two main issues. The first concerns the transition from causal laws to probability laws; the second concerns the interpretation of unobserved objects. We begin with the discussion of the first issue, and shall enter into the analysis of the second in later sections.

The question of replacing causal laws by statistical laws made its appearance in the history of physics long before the times of the theory of quanta. Since the time of Boltzmann’s great discovery which revealed the second principle of thermodynamics to be a statistical instead of a causal law, the opinion has been repeatedly uttered that a similar fate may meet all other physical laws. The idea of determinism, i.e., of strict causal laws governing the elementary phenomena of nature, was recognized as an extrapolation inferred from the causal regularities of the macrocosm. The validity of this extrapolation was questioned as soon as it turned out that macrocosmic regularity is equally compatible with irregularity in the microcosmic domain, since the law of great numbers will transform the probability character of the elementary phenomena into the practical certainty of statistical laws. Observations in the macrocosmic domain will never furnish any evidence for causality of atomic occurrences so long as only effects of great numbers of atomic particles are considered. This was the result of unprejudiced philosophical analysis of the physics of Boltzmann .¹

With this result a decision of the question was postponed until it was possible to observe macrocosmic effects of individual atomic phenomena. Even with the use of observations of this kind, however, the question is not easily answered, but requires the development of a more profound logical analysis.

Whenever we speak of strictly causal laws we assume them to hold between idealized physical states; and we know that actual physical states never cor-respond exactly to the conditions assumed for the laws. This discrepancy has often been disregarded as irrelevant, as being due to the imperfection of the experimenter and therefore negligible in a statement about causality as a property of nature. With such an attitude, however, the way to a solution of the problem of causality is barred. Statements about the physical world have meaning only so far as they are connected with verifiable results; and a statement about strict causality must be translatable into statements about observable relations if it is to have a utilizable meaning. Following this principle we can interpret the statement of causality in the following way.

If we characterize physical states in observational terms, i.e., in terms of observations as they are actually made, we know that we can construct probability relations between these states. For instance, if we know the inclination of the barrel of a gun, the powder charge, and the weight of the shell, we can predict the point of impact with a certain probability. Let A be the so-defined initial conditions and B a description of the point of impact; then we have a probability implication

(1)

which states that if A is given, B will happen with a determinate probability p. From this empirically verifiable relation we pass to an ideal relation by considering ideal states A′ and B′ and stating a logical implication

(2)

between them, which represents a law of mechanics. Since we know, however, that from the observational state A we can infer only with some probability the existence of the ideal state A′, and that similarly we have only a probability relation between B and B′, the logical implication (2) cannot be utilized. It derives its physical meaning only from the fact that in all cases of applications to observable phenomena it can be replaced by the probability implication (1). What then is the meaning of a statement saying that if we knew exactly the initial conditions we could predict with certainty the future states resulting from them? Such a statement can be meaningfully said only in the sense of a transition to a limit. Instead of characterizing the initial conditions of shooting only by the mentioned three parameters, the inclination of the barrel, the powder charge, and the weight of the shell, we can consider further parameters, such as the resistance of the air, the rotation of the earth, etc. As a consequence, the predicted value will change; but we know that with such a more precise characterization also the probability of the prediction increases. From experiences of this kind we have inferred that the probability p can be made to approach the value 1 as closely as we want by the introduction of further parameters into the analysis of physical states. It is in this form that we must state the principle of causality if it is to have physical meaning. The statement that nature is governed by strict causal laws means that we can predict the future with a determinate probability and that we can push this probability as close to certainty as we want by using a sufficiently elaborate analysis of the phenomena under consideration.

With this formulation the principle of causality is stripped of its disguise as a principle a priori, in which it has been presented within many a philosophical system. If causality is stated as a limit of probability implications, it is clear that this principle can be maintained only in the sense of an empirical hypothesis. There is, logically, no need for saying that the probability of predictions can be made to approach certainty by the introduction of more and more parameters. In this form the possibility of a limit of predictability was recognized even before quantum mechanics led to the assertion of such a limit.²

The objection has been raised that we can know only a finite number of parameters, and that therefore we must leave open the possibility of discovering, at a later time, new parameters which lead to better predictions. Although, of course, we have no means of excluding with certainty such a possibility, we must answer that there may be strong inductive evidence against such an assumption, and that such evidence will be regarded as given if continued attempts at finding new parameters have failed. Physical laws, like the law of conservation of energy, have been based on evidence derived from repeated failures of attempts to prove the contrary. If the existence of causal laws is denied, this assertion will always be grounded only in inductive evidence. The critics of the belief in causality will not commit the mistake of their adversaries, and will not try to adduce a supposed evidence a priori for their contentions.

The quantum mechanical criticism of causality must therefore be considered as the logical continuation of a line of development which began with the introduction of statistical laws into physics within the kinetic theory of gases, and was continued in the empiricist analysis of the concept of causality. The specific form, however, in which this criticism finally was presented through Heisenberg’s principle of indeterminacy was different from the form of the criticism so far explained.

In the preceding analysis we have assumed that it is possible to measure the independent parameters of physical occurrences as exactly as we wish; or more precisely, to measure the simultaneous values of these parameters as exactly as we wish. The breakdown of causality then consists in the fact that these values do not strictly determine the values of dependent entities, including the values of the same parameters at later times. Our analysis therefore contains an assumption of the measurement of simultaneous values of independent parameters. It is this assumption which Heisenberg has shown to be wrong.

The laws of classical physics are throughout temporally directed laws, i.e., laws stating dependences of entities at different times and which thus establish causal lines extending in the direction of time. If simultaneous values of differ-ent entities are regarded as dependent on one another, this dependence is always construed as derivable from temporally directed laws. Thus the correspondence of various indicators of a physical state is reduced to the influence of the same physical cause acting on the instruments. If, for instance, barometers in different rooms of a house always show the same indication, we explain this correspondence as due to the effect of the same mass of air on the instruments, i.e., as due to the effect of a common cause. It is possible, however, to assume the existence of cross-section laws, i.e., laws which directly connect simultaneous values of physical entities without being reducible to the effects of common causes. It is such a cross-section law which Heisenberg has stated in his relation of indeterminacy.

This cross-section law has the form of a limitation of measurability. It states that the simultaneous values of the independent parameters cannot be measured as exactly as we wish. We can measure only one half of all the parameters to a desired degree of exactness; the other half then must remain inexactly known. There exists a coupling of simultaneously measurable values such that greater exactness in the determination of one half of the totality involves less exactness in the determination of the other half, and vice versa. This law does not make half of the parameters functions of the others; if one half is known, the other half remains entirely unknown unless it is measured. We know, however, that this measurement is restricted to a certain exactness.

This cross-section law leads to a specific version of the criticism of causality. If the values of the independent parameters are inexactly known, we cannot expect to be able to make strict predictions of future observations. We then can establish only statistical laws for these observations. The idea that there are causal laws “behind” these statistical laws, which determine exactly the results of future observations, is then destined to remain an unverifiable statement; its verification is excluded by a physical law, the cross-section law mentioned. According to the verifiability theory of meaning, which has been generally accepted for the interpretation of physics, the statement that there are causal laws therefore must be considered as physically meaningless. It is an empty assertion which cannot be converted into relations between observational data.

There is only one way left in which a physically meaningful statement about causality can be made. If statements of causal relations between the exact values of certain entities cannot be verified, we can try to introduce them at least in the form of conventions or definitions; that is, we may try to establish arbitrarily causal relations between the strict values. This means that we can attempt to assign definite values to the unmeasured, or not exactly measured, entities in such a way that the observed results appear as the causal consequences of the values introduced by our assumption. If this were possible, the causal relations introduced could not be used for an improvement of predictions; they could be used only after observations had been made in the sense of a causal construction post hoc. Even if we wish to follow such a procedure, however, we must answer the question of whether such a causal supplementation of observable data by interpolation of unobserved values can be consistently done. Although the interpolation is based on conventions, the answer to the latter question is not a matter of convention, but depends on the structure of the physical world. Heisenberg’s principle of indeterminacy, therefore, leads to a revision of the statement of causality; if this statement is to be physically meaningful, it must be made as an assertion about a possible causal supplementation of the observational world.

With these considerations the plan of the following inquiry is made clear. We shall first explain Heisenberg’s principle, showing its nature as a cross-section law, and discuss the reasons why it must be regarded as being well founded on empirical evidence. We then shall turn to the question of the interpolation of unobserved values by definitions. We shall show that the question stated above is to be answered negatively; that the relations of quantum mechanics are so constructed that they do not admit of a causal supplementation by interpolation. With these results the principle of causality is shown to be in no sense compatible with quantum physics; causal determi...

Table of contents

• Title Page
• Copyright Page
• PREFACE
• Table of Contents
• Part I - GENERAL CONSIDERATIONS
• Part II - OUTLINES OF THE MATHEMATICS OF QUANTUM MECHANICS
• Part III - INTERPRETATIONS
• INDEX