Semi-Simple Lie Algebras and Their Representations

Robert N. Cahn

• Publisher: Dover Publications
• Year: 2014
• Print ISBN: 9780486449999
• eBook ISBN: 9780486150314
• Topic: Mathematics
• Subtopic: Algebra
• Index: Mathematics

Designed to acquaint students of particle physics already familiar with SU(2) and SU(3) with techniques applicable to all simple Lie algebras, this text is especially suited to the study of grand unification theories. Author Robert N. Cahn, who is affiliated with the Lawrence Berkeley National Laboratory in Berkeley, California, has provided a new preface for this edition. Subjects include the killing form, the structure of simple Lie algebras and their representations, simple roots and the Cartan matrix, the classical Lie algebras, and the exceptional Lie algebras. Additional topics include Casimir operators and Freudenthal's formula, the Weyl group, Weyl's dimension formula, reducing product representations, subalgebras, and branching rules. 1984 edition.

XV. Subalgebras

Some examples may be illuminating as an introduction to the topic of sub-algebras. Suppose we start with the algebra G = A₅, i.e. SU (6), the traceless 6 × 6 matrices. Now one subalgebra is obtained by considering only those matrices with non-zero 4 × 4 and 2 × 2 diagonal pieces, and zeros in the 4 × 2 off- diagonal pieces. If the two diagonal blocks are required to be traceless separately, then the restricted set is the subalgebra G′ — A₃ + A₁ ⊂ A₅ = G. It is clear that we can take as the Cart an subalgebra H′ ⊂ G′ the diagonal matrices, so H′ ⊂ H. The dimension of H′ is one fewer than that of H since there is a one dimensional subspace of H proportional to the diagonal element which is +1 for the first four components and -2 on the last two.

The root vectors of G′ are just the root vectors of G which have non-zero components only in the two diagonal blocks. If the space proportional to e_α is denoted G_α, we have

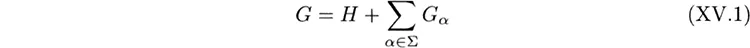
while for some set Σ′ ⊂ Σ

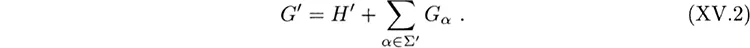
A subalgebra with this property is called regular. In addition to this SU(6) example, the subalgebras we employed in the method of parts - which were obtained by deleting dots from Dynkin diagrams - were regular. Not all subalgebras, however, are regular.

Let us consider again A₅ and a particular embedding of G′ = A₂+A₁ (SU(3) × SU(2)). We know that every matrix in the Lie algebra of SU(2) is a linear combination of σ₁, σ₂, and σ₃ and every matrix in the Lie algebra of SU(3) is a linear combination of λ₁, λ₂, ... λ₈. Let us add to these σ₀ and λ₀ which are the 3 × 3 and 2 × 2 identity matrices. Now every 6 × 6 matrix can be written in terms of

i.e. σ₀ ⊗λ_i, σ₃ ⊗λ_i, σ₁ ⊗λ_i, σ₂ ⊗λ_i, i = 0, 1, . . . 8. Now this is equivalent to regarding the six dimensional vectors in the carrier space as having two indices, with the σ acting on the first and the λ on the second.

Now suppose we consider only elements of the forms σ₀ ⊗λ_i and σ_i ⊗λ₀, Then an element of one form commutes with an element of the other. Thus these elements form a subalgebra which is A₂ + A₁. The Cartan subalgebra of the A₂ + A₁ has a basis σ₃ ⊗λ₀, σ₀ ⊗λ₃, σ₀ ⊗λ₈. The root vectors are σ₊ ⊗λ₀, σ_– ⊗λ₀, σ₀ ⊗t₊, σ₀ ⊗t-, σ₀ ⊗u, σ₀ ⊗v_–. We see that H′ ⊂ H. However, the root vectors of G′ are not among those of G. Thus, for example,

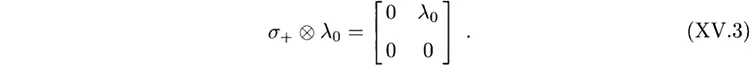
We cannot write G′ in the form Eq. (XV.2), so the subalgebra is not regular.

The six dimensional representation of A₅ gave a reducible representation of the regular subalgebra, A₃ + A₁: 6 → (4,1) + (1,2). The non-regular subalgebra, A₂ + A₁, gave an irreducible representation: 6 → (3,2). As we shall see, this is typical.

As a further example of regular and non-regular subalgebras, consider SU(2) as a subalgebra of SU(3). If the SU(2) is generated by t₊, t_–, and t_z, the SU(2) is a regular subalgebra. On the other hand, there is a three dimensional representation of SU(2). The 3 × 3 matrices of this representation are elements of SU(3) so this provides a second embedding of SU(2) in SU(3), which is not regular. Under the regular embedding, the 3 dimensional representation of SU(3) becomes a reducible 2 + 1 dimensional representation of SU(2), while under the second embedding, it becomes an irreducible representation of SU(2).

It is clear that a moderate sized algebra may have an enormous number of subalgebras. To organize the task of finding them we in...

Table of contents

• Table of Contents
• I. SU(2)
• II. SU(3)
• III. The Killing Form
• IV. The Structure of Simple Lie Algebras
• V. A Little about Representations
• VI. More on the Structure of Simple Lie Algebras
• VII. Simple Roots and the Cartan Matrix
• VIII. The Classical Lie Algebras
• IX. The Exceptional Lie Algebras
• X. More on Representations
• XI. Casimir Operators and Freudenthal’s Formula
• XII. The Weyl Group
• XIII. Weyl’s Dimension Formula
• XIV. Reducing Product Representations
• XV. Subalgebras
• XVI. Branching Rules
• Bibliography
• Index