Stability Theory of Differential Equations

Richard Bellman

• Publisher: Dover Publications
• Year: 2013
• ISBN:
  9780486150130
• Topic: Mathematics
• Subtopic: Geometry
• Index: Mathematics

Suitable for advanced undergraduates and graduate students, this was the first English-language text to offer detailed coverage of boundedness, stability, and asymptotic behavior of linear and nonlinear differential equations. It remains a classic guide, featuring material from original research papers, including the author's own studies.
The linear equation with constant and almost-constant coefficients receives in-depth attention that includes aspects of matrix theory. No previous acquaintance with the theory is necessary, since author Richard Bellman derives the results in matrix theory from the beginning. In regard to the stability of nonlinear systems, results of the linear theory are used to drive the results of Poincaré and Liapounoff. Professor Bellman then surveys important results concerning the boundedness, stability, and asymptotic behavior of second-order linear differential equations. The final chapters explore significant nonlinear differential equations whose solutions may be completely described in terms of asymptotic behavior. Only real solutions of real equations are considered, and the treatment emphasizes the behavior of these solutions as the independent variable increases without limit.

CHAPTER 1

PROPERTIES OF LINEAR SYSTEMS

1. Introduction. In this introductory chapter we shall consider the fundamental properties of solutions of the system of linear differential equations,

(1)

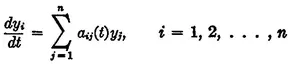
The independent variable t is to range over the interval [0, ∞], and we shall assume that the coefficient functions a_ij(t) are piecewise-continuous over any finite subinterval. Under this assumption, we may consider all integrals that appear to be Riemann integrals. For our purposes there is very little to be gained from the sophistication of the Lebesgue integral, and we prefer, in consequence, to keep our discussion on as elementary a level as possible.

We furthermore postulate that the coefficients are real functions. Occasionally, particularly in the discussion of linear systems with constant coefficients and with coefficients close to constant, we shall introduce complex solutions. For example, we may use (e^it,e^-it) as a basic set of solutions of d²u/dt² + u = 0, rather than (cos t, sin t). This is purely a matter of convenience, however, and we shall always be primarily interested in real solutions of real systems.

The only way to study the behavior of solutions of systems of linear algebraic equations or linear differential equations in any systematic fashion is to make use of the concepts of vectors and matrices. In this chapter we shall introduce these concepts and demonstrate the few results required for the theory of differential equations. No prior knowledge of vector or matrix theory will be assumed.

Exercise

Show that the nth-order linear equation

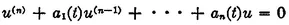
may be converted into a linear system of the type of (1) above by means of the substitutions u = u_1,, u′ = u₂, . . . , u⁽ⁿ⁻¹⁾ = u_n....

Table of contents

• Title Page
• Dedication
• Copyright Page
• PREFACE
• Table of Contents
• CHAPTER 1 - PROPERTIES OF LINEAR SYSTEMS
• CHAPTER 2 - STABILITY, BOUNDEDNESS, AND ASYMPTOTIC BEHAVIOR OF SOLUTIONS OF LINEAR SYSTEMS
• CHAPTER 3 - THE EXISTENCE AND UNIQUENESS OF SOLUTIONS OF NONLINEAR SYSTEMS
• CHAPTER 4 - THE STABILITY OF SOLUTIONS OF NONLINEAR DIFFERENTIAL EQUATIONS
• CHAPTER 5 - THE ASYMPTOTIC BEHAVIOR OF THE SOLUTIONS OF SOME NONLINEAR EQUATIONS OF THE FIRST ORDER
• CHAPTER 6 - THE SECOND-ORDER LINEAR DIFFERENTIAL EQUATION
• CHAPTER 7 - THE EMDEN-FOWLER EQUATION
• INDEX