Treatise on Harmony

Jean-Philippe Rameau

• Publisher: Dover Publications
• Year: 2012
• Print ISBN: 9780486224619
• eBook ISBN: 9780486171371
• Topic: Media & Performing Arts
• Subtopic: Classical Music

The Traité de l'harmonie of Jen-Philippe Rameau is one of the most important books in the history of Western music. Written while Rameau was still a relatively obscure organist and music master at Clermont-Ferrand, the book received but one printing during Rameau's life, in 1722, shortly before he settled in Paris. The Traité was immediately recognized as a profound advance in musical theory, however, and it established Rameau's reputation as a theorist. His book was the first to codify those principles of tonality that were to dominate the music of the West for almost two centuries. Even today the theories of Rameau remain the basis for the study of harmony.
Rameau's Traité de l'harmonie is divided into four books, the first of which presents the mathematical basis from which Rameau sought to derive his theories. Book Two may be considered the most important section of the Traité; in it Rameau generates his entire harmonic system from fundamental principles, explaining intervals, chords, and modes — everything, in fact, essential to musical composition in tonal style. Working from the principles developed in Books One and Two, Book Three treats the practical rules of composition, including such topics as harmonic modulation and chord progressions. Book Four concerns the practical art of accompaniment on harpsichord or organ, including the realization of a figured bass. Corrections added by Rameau in a supplement are included in the text, and all the musical examples have been reset in modern musical notation. In addition, two pages from a unique copy of the first issue of the first edition are given in facsimile. The translator's introduction discusses the history of the work, Rameau's mathematics, and his place in the history of music theory.

BOOK THREE

Principles of Composition

CHAPTER ONE

Introduction to practical Music

On the Scale

Just as there are only seven diatonic¹⁸⁰ sounds, i.e., seven successive degrees in the natural voice, there are likewise in music only seven notes: Do, Re, Mi, Fa, Sol, La, Si, known as the scale. The number of notes may be increased only by recommencing with the first after the last, always following the order here prescribed. These same notes thus repeated, which are only replicates of the others, are called octaves.

It is well to add the octave of the first note to the end of the scale, so as to accustom ourselves to recognize this octave, thus: Do, Re, Mi, Fa, Sol, La, Si, Do. Remember that this progression of notes, here presented in ascending order, should also be known in descending order, thus: Do, Si, La, Sol, Fa, Mi, Re, Do.

If we wish to begin and end this scale by a note different from Do (it being well to practice this, although it is contrary to the diatonic order), we need only add octaves to the other notes, just as the octave was added above. Thus, if we begin with Sol, we need only say Sol, La, Si, Do, Re, Mi, Fa, Sol, in ascending order, and Sol, Fa, Mi, Re, Do, Si, La, Sol, in descending order, and so on.

On Intervals

We must not only know how to recite the scale ascending as well as descending, and how to make it begin now on one note, now on another, but we must also observe the distance from one note to another, according to the order of the numbers; remember that this observation is to be made only in ascending.

It is from this distance that all the intervals of music are formed; these intervals, whose names are taken from the numbers of arithmetic, are called:

We have placed the numbers from which each interval derives its name above the name, for hereafter we shall use these numbers alone to designate the interval we are discussing. It is therefore important to remember that 2 designates the second, 3 the third, 4 the fourth, and so on, up to the octave, which is designated by the number 8.

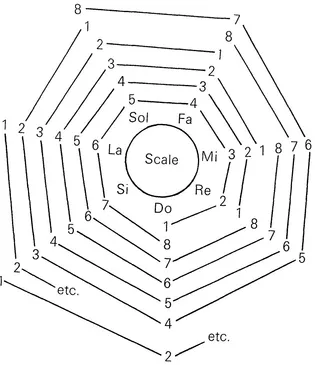
In order to find these intervals, we must first designate a note as the source or first degree; then, counting from this note to another, the same number as the number of notes counted designates the interval found between the first note and the other. For example, if we take Do as the first degree, we immediately see that Re forms a second with it, Mi a third, Fa a fourth, Sol a fifth, etc. Likewise, if we take Re as the first degree, Mi forms a second with it, Si a sixth, Do a seventh; the same is true for all other notes you wish, each of which must be designated as the first degree in turn. We ought to know these intervals so well that we can immediately say that Mi forms the fifth of La, Si that of Mi, Re that of Sol, etc. To this end, we may use the following scale. [Ex. III.1.]

Example III.1

Taking Do as the first note or first degree, we shall find a line in this scale which leads from one to two below Re, to three below Mi, and so on, continuing around up to eight which represents the octave of this same Do; for the octave, which is only a replicate (as we have already said), is always represented by the same note with the same name. Similarly, if we take Re as the first note, the figure i below it leads to 2 below Mi, to 3 below Fa, etc. These numbers mark the intervals that the notes below which they are found form with those notes beginning with 1 ; from 1 we pass to 2, to 3, to 4, etc., by means of the small lines which together form a circle from 1 to 8.

Remember that whenever we speak simply of the third, the fourth, etc., these intervals are to be taken in the scale, ascending from the note designated as the first degree, since this note is always considered to be the lowest.

We should also practice looking for descending intervals in the scale; we shall thus find that the fourth below Do is Sol, just as the fourth above Sol is Do. This is not difficult to understand, and it may be extremely useful on certain occasions.

On the inversion of Intervals

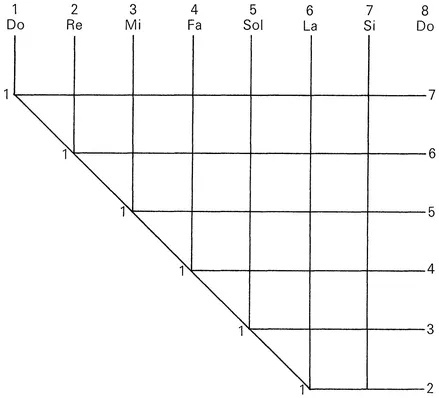
The two notes which form the octave and are basically only a single note act as limits for all intervals, since in fact all notes of the scale are contained within the octave. If we then treat the two Do’s which begin and end the scale as a single note, we shall realize immediately that, whatever other note is compared to each of these two Do’s, two different intervals cannot arise. Since the first Do is below the note being compared to it while the second is above, however, a difference will be perceived here which must be explained. [Ex. III.2.]

Considering the scale in this way, we see that Re forms a second with the first Do, and that the second Do forms a seventh with this Re; that Mi forms a third with the first Do, and that the second Do forms a sixth with this Mi; that Fa forms a fourth with the first Do, and that the second Do forms a fifth with this Fa; finally, that Sol forms a fifth with the first Do and a fourth with the second Do. We could continue in the same manner. By this means we perceive that one interval is always born of another; for if we take another note as the first degree, placing it at the beginning and end of the scale, we need only make the observations there that we have just made with regard to Do in order to find the same results, i.e., that the second of the first note will always become the seventh of the octave of this first note, etc.

Example III.2

For a fuller understanding, we must always imagine that the octave is inseparable from the note taken as the first degree, so that after having compared a note to this first degree, we then compare it to the octave of this first degree. Two intervals will thus arise, the first of which is called fundamental or principal and the second inverted; for if we compare Do to Mi and then Mi to Do, we find there only an inversion of the comparison. Similarly with numbers, assuming that 8 and 1 represent the same note, the comparison is first made from 1 to 3 and then from 3 to 8.

Of all the intervals, there are only three which are fundamental and which must consequently be remembered; these are the 3, the 5, and the 7, and we can arrange them in the following way. [Ex. III.3.] Each first note corresponds to 1, and its 3, its 5, and its 7 correspond to the numbers which designate these intervals. Once we know these three intervals with respect to that one of the seven notes taken as the first degree, we need only add the octave of this first degree in order to find that the third becomes the sixth, the fifth becomes the fourth, and the seventh becomes the second. These last three intervals, the sixth, the fourth, and the second, are thus inversions of the first and fundamental three.

Example III.3

This article must not be passed over too lightly, for the more we are convinced by our own experience of the truth advanced here, the easier we shall find it to understand the rest.

On the Staff, i.e., on the lines used to set down the Notes

The notes of music, whose names are already known to us, are represented by different symbols which mark their duration, and are placed on and between five lines arranged horizontally so that the degrees of the notes can be distinguished. [Ex. III.4.]

Example III.4

These five lines together are called the staff; each line in particular is called a line or a rule, and what is between the lines is called a middle or a space.

The lowest of these lines is the first, and consequently the highest is the fifth.

On Clefs

There are three clefs in music; here are their different symbols and the name of the note which each one designates. [Ex. III.5.]

Example III.5

The clef is always assumed to be on the line which crosses it, and this line takes the name of the clef. Only one clef at a time may be placed at the beginning of each staff, but another may be substituted for it when and where we desire, provided that it is placed on a line. The last clef always gives its name to the line which crosses it.

The Fa clef, which is the lowest of all, is generally placed on the fourth or on the third line. [Ex. III.6.]

Example III.6

The Do clef may be placed on any line except the fifth. The Do it designates should be a fifth above the Fa designated by the Fa clef. [Ex. III.7.]

Example III.7

The Sol clef is usually placed on the first or on the second line. This Sol is yet another fifth higher than the Do designated by the Do clef. [Ex. III.8.]

Example III.8

Since each clef gives its name to the line which crosses it, a note crossed by this same line should bear the name of the clef; thus the name of the clef is given both to the line and to the note. As we have not yet spoken about the shape of notes at all, those which we shall use in the meantime will be made like the capital O; some will be crossed by a line, while the others will be placed in the spaces. Thus, by counting according to the order of the scale from the note which takes the name of the clef, and by noticing that we ascend from the first line to the fifth, that we descend from the fifth to the first, and that the spaces as well as the lines take the names of notes, we cannot be misled. This should be studied in the following example. [Ex. III.9.]

Example III.9

Just as we have placed the first note on the line of the clef, we may place it likewise on or between any of the lines; to know the name of this note, we need only count from the clef.

Since it is absolutely necessary to know immediately the name of a note found on or between any lines, so as not to be occupied with such a trivial matter when the object is to compose, we should decide on a clef, placing it on an appropriate line, and learn by heart the names of the lines and the spaces with relation to this clef. For example, when the Fa clef is placed on the fourth line, we should be able to say immediately that the third line is called Re, the second Si, the first Mi [sic; this should be Sol], and the fifth La; that the...

Table of contents

• Title Page
• Copyright Page
• Dedication
• TRANSLATOR’S INTRODUCTION
• Table of Contents
• PREFACE
• TABLE OF TERMS
• BOOK ONE - On the Relationship between Harmonic Ratios and Proportions
• BOOK TWO - On the Nature and Properties of Chords and on Everything which may be used to make Music perfect
• BOOK THREE - Principles of Composition
• BOOK FOUR - Principles of Accompaniment