The Thirteen Books of the Elements, Vol. 2

Euclid

• Publisher: Dover Publications
• Year: 2012
• Print ISBN: 9780486600895
• eBook ISBN: 9780486158198
• Topic: Mathematics
• Subtopic: History & Philosophy of Mathematics
• Index: Mathematics

This is the definitive edition of one of the very greatest classics of all time — the full Euclid, not an abridgement. Using the text established by Heiberg, Sir Thomas Heath encompasses almost 2,500 years of mathematical and historical study upon Euclid.
This unabridged republication of the original enlarged edition contains the complete English text of all 13 books of the Elements, plus a critical apparatus that analyzes each definition, postulate, and proposition in great detail. It covers textual and linguistic matters; mathematical analyses of Euclid’s ideas; classical, medieval, Renaissance, modern commentators; refutations, supports, extrapolations, reinterpretations, and historical notes, all given with extensive quotes.
“The textbook that shall really replace Euclid has not yet been written and probably never will be.” — Encyclopaedia Britannica.
Volume 1. 151-page Introduction: life and other works of Euclid; Greek and Islamic commentators; surviving mss., scholia, translations; bases of Euclid’s thought. Books I and II of the Elements, straight lines, angles, intersection of lines, triangles, parallelograms, etc.
Volume 2. Books III-IX: Circles, tangents, segments, figures described around and within circles, rations, proportions, magnitudes, polygons, prime numbers, products, plane and solid numbers, series of rations, etc.
Volume 3. Books X to XIII: planes, solid angles, etc.; method of exhaustion in similar polygons within circles, pyramids, cones, cylinders, spheres, etc. Appendix: Books XIV, XV, sometimes ascribed to Euclid.

BOOK V.

INTRODUCTORY NOTE.

The anonymous author of a scholium to Books V. (Euclid, ed. Heiberg, Vol. V. p. 280), who is perhaps Proclus, tells us that “some say” this Book, containing the general theory of proportion which is equally applicable to geometry, arithmetic, music, and all mathematical science, “is the discovery of Eudoxus, the teacher of Plato.” Not that there had been no theory of proportion developed before his time; on the contrary, it is certain that the Pythagoreans had worked out such a theory with regard to numbers, by which must be understood commensurable and even whole numbers (a number being a “multitude made up of units,” as defined in Eucl. VII). Thus we are told that the Pythagoreans distinguished three sorts of means, the arithmetic, the geometric and the harmonic mean, the geometric mean being called proportion (ἀναλογία) par excellence; and further Iamblichus speaks of the “most perfect proportion consisting of four terms and specially called harmonic,” in other words, the proportion

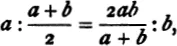
which was said to be a discovery of the Babylonians and to have been first introduced into Greece by Pythagoras (Iamblichus, Comm. on Nicomachus, p. 118). Now the principle of similitude is one which is presupposed by all the arts of design from their very beginnings; it was certainly known to the Egyptians, and it must certainly have been thoroughly familiar to Pythagoras and his school. This consideration, together with the evidence of the employment by him of the geometric proportion, makes it indubitable that the Pythagoreans used the theory of proportion, in the form in which it was known to them, i.e. as applicable to commensurables only, in their geometry. But the discovery, also by the Pythagoreans, of the incommensurable would of course be seen to render the proofs which depended on the theory of proportion as then understood inconclusive; as Tannery observes (La Géométrie grecque, p. 98), “the discovery of incommensurability must have caused a veritable logical scandal in geometry and, in order to avoid it, they were obliged to restrict as far as possible the use of the principle of similitude, pending the discovery of a means of establishing it on the basis of a theory of proportion independent of commensurability.” The glory of the latter discovery belongs then most probably to Eudoxus. Certain it is that the complete theory was already familiar to Aristotle, as we shall see later.

It seems probable, as indicated by Tannery (loc. cit) that the theory of proportions and the principle of similitude took, in the earliest Greek geometry, an earlier place than they do in Euclid, but that, in consequence of the discovery of the incommensurabl...

Table of contents

• Cover
• Title Page
• Copyright page
• Contents of Volume II
• Book III. Definitions.
• Book IV. Definitions.
• Book V. Introductory note.
• Book VI. Introductory note.
• Book VII. Definitions.
• Book VIII.
• Book IX.
• Greek Index to Vol. II.
• English Index to Vol. II.