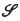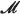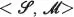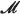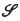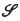Meaning, Quantification, Necessity

Themes in Philosophical Logic

Martin Davies

• Publisher: Routledge
• Year: 2019
• Print ISBN: 9781032808628
• eBook ISBN: 9781000735512
• Edition: 1
• Topic: Philosophy
• Subtopic: Business General

Originally published in 1981. This is a book for the final year undergraduate or first year graduate who intends to proceed with serious research in philosophical logic. It will be welcomed by both lecturers and students for its careful consideration of main themes ranging from Gricean accounts of meaning to two dimensional modal logic. The first part of the book is concerned with the nature of the semantic theorist's project, and particularly with the crucial concepts of meaning, truth, and semantic structure. The second and third parts deal with various constructions that are found in natural languages: names, quantifiers, definite descriptions, and modal operators. Throughout, while assuming some familiarity with philosophical logic and elementary formal logic, the text provides a clear exposition. It brings together related ideas, and in some places refines and improves upon existing accounts.

PART ONE

MEANING AND TRUTH

I

MEANING

1 THEORIES OF MEANING

The phrase ‘theory of meaning’ occupies a central place in philosophical logic. Yet that phrase is ambiguous. We need to distinguish:

(1) a (perhaps formalized) theory which, for some particular language L, yields a meaning specification for each well-formed sentence of L; that is, a theory which yields a theorem of the form

s means (in L) that p

for each sentence s of L;

(2) a (discursive) theory which illuminates the concept of meaning; that is, a philosophical account which analyses meaning in terms of other concepts, or at least reveals the location of the concept of meaning with respect to other concepts.

Concerning theories of meaning in the first sense (theories₁ of meaning), there are five brief preliminary points to be made. Someone might be concerned that, if a theory₁ of meaning for English is a theory which yields such theorems as

‘Everest is a mountain’ means (in English) that Everest is a mountain

then a theory₁ of meaning is something with an air of triviality about it. The first three points are intended to ease that worry, although the third also has a stipulative component.

(1) A theory₁ of meaning is a theory about a particular language, the object language (OL), and it is itself cast in a particular language, the metalanguage (ML). But what the theorems of the theory state in the ML about particular OL sentences could as readily be stated in any of a host of languages. What a Frenchman knows when he knows what the English sentence ‘Everest is a mountain’ means is just what an Englishman knows when he knows what that sentence means, although what a Frenchman would write down as part of a theory₁ of meaning for English would be a French sentence mentioning that English sentence and so would be different from what an Englishman would write down as part of a theory₁ of meaning for English.

(2) A theory₁ of meaning for one language cast in a second language is very different from a theory of translation for the first language into the second, even if the language in which the theory of translation is cast is itself the second language. We must contrast:

(i) ‘Kungen vet att Stockholm är en stor stad’ means (in Swedish) that the King knows that Stockholm is a large city;

(ii) ‘Kungen vet att Stockholm är en stor stad’ means (in Swedish) what ‘The King knows that Stockholm is a large city’ means (in English).

In (i) a certain English sentence is used in specifying the meaning of a Swedish sentence. In (ii) that same English sentence is mentioned as a sentence which means the same as the Swedish sentence. What obscures the difference is that, since the translation theory is cast in English as well as being a theory of translation into English, anyone who can read the theory probably knows what the mentioned English sentence means, and so can come to know what the Swedish sentence means. But the difference remains. What is stated by (i) is something knowledge of which itself suffices (e.g. in a Frenchman) for knowing what the Swedish sentence means. What is stated by (ii) is something knowledge of which does not itself so suffice (e.g. in a Frenchman). (On this point, see Lewis, 1972, pp. 169–70, and Evans and McDowell, 1976, pp. vii-xi.)

(3) The meaning specifications provided by a theory₁ of meaning for a language might or might not provide conceptual analyses of the meanings of sentences of that language. A theory₁ of meaning for Swedish in English might specify the meanings of Swedish sentences containing the present tensed verb ‘vet’ either by using the simple verb ‘knows’ or by using the phrase ‘has a justified true belief. Using the phrase to provide a conceptual analysis provides greater philosophical illumination, but that illumination is a contribution to epistemology rather than to philosophical logic. A meaning specification may be conceptually unilluminating, in this sense, without being trivial or empty. What is stated by a meaning specification which does not provide conceptual analysis, for a Swedish sentence containing ‘vet’, is something that most people do not know. It is not built into the notion of a theory₁ of meaning, as that notion is used here, that the theorems of such a theory should provide conceptual analyses. (We allow, in the terminology of Dummett, 1975, that a theory₁ of meaning may be modest rather than full-blooded.)

The fourth and fifth points are of an almost wholly stipulative character. The fourth is related to the topic of Chapter III. The full significance of the fifth will be seen in Chapter VIII.

(4) A theory₁ of meaning for a particular language L might have for each sentence of L an axiom specifying that sentence’s meaning. If L had infinitely many sentences then the theory would have infinitely many proper axioms (that is, infinitely many axioms other than those of the background logic of the theory). This would prevent a theorist from listing all the proper axioms, but it need not prevent him from specifying them. There might be an effectively recognizable feature such that the proper axioms are all and only the sentences of the ML which have that feature. In that case the proper axioms could be specified by a proper axiom schema. As we shall see (in Section III.l) there is a project which a theory₁ of meaning will not serve well if it simply has an axiom for each sentence of the OL. But it is not built into the notion of a theory₁ of meaning, as such, that it should have only finitely many proper axioms.

(5) A theory₁ of meaning for a particular language seems to state contingent facts about that language. It seems to be a merely contingent truth that ‘Det regnar’ means (in Swedish) that it is raining. Here we face a choice. We could regard a language as a changeable and indeed changing thing. In that case Swedish is a language which has the contingent property that in it, at present, ‘Det regnar’ means that it is raining. But let us instead regard a language as an unchanging and, indeed, unchangeable thing. It is a consequence of this stipulation that the language which is in fact at present spoken in Sweden has the non-contingent property that in it ‘Det regnar’ means that it is raining. A language in which those words did not mean that it is raining would be a different language. But we still have room for a contingent fact. It is a contingent fact that the people of Sweden speak a language in which ‘Det regnar’ means that it is raining. A quite different language could, if things had gone differently, have been spoken in that country./Ignoring for the moment both context dependence and ambiguity we could regard a language as an order pair

where

is a set of sentences and

is a set of meaning specifications, one for each sentence in

. If <

> = L and s is a sentence of

for which

specifies.

s means that p

then s is a sentence of L and s means (in L) that p (cf. Lewis, 1975, p. 3).

With the notion of a theory₁ of meaning thus clarified we must face a very natural question. How could any contribution be made to philosophical logic by attending to theories₁ of meaning for particular languages? For if one seeks to construct theories which provide conceptual analyses then one may contribute to philosophy but not specifically to philosophical logic, while if one seeks to construct theories which do not provide conceptual analyses then one may contribute, at best, to international relations or tourism.

One answer to this question is that a contribution can be made to philosophical logic by stating, quite generally, under what conditions a correct theory₁ of meaning for a language L is an adequate theory for the language of a given population G;that is, by stating under what conditions the language L is the actual language of G. (Let us ignore populations with bilingual members.) To state these conditions would be to provide a theory₂ of meaning, that is, a philosophical elucidation of the concept of meaning.

2 PROPOSITIONAL ATTITUDES AND ACTUAL LANGUAGES

The thought that elucidation of the concept of linguistic meaning (meaning in a language) must proceed via an account of what it is for members of a population to speak that language is a compelling one. It does not require us to deny that there are languages which no one speaks. It just requires us to deny that the significance of the claim that a certain sentence s means that p in a language L can be appreciated independently of any consideration of what it would be to speak L.

If members of a population G share a language L in which s means that p then those members can use utterances of s to express their belief that p. This claim is very rough, but refining it promises to yield us an account, employing the concepts of the propositional attitudes (belief, desire, intention, and so on), of what it is for L to be the actual language of G. That account will constitute a condition of adequacy upon any theory which purports to be a theory₁ of meaning for the language of G. Let us call any such condition of adequacy a propositional attitude constraint (PAC).

To see more clearly why there will be some such PAC which a theory must meet with respect to a population, if that theory is to be an adequate theory₁ of meaning for the language of that population (equivalently: if the language for which that theory is a correct theory₁ of meaning is to be the actual language of that population) imagine that a language L =

is spoken in a population G. Then the meaning specifications in

can contribute towards our interpretation of the utterances, by members of G, of (indicative) sentences in

and of sentences (in other moods) closely related to sentences in

; that is, towards our redescription of those utterances as linguistic acts of certain kinds (assertions, commands, questions, and so on) and with certain content...

Table of contents

• Cover
• Half Title
• Title Page
• Copyright Page
• Original Title Page
• Original Copyright Page
• Dedication
• Contents
• Preface
• Part One: Meaning and Truth
• Part Two: Quantification and Reference
• Part Three: Necessity and Actuality
• Appendices
• Bibliography
• Index