Topics in Modern Logic

D. C. Makinson

• Publisher: Routledge
• Year: 2019
• eBook ISBN: 9781000737066
• Edition: 1
• Topic: Philosophy
• Subtopic: Business General

Originally published in 1973. This book is directed to the student of philosophy whose background in mathematics is very limited. The author strikes a balance between material of a philosophical and a formal kind, and does this in a way that will bring out the intricate connections between the two. On the formal side, he gives particular care to provide the basic tools from set theory and arithmetic that are needed to study systems of logic, setting out completeness results for two, three, and four valued logic, explaining concepts such as freedom and bondage in quantificational logic, describing the intuitionistic conception of the logical operators, and setting out Zermelo's axiom system for set theory. On the philosophical side, he gives particular attention to such topics as the problem of entailment, the import of the Löwenheim-Skolem theorem, the expressive powers of quantificational logic, the ideas underlying intuitionistic logic, the nature of set theory, and the relationship between logic and set theory.

There are exercises within the text, set out alongside the theoretical ideas that they involve.

1 Some aspects of truth-functional logic

Outline

We begin by setting out an axiom system for the relation of tautological implication. We then give some examples of the derivation of theses in the axiom system, and digress to discuss the difference between working forwards and working backwards, both in the search for derivations and in problem solving in general. We describe some of the principal tools, drawn from arithmetic and the theory of sets, that are needed in the study of systems of logic. Finally, we use these tools to show that the axiom system is both sound and complete with respect to the relation of tautological implication.

1 An axiomatization of the relation of tautological implication

We shall assume that the reader has some acquaintance with the formulae of propositional logic. They are constructed from propositional letters p, q, r, … by means of operators such as negation, conjunction, disjunction, material implication, and material equivalence, which we shall write respectively as ⌉, ∧, ∨, ⊃ and ≡. We recall that of these operators, some are expressible in terms of others. For example we may take the operators ⌉, ∧, and ∨ as primitive and define the others in terms of them, considering α ⊃ ß as an abbreviation for, say, ⌉ (α ∧ ⌉ β) and regarding α ≡ ß as an abbreviation for (α ⊃ ß) ∧ (ß ⊃ α). Indeed, it is even possible to take the reduction further, but we shall find it convenient for some later developments to take all three of ⌉, ∧, and ∨ as primitive operators.

Exercise 1 Indicate two ways in which the reduction of primitive operators might be carried further.

We recall some of the fundamental definitions of truth-functional logic. A formula is said to be a tautology if it receives the value ‘true^’ for every assignment of truth values to its propositional letters. Here the word ‘iff’, which we shall use frequently, is merely a shorthand for ‘if and only if’. A formula is said to be a countertautology,or in the terminology of some authors a self contradiction, iff it receives the value ‘false’ for every assignment of truth values to its propositional letters. A formula is said to be contingent iff it is neither a tautology nor a countertautology. And finally, we say that one formula tautologically implies another iff there is no assignment of truth values to propositional letters upon which the first formula comes out true and the second comes out false.

Exercise 2 Let a be any formula. Verify that a is a tautology iff ⌉α is a countertautology. Also verify that α is contingent iff ⌉α is contingent.

Exercise 3 Let α and ß be formulae. Verify that α tautologically implies ß iff the formula α ⊃ ß is a tautology.

In this chapter we shall focus attention upon the relation of tautological implication. Our first problem will be a formal one: to axiomatize the relation. In other words we would like to pick out a few simple examples of tautological implication, and a few simple rules for generating new cases of tautological implication from old ones, in a way that will satisfy two conditions:

(1) Everything derivable from the chosen examples by means of the chosen rules really is a case of tautological implication;

(2) Every case of tautological implication can be derived, in a short or a long time, from the chosen axioms by means of the chosen rules.

Clearly, these two conditions are converses of each other. It is not obvious in advance that both objectives can be attained, but it turns out that in fact they can. Indeed there are many axiomatizations that do the job, and we shall choose the following one.

Some explanation is needed of the concept of an axiom scheme. Consider for example the first scheme, α ∧ ß → α. In setting this down we mean to indicate that infinitely many expressions of that form are counted as axioms. For every choice of formulae α and ß, the resulting expression covered by the scheme α ∨ ß → α is counted as an axiom. Thus if we choose α to be the propositional letter p and choose ß to be the formula q ∨ ⌉p, then the resulting expression p ∧ (q ∨ ⌉p) → p is an axiom, and is said to be an instance of the first axiom scheme. Again, if we choose a to be the formula q ∨ p, and choose ß to be the formula r ∧ s, then the resulting expression (q ∨ p) ∧ (r ∧ s) → q ∨ p is an axiom, and is also an instance of the first axiom scheme.

Exercise 4 List five further instances of the axiom scheme α ∧ ß → α. Find an expression that is simultaneously an instance of the axiom scheme α ∧ ß → α and an instance of the axiom scheme α ∧ ß → α. Find an expression that is simultaneously an instance of the axiom schemes α ∧ β → β and (α ∨ ß) ∧ ⌉α → β. Is there any expression that is simultaneously an instance of the schemes α ∧ ß → α and α → α ∨ β?

Each axiom contains a single arrow, flanked on left and right by formulae. This arrow should not be conflated with the hook sign. The hook is used as an operator, building formulae out of formulae, and is understood as representing material implication. The arrow is being used to represent a certain relation between formulae which, we shall show, coincides with tautological implication.

Each axiom scheme and derivation rule is a well known personality in logical life. The topmost schemes tell us that a conjunction implies each of its conjuncts, and that a disjunction is implied by each of its disjuncts. Next we have the principles of double negation. The next line gives us one of the principles of distribution, telling us that conjunction may be distributed over disjunction. Note that the converse principle

has not been included in the list of axiom schemes, nor have the two dual principles

There is nothing objectionable about these distribution principles, and they all correspond to genuine tautological implications. But if we take only our given distribution principle from among them as an axiom scheme, then the remainder can all be derived using the derivation rules.

The final axiom scheme, (α ∨ β) ∧ ⌉ α → ß is known as the principle of disjunctive syllogism. It is rather inconspicuous, but as we shall later see, leads to some curious results.

The derivation rules also express familiar principles. The first lays down the transitivity of the implication relation. The second authorizes conjoining the consequents of a single antecedent, whilst dually the third authorizes disjoining the antecedents of a single consequent. The final derivation rule expresses the principle of contraposition. The basic difference between the axiom schemes and the derivation...

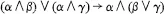
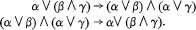
Table of contents

• Cover
• Half Title
• Title Page
• Copyright Page
• Original Title Page
• Original Copyright Page
• Contents
• Preface
• 1 Some aspects of truth-functional logic
• 2 Some modified implication relations
• 3 Some aspects of quantificational logic
• 4 Remarks on the intuitionistic approach to logic
• 5 From logic to set theory
• Answers to selected exercises
• Guide to further reading
• Index