Introduction to the Theory of Formal Groups

Jean A. Dieudonne

• Publisher: CRC Press
• Year: 2020
• ISBN:
  9781000723311
• Edition: 1
• Topic: Matemáticas
• Subtopic: Matemáticas general

The concept of formal Lie group was derived in a natural way from classical Lie theory by S. Bochner in 1946, for fields of characteristic 0. Its study over fields of characteristic p > 0 began in the early 1950's, when it was realized, through the work of Chevalley, that the familiar "dictionary" between Lie groups and Lie algebras completely broke down for Lie algebras of algebraic groups over such a field. This volume, starts with the concept of C-group for any category C (with products and final object), but the author's do not exploit it in its full generality. The book is meant to be introductory to the theory, and therefore the necessary background to its minimum possible level is minimised: no algebraic geometry and very little commutative algebra is required in chapters I to III, and the algebraic geometry used in chapter IV is limited to the Serre- Chevalley type (varieties over an algebraically closed field).

CHAPTER I

Definition of Formal Groups

§1. C-groups and C-cogroups

1. The notion of C-group. Let C be a category which has a final object e and in which the product of any two objects is defined. A C-group consists in a quadruplet (G, m, η, i) where G is an object of C, m: G × G → G, η : e → G, and i: G → G three morphisms of C, with the following axioms:

1) The diagram

is commutative.

2) The two diagrams

are commutative (the oblique arrow is the natural isomorphism).

3) The two diagrams

are commutative.

When one takes as C the category of sets, the morphisms being arbitrary mappings, one obtains the usual definition of groups (also called “abstract” or “set-theoretic” groups). When one takes for C the category of topological spaces, the morphisms being continuous mappings, one obtains the topological groups (in that category, products are just the usual products of topological spaces, and the final object a space having only one point).

2. It is well-known that there is another way of defining C-groups. For each object X in C, consider the set of morphisms Mor(X, G) (or Mor_c(X, G)) of all morphisms (of C) of X into G; the mapping X ⟼ Mor(X, G) is a functor from the dual category C⁰ of C into the category of sets: to each morphism u: X → X′ in C is associated the mapping f ⟼ f ∘ u of Mor(X′, G) into Mor(X, G). This is valid for an arbitrary object Gin C, but if G is a C-group, it is possible to define on Mor(X, G) a group structure in a natural way, such that, for any morphism u: X → X′, the mapping f ⟼ f ∘ u of Mor(X′, G) into Mor(X, G) is a group homomorphism. To define the group law on Mor(X, G), observe that

$\text{Mor(X, G)}\text{× Mor(X, G)}$

is naturally identified with Mor(X, G × G) by definition of the product in C; the group law is then simply

${\mu }_{\text{X}}(f\text{,}g\text{)}\mapsto m\circ (f\text{,}g\text{)}\text{.}$

The associativity results from property 1); the neutral element is just the composite morphism ${\epsilon }_{\text{x}}\text{:X}\to e\stackrel{\eta }{\to }\text{G}\eta$, the fact that it is a neutral element following from property 2); finally the inverse is the mapping f ⟼ i ∘ f, its properties following from property 3). We may thus say that a C-group G defines in a natural way a functor X ⟼ Mor(X, G) from C⁰ to the category of (abstract) groups Gr.

3. Conversely, if an object G of C is such that X ↦ Mor (X, G) is a functor from C⁰ to Gr, then there is a unique ...

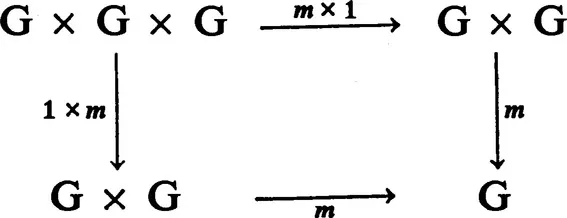
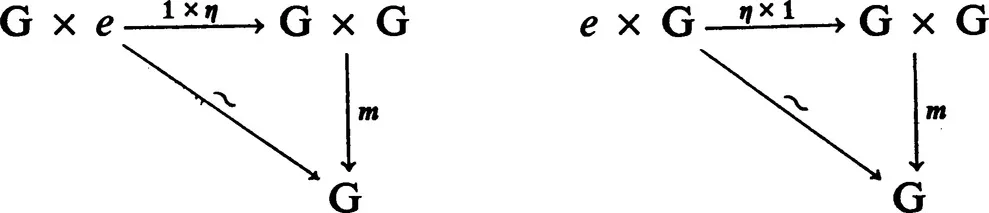
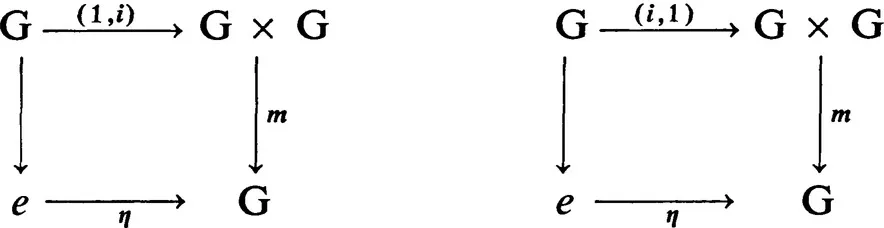
Table of contents

• Cover
• Half Title
• Pure and Applied Mathematics
• Title Page
• Copyright Page
• Table of Contents
• Foreword
• Notations
• Original Half Title
• Chapter I Definition of Formal Groups
• Chapter II Infinitesimal Formal Groups
• Chapter III Infinitesimal Commutative Groups
• Chapter IV Representable Reduced Infinitesimal Groups
• Bibliography
• Index