Multiobjective Optimization Methodology

A Jumping Gene Approach

K.S. Tang, T.M. Chan, R.J. Yin, K.F. Man

• Publisher: CRC Press
• Year: 2018
• Print ISBN: 9781439899199
• eBook ISBN: 9781351832526
• Edition: 1
• Topic: Biological Sciences
• Subtopic: Electrical Engineering & Telecommunications
• Index: Biological Sciences

The first book to focus on jumping genes outside bioscience and medicine, Multiobjective Optimization Methodology: A Jumping Gene Approach introduces jumping gene algorithms designed to supply adequate, viable solutions to multiobjective problems quickly and with low computational cost.

Better Convergence and a Wider Spread of Nondominated Solutions

The book begins with a thorough review of state-of-the-art multiobjective optimization techniques. For readers who may not be familiar with the bioscience behind the jumping gene, it then outlines the basic biological gene transposition process and explains the translation of the copy-and-paste and cut-and-paste operations into a computable language.

To justify the scientific standing of the jumping genes algorithms, the book provides rigorous mathematical derivations of the jumping genes operations based on schema theory. It also discusses a number of convergence and diversity performance metrics for measuring the usefulness of the algorithms.

Practical Applications of Jumping Gene Algorithms

Three practical engineering applications showcase the effectiveness of the jumping gene algorithms in terms of the crucial trade-off between convergence and diversity. The examples deal with the placement of radio-to-fiber repeaters in wireless local-loop systems, the management of resources in WCDMA systems, and the placement of base stations in wireless local-area networks.

Offering insight into multiobjective optimization, the authors show how jumping gene algorithms are a useful addition to existing evolutionary algorithms, particularly to obtain quick convergence solutions and solutions to outliers.

1

Introduction

1.1 Background on Genetic Algorithms

The genetic algorithm (GA) was first proposed by John Holland [30] in the late 1960s. As a major family in evolutionary algorithms, it was inspired by the natural phenomenon of biological evolution, relying on the principle of “survival of the fittest.” The basic flowchart of a conventional GA is given in Figure 1.1. A GA process begins with a random population in which potential solutions are encoded into chromosomes. By evaluating each chromosome against the objective functions, its goodness, represented by a fitness value, can be determined. Based on the fitness value, some chromosomes are then selected to form a mating pool that will undergo genetic operations, namely, crossover and mutation, to produce some new solutions. The chromosomes (called the parents) in the mating pool exchange their genes to generate new chromosomes via crossover, while some genes are changed by a random process called mutation. These two operations keep the balance between the exploration and exploitation of solutions so that a GA can form better solutions based on acquired information and some random processes. The newly formed chromosomes are then assessed by objective functions, and fitness values are assigned. Usually, fitter offspring will replace some or all of the old ones such that a new population is obtained. This genetic cycle is repeated until some criteria are met. Further operational details of GA can be found in [41].

After about 30 years of development worldwide, the GA has been successfully applied to various real-world applications [3]. These areas include physics, chemistry, engineering, medicine, business and management, finance and trade, and more. Table 1.1 presents a summary of the work. This list is by no means exhaustive, but it should provide an impression of how GAs have influenced the scientific world through research and applications.

According to the nature of the problems, these applications can also be classified as single- or multiple-objective optimization. For single-objective optimization, only one objective is targeted, while there are several in multiobjective optimization. A unique global solution is commonly expected in the former, but a set of global solutions should result from the latter.

FIGURE 1.1
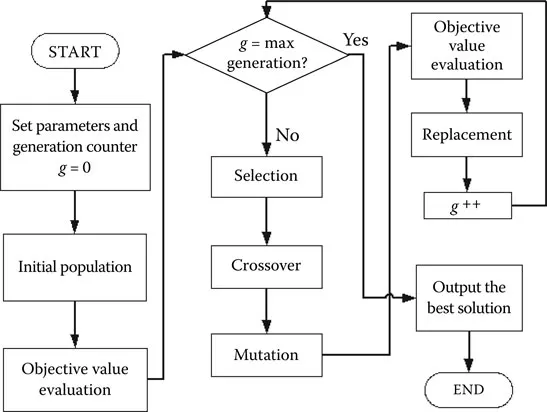
Genetic cycle of a GA. (From Yin, J.J., Tang, K. S., Man, K. F., A comparison of optimization algorithms for biological neural network identification, IEEE Transactions on Industrial Electronics, 57(3), 1127–1131, 2010.)

TABLE 1.1

Typical Applications of GA in Different Research Areas

Research Area	Examples of Applications
Physics	Water reactor [49]; two-nucleon knockout reactions [32]; Tokamak poloidal field configuration [2]; four-level triplicator [6]; spectrum assignment [51]
Chemistry	Biological activity of combinatorial compound libraries [52]; catalytic reaction sets [39]; molecule conformational search [35]; modeling of response surfaces in high-performance liquid chromatography [47]; structure elucidation of molecules [46]
Engineering	Network design [38]; city planning [4]; aerodynamic design [48]; filter design [43]; path planning for underwater robot [1]
Medicine	Allocation of radiological worker [8]; medical imaging [28]; treatment planning [9]; classification of traditional Chinese medicine [54]; medical diagnosis [45]
Business and management	Personnel scheduling [19]; forest management [23]; job shop scheduling [33]; unit commitment [14]; distribution [7]
Finance and trading	Performance prediction for individual stock [40]; financial time series [50]; economic models [42]; investment strategies [34]; trade strategies [31]

By transforming multiple objectives into a single fitness value, as a population-based optimization algorithm, the GA is especially effective for solving multiobjective optimization problems (MOPs) [25,26]. A number of multiobjective evolutionary algorithms (MOEAs) have been proposed, including the multiobjective genetic algorithm (MOGA) [25]; niched Pareto genetic algorithm 2 (NPGA2) [20]; nondominated sorting genetic algorithm 2 (NSGA2) [17,18]; strength Pareto evolutionary algorithm 2 (SPEA2) [55]; Pareto archived evolution strategy (PAES) [36,37]; microgenetic algorithm (MICROGA) [11,12]; and so on.

Except for the PAES, all of these MOEAs are GA based, and they rely on Pareto sampling techniques, which are capable of generating multiple solutions in a single simulation run. However, true Pareto-optimal solutions are seldom reached by MOEAs. A set of nondominated solutions is thus obtained instead [10,16], and this solution set is preferably as close to the true Pareto-optimal front or reference front [10] as possible. Then, selecting a compromising solution for a particular application is the responsibility of the decision maker.

Although advanced developments of various MOEAs together with many additional measures have been suggested (e.g., mating restrictions [5,21,22,29,30], fitness sharing [27], and the crowding scheme [15]), it is still not an easy task to obtain a widespread nondominated solution set, and the convergence speed is usually slow. Thus, another biological genetic phenomenon is considered as a possible way to improve search performance for evolutionary computation, which is also the focus of this book.

When evolution proceeds generation by generation in an MOEA, the genes in the chromosomes of the parent are passed to the offspring. This is called vertical gene transmission (VGT). In the early period, it was thought that all genes in chromosomes were fixed and could be transferred only through the VGT process. Nevertheless, this was not true; biologist Barbara McClintock first discovered that some kinds of genes could “jump” horizontally in the same chromosome or to other chromosomes in the same generation when there was stress exerted on the chromosomes [13,24,44]. Therefore, these genes were called jumping genes (JGs); this phenomenon was termed horizontal gene transmission (HGT).

The framework of an MOEA provides a unique platform for the imitation of the JG as each fitness function can affect a certain part (genes) of the chromosomes throughout the evolutionary process. The striking findings of the JG are that it not only offers better convergence but also presents a wider spread of nondominated solutions, especially at both ends of the true Pareto-optimal front

This book thus serves as a key reference for the introduction of the JG in evolutionary computation, covering the fundamental concept, theoretical justification, simulation verifications, and applications of the JG.

1.2 Organization of Chapters

This book has nine chapters, including the introduction in this chapter. In Chapter 2, a thorough review of state-of-the-art multiobjective optimization techniques is presented. This leads the way for new development of evolutionary theory such as JG to further unravel the shortfall of multiobjective optimization, particularly when convergence and diversity are both in demand.

Considering the fact that the biogenetic phenomenon of the JG may be new to readers, the basic biological gene transposition process is described in Chapter 3. It serves as a shortcut to the bioscience for comprehension of the JG concept. The transformation of gene manipulation in the computational forms, namely, copy and paste and cut and paste, is then presented, supported by a series of studies on its suitability.

As the JG is such a new algorithm, it is preferable to derive the necessary proofs of the JG mathematically at the beginning. A number of theoretical proposals in this endeavor have been under consideration, but it was the schema theory deployed by Stephens and Waelbroeck’s model that became the winner. Chapter 4 provides an exact mathematical formulation for the growth of the schemata; consequently, two delightful mathematical equations, one for the copy-and-paste and the other for the cut-and-paste operations are established and presented. Further efforts to derive important theories for understanding the dynamics of t...

Table of contents

• Cover
• Half Title
• Title Page
• Copyright Page
• Table of Contents
• Preface
• About the Authors
• 1. Introduction
• 2. Overview of Multiobjective Optimization
• 3. Jumping Gene Computational Approach
• 4. Theoretical Analysis of Jumping Gene Operations
• 5. Performance Measures on Jumping Gene
• 6. Radio-to-Fiber Repeater Placement in Wireless Local-Loop Systems
• 7. Resource Management in WCDMA
• 8. Base Station Placement in WLANs
• 9. Conclusions
• Appendix A: Proofs of Lemmas in Chapter 4
• Appendix B: Benchmark Test Functions
• Appendix C: Chromosome Representation
• Appendix D: Design of the Fuzzy PID Controller
• Index