Molecular Dynamics Simulation of Nanostructured Materials

An Understanding of Mechanical Behavior

Snehanshu Pal, Bankim Chandra Ray

• Publisher: CRC Press
• Year: 2020
• Print ISBN: 9781032728773
• eBook ISBN: 9780429670961
• Topic: Mathematics
• Subtopic: Mathematics General
• Index: Mathematics

Molecular dynamics simulation is a significant technique to gain insight into the mechanical behavior of nanostructured (NS) materials and associated underlying deformation mechanisms at the atomic scale. The purpose of this book is to detect and correlate critically current achievements and properly assess the state of the art in the mechanical behavior study of NS material in the perspective of the atomic scale simulation of the deformation process. More precisely, the book aims to provide representative examples of mechanical behavior studies carried out using molecular dynamics simulations, which provide contributory research findings toward progress in the field of NS material technology.

1	Structural Description of Materials

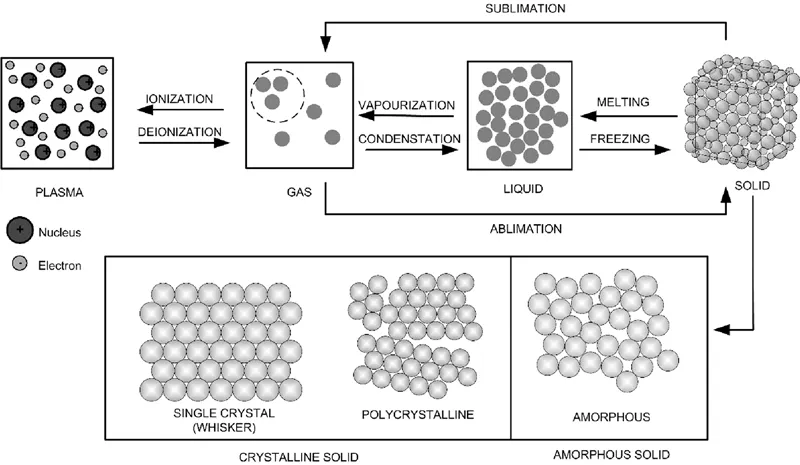
1.1 ATOMIC ARRANGEMENTS IN MATERIALS

Materials are made up of atoms, molecules, and ions present in different states such as gas, liquid, and solid. According to the kinetic molecular theory, the atoms/molecules in solids vibrate and rotate at their respective places instead of moving. Solids have stronger attractive forces to hold molecules/atoms in contrast to liquids and gases. Solids acquire definite shapes and volumes and can also withstand some amount of shear forces without undergoing any deformation. Furthermore, solids can be broadly classified into two major categories, crystalline solids and amorphous solids, which are shown in Figure 1.1. In crystalline solids, the atoms, ions, or molecules are arranged in a regular, well-defined periodic manner. In amorphous solids, the arrangement of atoms, ions, or molecules is disordered, with lacking periodicity.

Crystalline solids can be divided into following four categories based on the types of particles (atom/ion/molecule) present and the types of bonding between the particles:

1. Ionic solids

2. Metallic solids

3. Covalent network solids

4. Molecular solids

The constituent particles, type of effective binding forces, and properties of different crystalline solids along with examples are presented in Table 1.1.

1.1.1 PERIODICITY IN CRYSTALS AND SYMMETRY ELEMENTS

The basic difference between crystals and non-crystals is that atomic arrangement in crystals is in the form of a periodic array in a space. Such kind of periodic array constitutes a three-dimensional (3D) representative unit of a structure, where a group of atoms/molecules is repeated after regular intervals. Such a 3D array of points having identical surroundings may be defined as space lattice. If the periodicity in the structure along a line is a₁, then position of any lattice point along the line can be identified by a translation operation, r_u = ua₁. In case of two-dimensional (2D) and 3D arrangements, similarly, r_uv = ua₁ + va₂ and r_uvw = ua₁ + va₂ + wa₃ will be translational vectors, respectively, where u, v, and w are the integers. Figure 1.2a,b,c illustrates 2D and 3D cubic lattices. Unit cell is the smallest unit of volume that permits identical cells to be stacked together in a lattice space; therefore, the entire crystal lattice can be created by repeating the pattern of the unit cell over and over in all directions. If a unit cell is constructed without any overlap with another unit cell and is also free from any kind of defect, then it is called a primitive unit cell. A body is considered to be symmetrical when it is reproduced by certain symmetry operations such as translation, rotation, reflection, and inversion.

FIGURE 1.1 Transformation and reverse transformation between various states of matter with the application of heating or cooling.

TABLE 1.1
Categories of Solids and Their Salient Features

Type of Solid	Form of Unit Particles	Forces Between Particles	Solubility	Examples
Molecular	Atoms or molecules	London dispersion forces, dipole-dipole forces, hydrogen bonds	Depends on the polarity of the molecules	Argon (Ar), methane (CH4), sucrose (C12H22O11), dry ice (CO2)
Covalent network	Atoms connected in a network of covalent bonds	Covalent bonds	Insoluble in all solvents	Diamond (C) and quartz (SiO2)
Ionic	Positive and negative ions	Electrostatic attractions	Soluble in polar solvents	Typical salts such as NaCl and Ca(NO3)2
Metallic	Atoms	Metallic bonds	Insoluble in all solvents	All metallic elements: Cu, Fe, Al, Pt, etc

FIGURE 1.2 (a) and (c) are examples of two-dimensional lattices, indicating several possible sets of primitive basis vectors. (b) shows three-dimensional cubic lattices.

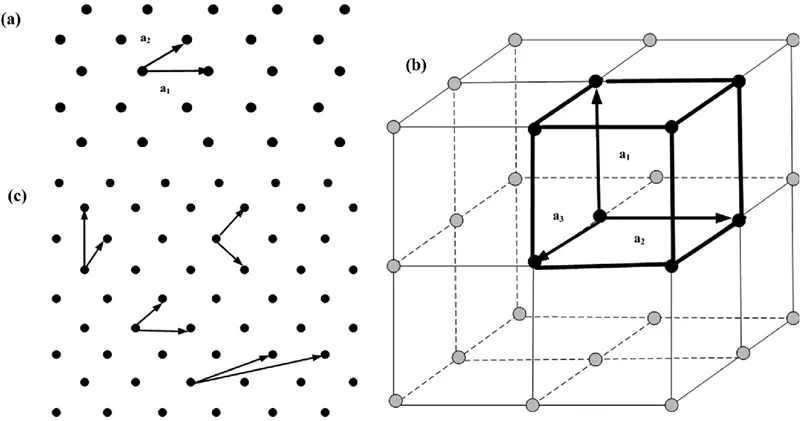
1.1.2 CRYSTAL LATTICES AND STRUCTURES

There are numerous ways in which the atoms can be arranged periodically in different lattices. These are known as the Bravais lattices. The combination of lattice (how to repeat) and motif (what to repeat) constitutes the crystal structure. A perfect crystal is the one in which all its lattice points are occupied by atoms, without any defects. However, such a scenario is not practically possible, as defects exist in the materials. In entirety, there are 7 crystal systems and 14 unique and non-repeating Bravais lattices, which are listed in Table 1.2.

TABLE 1.2
The Seven-Crystal Structures and Their Structural Features

Sl. No.	Crystal System	Relation Between the Sides	Relation Between the Angles	Bravais Lattices, Number and Types
1.	Cubic	a = b = c	α = β = γ = 90°	3 = S, BC, FC
2.	Tetragonal	a = b ≠ c	α = β = γ = 90°	2 = S, BC
3.	Hexagonal	a = b ≠ c	α = β = 90°, γ = 120°	1 = S
4.	Orthorhombic	a ≠ b ≠ c	α = β = γ = 90°	4 = S, BC, FC, EC
5.	Rhombohedral	a = b = c	α = β = γ ≠ 90°	1 = S
6.	Monoclinic	a ≠ b ≠ c	α = β = 90°, γ ≠ 120°	2 = S, EC
7.	Triclinic	a ≠ b ≠ c	α ≠ β ≠ γ ≠ 90°	1 = S

S: simple, BC: body center, FC: face center, EC: end center.

The most common primitive unit cells include Wigner-Seitz cell. The construction of the Wigner-Seitz cell is as follows [1]:

• Draw lines in order to connect a lattice point to all its neighboring points present in the lattice.

• Bisect each constructed line with a plane normal to this line, as presented in Figure 1.3a.

• The Wigner-Seitz cell is the smallest polyhedron bound by these planes. Figure 1.3b illustrates the Wigner-Seitz cell for a body-centered cubic Bravais lattice, where square and hexagonal faces can be seen.

Based on the symmetry considerations, 2D Bravais lattices can be classified into five categories. The most common lowest symmetry lattice includes the oblique lattice, which is invariant when rotated at an angle of π. There are four special lattice types that are invariant under numerous rotations and reflection symmetry operators. The constraints on the unit cell axes and angles for the aforementioned special lattice types are listed in Figure 1.3c, for example, monolayer materials such as graphene and boron. They may be quite large and contain many unit cells (quasi-infinite), or they may be of finite size or long ribbons of a nanoscale width.

Considering symmetry, 3D Bravais lattices can be assorted into 14 types. They are classified into seven types of unit cells based on their restrictions on the unit cell axes and angles for each of the 3D Bravais lattice types. For example, the cubic lattice includes simple cubic, body-centered cubic, and face-centered cubic. Here, the triclinic lattice is the most common, and there are 13 more special lattice types.

FIGUR...

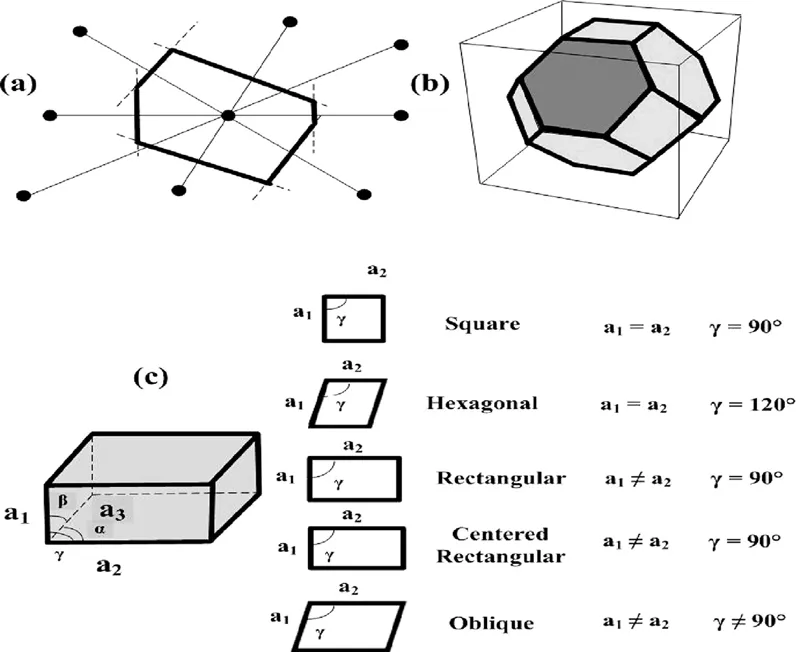
Table of contents

• Cover
• Half Title
• Title Page
• Copyright Page
• Dedication
• Table of Contents
• Preface
• Authors
• Chapter 1 Structural Description of Materials
• Chapter 2 Mechanical Behavior of Materials
• Chapter 3 Creep and Fatigue Behavior of Materials
• Chapter 4 Mechanical Behavior of Nanostructured Materials
• Chapter 5 Basics of Molecular Dynamics Simulation
• Chapter 6 Stress-Strain Behavior Investigation by Molecular Dynamic (MD) Simulation
• Chapter 7 Fracture Simulations Using Molecular Dynamics (MD)
• Chapter 8 Creep Behavior Investigation by Molecular Dynamics (MD) Simulation
• Chapter 9 Fatigue Behavior Investigation by Molecular Dynamics (MD) Simulation
• Index