Nonlinear Dynamics

A Two-Way Trip from Physics to Math

H.G Solari

• Publisher: Routledge
• Year: 2019
• ISBN:
  9781351428293
• Edition: 1
• Topic: Mathématiques
• Subtopic: Programmation linéaire et non linéaire

Nonlinear Dynamics: A Two-Way Trip from Physics to Math provides readers with the mathematical tools of nonlinear dynamics to tackle problems in all areas of physics. The selection of topics emphasizes bifurcation theory and topological analysis of dynamical systems. The book includes real-life problems and experiments as well as exercises and work

Chapter 1

Nonlinear dynamics in nature

‘man never regards what he possesses as so much his own, as what he does; and the labourer who tends a garden is perhaps in a truer sense its owner, than the listless voluptuary who enjoys its fruits… In view of this consideration, it seems as if all peasants and craftsmen might be elevated into artists; that is, men who love their labour for its own sake, improve it by their own plastic genius and inventive skill, and thereby cultivate their intellect, ennoble their character, and exalt and refine their pleasures. And so humanity would be ennobled by the very things which now, though beautiful in themselves, so often serve to degrade it… But, still freedom is undoubtedly the indispensable condition, without which even the pursuits most congenial to individual human nature can never succeed in producing such salutary influences. Whatever does not spring from a man’s free choice, or is only the result of instruction and guidance, does not enter into his very being, but remains alien to his true nature; he does not perform it with truly human energies, but merely with mechanical exactness… we admire what he does, but despise what he is.’

Wilhelm Von Humboldt [chom87]

A sound theory starts usually with experiment. The cornerstone of natural sciences is precisely its validation procedure, namely the fact that relevant assertions can be put to test by way of suitable experiments and eventually be rejected (if the experiment proves them wrong). Consequently, the aim of this chapter is to present nonlinear problems from the experimental point of view. By nonlinear we just mean systems that demand to be modelled by nonlinear differential equations or nonlinear discrete-time mappings.

We will review some experiments that illustrate the kind of phenomenon we expect to find in nonlinear systems. The choice of examples is unavoidably biased and incomplete. We combine everyday experiences with well known problems, all of them sharing the characteristic features of nonlinearity. We want to emphasize that for the physicist nonlinear dynamics is far more than a theoretical entertainment. Moreover, we hope to make clear that almost everything in nature is nonlinear.

1.1 Hiking among rabbits

A few years ago one of us went to a National Park near Ushuaia, Argentina on a 2 week hiking trip. The park is placed in the southernmost part of Tierra del Fuego, the mysterious island that enchanted sailors, poets and natural scientists [darw88]. At that time, it was striking to notice that there were plenty of rabbits, and that many of them looked rather ill.

In fact, rabbits are not ‘original’ to the place, but were introduced (from Europe) by sailors as a way of having fresh meat when the ports of Tierra del Fuego were a natural stop in the route from the Atlantic to the Pacific, before the opening of the Panama Canal. Rabbits reproduced and spread all around the region (which suggests that they encountered no natural predators).

Towards the end of the 19th century the region was substantially occupied by cattle-farmers. Rabbits entered into competition with the cattle (sheep) and the farmers searched for a way of getting rid of them.

The farmers learned that a similar situation had arisen in Australia, where the matter was ‘solved’ by inoculating rabbits with a specific virus, which provoked a dramatic decrease in their population. The same approach was tried in Tierra del Fuego despite the opposition of the Park authorities and rangers. The inoculation was not as massive as in Australia, since the Park became virtually a protection sanctuary and the farmers did not find collaboration for their project.

After a sharp drop in population, rabbits in Australia recovered their previous population levels, developing a virus-resistant breed. In Argentina, after an initial decrease in population, a fluctuating state has been reached. There is an apparently periodic alternation between years with high levels of mortality and sickness and years with low levels of mortality.

The tale has many morals. However, we will concentrate on some physically relevant consequences, although they may not be the most important. To begin with we shall assume that the comparison between the Australian and the Argentine ‘experiments’ is scientifically valid.

To assess which are the reasons behind oscillatory behaviour in population dynamics is an interesting topic of research in itself. For our purposes, one would expect that periodic changes in rabbit populations would have a ‘natural’ period such as that of the season cycle or the reproduction cycle.

We begin noticing that seemingly similar systems (rabbit populations) starting from apparently different initial states (the ratio between infected and healthy rabbits) can lead to the occurrence of different final (asymptotic) states. This result may not be surprising recalling better known problems such as the ideal pendulum or a two-body Kepler problem.

The dramatically new result is the existence of oscillating cycles which extend over several years. What is surprising is not the periodic character of the solution but rather the fact that the period is not the ‘natural’ one. A recurrence of many times a given period is called suhharmonic behaviour. Such behaviour cannot be achieved within a linear model.

Population dynamics, epidemiology and mathematical biology in general count among the most important contributors to the ‘comeback’ experienced by nonlinear science in recent decades. For example, very important names associated with nonlinear dynamics such as S Smale [smal76] and R May [may 75] have worked on this subject. A discussion concerning the example of the rabbits can be found in [dwye90]. Needless to say, the example of the rabbits is far from being unique.

1.2 Turbulence

The 1883 paper by Osborne Reynolds [reyn83] established the law of similarity that now bears his name (recall the Reynolds number). The article was concerned with two issues, one practical and one philosophical: ‘the law of resistance of the motion of water in pipes’ and ‘that the general character of the motion of fluids in contact with solid surfaces depends on the relation between a physical constant of the fluid and the product of the linear dimensions of the space occupied by the fluid and the velocity’. Discussing these issues, Reynolds gave us the first study of the transition from laminar motion to turbulent motion in a fluid (direct and sinuous motion, as they are called in the paper). The exposition hardly needs further comments.

Reynolds states that ‘The internal motion of water assumes one or another of two broadly distinguishable forms — either the elements of the fluid follow one another along the lines of motion which lead in the most direct manner to their destination, or they eddy about in sinuous paths the most indirect possible’. These are the laminar and turbulent forms of motion.

Further, we read that ‘Certain circumstances have been definitely associated with the particular laws of force. Resistance, [varying] as the square of the velocity, is associated with motion in tubes of more than capillary dimensions, and with the motion of bodies through the water at more than insensibly small velocities, while resistance [varying] as the velocity is associated with capillary tubes and small velocities’. This is illustrated by figure 1.1 taken from Prandtl and Tietjens [pran34].

There are other circumstances that distinguish turbulent motion from laminar motion. For example, while laminar motion does not mix different stream lines, turbulent motion does. Therefore, if we colour one of the streamlines (see figure 1.2 taken from [reyn83]), or heat it up as in [barn04], only this streamline will be altered while, by contrast, in turbulent motion the whole fluid downstream of the alteration will be changed. Reynolds’ description of this experiment is an excellent piece of scientific literature.

Having established that the transition between laminar and turbulent flow was likely to depend on the dimensionless quantity R = dUr/v (d = density, U = velocity, r = radius of the tube and υ = viscosity. R is now called the Reynolds number), Reynolds studied the transition for different tubes at different temperatures and established the following facts:

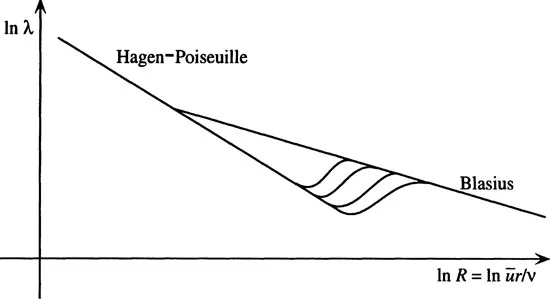
Figure 1.1. Resistance to motion in tubes against Reynolds number. Linear relation for laminar flow and quadratic relation for turbulent flows (from Prandtl and Tietjens, figure 17. See text).

(a) The transition depends on the initial disturban...