Discrete Mathematics

Graph Algorithms, Algebraic Structures, Coding Theory, and Cryptography

Sriraman Sridharan, R. Balakrishnan

• Publisher: Chapman and Hall/CRC
• Year: 2019
• Print ISBN: 9780815347392
• eBook ISBN: 9780429942624
• Edition: 1
• Topic: Mathematics
• Subtopic: Applied Mathematics
• Index: Mathematics

Conveying ideas in a user-friendly style, this book has been designed for a course in Applied Algebra. The book covers graph algorithms, basic algebraic structures, coding theory and cryptography. It will be most suited for senior undergraduates and beginning graduate students in mathematics and computer science as also to
individuals who want to have a knowledge of the below-mentioned topics.

• Provides a complete discussion on several graph algorithms such as Prims algorithm and Kruskals algorithm for sending a minimum cost spanning tree in a weighted graph, Dijkstras single source shortest path algorithm, Floyds algorithm, Warshalls algorithm, Kuhn-Munkres Algorithm. In addition to DFS and BFS search, several applications of DFS and BFS are also discussed.
• Presents a good introduction to the basic algebraic structures, namely, matrices, groups, rings, fields including finite fields as also a discussion on vector spaces and linear equations and their solutions.
• Provides an introduction to linear codes including cyclic codes.

Presents a description of private key cryptosystems as also a discussion on public key cryptosystems such as RSA, ElGamal and Miller-Rabin. Finally, the Agrawal-KayalSaxena algorithm (AKS Algorithm) for testing if a given
positive integer is prime or not in polynomial time is presented- the first time in a textbook.

Two distinguished features of the book are:

• Illustrative examples have been presented throughout the book to make the readers appreciate the concepts described.
• Answers to all even-numbered exercises in all the chapters are given.
  

Chapter 1

Graph Algorithms I

The aim of physical sciences is not the provision of pictures, but the discovery of laws governing the phenomena and the application of these laws to discover new phenomena. If a picture exists, so much the better. Whether a picture exists or not is only a matter of secondary importance.

P. Dirac

In this chapter, we study various algorithms on graphs. Unfortunately, the graphs are not manipulated by their geometrical representation inside a computer. We start with two important representations of graphs: the adjacency matrix representation and the adjacency list representation. Of course, we have to choose a representation so that the operations of our algorithm can be performed in order to minimize the number of elementary operations.

After seeing how the graphs are represented inside a computer, two minimum spanning tree algorithms in a connected simple graph with weights associated to each edge, one due to Prim and the other invented by Kruskal are presented. Then, shortest path problems in a weighted directed graph are studied. First, the single-source shortest path problem due to Dijkstra is presented. As an application, an algorithm is given to test the bipartiteness of a graph. Next, a single-source shortest path algorithm for negative edge weights is given. Then, all-pairs shortest path problem due to Floyd and the transitive closure algorithm by Warshall are given. Floyd’s algorithm is applied to find eccentricities of vertices, radius and diameter of a graph.

Finally, we study a well-known graph traversal technique, called depth-first search. As applications of the graph traversal method, we study the algorithms to find connected components, biconnected components, strongly connected components, topological sort and program evaluation and research technique (PERT). In the last subsection, we study the famous NP-complete problem, traveling salesman problem (TSP) and present the brute-force algorithm and two approximate algorithms. For basic properties of graphs and digraphs, the reader may see [6].

1.1Representation of Graphs

Consider the graph of Figure 1.1 represented geometrically [3].

Figure 1.1: Geometric representation of a graph.

This graph of Figure 1.1 on 4 vertices is represented by the following 4 × 4 matrix M: (For a formal treatment on matrices, see Chapter 3.).

Here, 4 is the number of vertices of the graph. The (i, j) entry of the above matrix M is simply the number of arcs with its initial vertex at i and the terminal vertex at j. This matrix is called the adjacency matrix of the graph of figure.

More generally, for a n vertex graph G with vertex set X = {1, 2, …, n}, the adjacency matrix of G is the n × n matrix M = (m_ij) where

mij=number of arcs of the form(i,j).

Memory space for the adjacency matrix: Since an n × n matrix has exactly n² entries, the memory space necessary for the adjacency matrix representation of a graph is of order O(n²). The time complexity of initializing a graph by its adjacency graph is O(n²). This may preclude algorithms on graphs whose com...

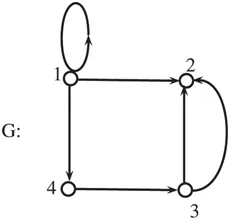
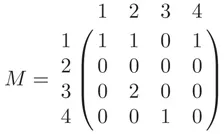
Table of contents

• Cover
• Half Title
• Title Page
• Copyright Page
• Dedication
• Contents
• List of Figures
• List of Tables
• Preface
• Acknowledgment
• Authors
• Chapter 1: Graph Algorithms I
• Chapter 2: Graph Algorithms II
• Chapter 3: Algebraic Structures I (Matrices, Groups, Rings, and Fields)
• Chapter 4: Algebraic Structures II (Vector Spaces and Finite Fields)
• Chapter 5: Introduction to Coding Theory
• Chapter 6: Cryptography
• Appendix A: Answers to Chapter 1—Graph Algorithms I
• Appendix B: Answers to Chapter 2—Graph Algorithms II
• Appendix C: Answers to Chapter 3—Algebraic Structures I
• Appendix D: Answers to Chapter 4—Algebraic Structures II
• Appendix E: Answers to Chapter 5—Introduction to Coding Theory
• Appendix F: Answers to Chapter 6—Cryptography
• Bibliography
• Index