Mathematical Economics

Arsen Melkumian

• Publisher: Routledge
• Year: 2012
• eBook ISBN: 9781136868986
• Edition: 1
• Topic: Business
• Subtopic: Business General
• Index: Business

This textbook, designed for a single semester course, begins with basic set theory, and moves briskly through fundamental, exponential, and logarithmic functions. Limits and derivatives finish the preparation for economic applications, which are introduced in chapters on univariate functions, matrix algebra, and the constrained and unconstrained optimization of univariate and multivariate functions. The text finishes with chapters on integrals, the mathematics of finance, complex numbers, and differential and difference equations.

Rich in targeted examples and explanations, Mathematical Economics offers the utility of a handbook and the thorough treatment of a text. While the typical economics text is written for two semester applications, this text is focused on the essentials. Instructors and students are given the concepts in conjunction with specific examples and their solutions.

1 Introduction

The purpose of this chapter is to familiarize the reader with basic concepts in set theory and introduce our notation. The first section introduces sets of natural, rational, irrational and real numbers and provides several examples of relations. The following section considers the polynomial functions frequently used by economists, linear, quadratic and cubic, and demonstrates how to minimize a quadratic profit function (or any quadratic function for that matter). The concepts introduced in this chapter will be used frequently, so a thorough understanding of the chapter’s material is essential to the remainder of this book.

1.1 Basic set theory

The numbers that we use for counting, namely 1, 2, 3, …, are called natural numbers. Number 1 is the lowest natural number and there are infinitely many natural numbers. A collection of natural numbers, such as 1, 7, 25 and 46, is referred to as a set.

In general, a set is a collection of objects. These objects may be natural numbers, coins, movies, people and so on. The objects in a set are referred to as the elements of the set. In some cases we can define a set by enumeration of the elements. For instance, natural numbers 2, 7, 11 and 23 can form a set

In this case, we have defined our set S by enumeration of the elements. The set S is finite, as it contains a finite number of elements. When a set is infinite or contains a lot of elements, we are forced to define it by description. For example, the set

reads as follows: “W is the set of all natural numbers x, such that x is greater than five.” The vertical bar in the description of W simply means “such that.” Set W is infinite, as there are infinitely many natural numbers greater than five.

If the elements of a set can be counted using natural numbers 1, 2, 3, 4 and so on, then the set is considered to be countable. In particular, set S as well as any other finite set is countable. Infinite sets may be countable or uncountable. For example, set W is countable since its elements can be counted using natural numbers: the first element of W is 6, the second element of W is 7 and so on. The set of natural numbers, referred to as ℕ and given by

is also countable.

Now, let us define the set of integers

Clearly, ℤ is an infinite set that is countable. The set of integers ℤ is also known as the set of whole numbers. We shall write ℤ⁺ or ℤ⁻ to refer to the set of positive or negative integers, respectively.

EXAMPLE 1.1 Show that the set of all integers ℤ is countable.

Solution: The set of integers can be counted as follows: the first element of ℤ is 0, the second element of ℤ is 1, the third element of ℤ is −1, the fourth element of ℤ is 2, the fifth element of ℤ is −2 and so on. The set is countable.

Now, consider another set:

This is called the set of rational numbers. Rational numbers are simply fractions in lowest terms. It could be shown that the set of rational numbers is countable. The set of rational nu...

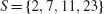
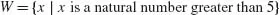
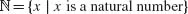
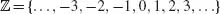
Table of contents

• Cover
• Halftitle
• Title
• Copyright
• Contents
• Preface
• Acknowledgements
• 1 Introduction
• 2 Fundamental functions and series
• 3 Exponential and logarithmic functions
• 4 Limits and derivatives
• 5 Optimization of univariate functions
• 6 Matrix algebra
• 7 Further topics in matrix algebra
• 8 Optimization of bivariate and multivariate functions
• 9 Indefinite and definite integrals
• 10 Mathematics of finance
• 11 Complex numbers
• 12 Difference and differential equations
• Answers to odd-numbered problems
• Index