Oscillations and Waves

An Introduction, Second Edition

Richard Fitzpatrick

• Publisher: CRC Press
• Year: 2018
• Print ISBN: 9781138480353
• eBook ISBN: 9781351063081
• Topic: Physical Sciences
• Subtopic: Condensed Matter

Emphasizing physics over mathematics, this popular, classroom-tested text helps advanced undergraduates acquire a sound physical understanding of wave phenomena. This second edition of Oscillations and Waves: An Introduction contains new widgets, animations in Python, and exercises, as well as updated chapter content throughout; continuing to ease the difficult transition for students between lower-division courses that mostly encompass algebraic equations and upper-division courses that rely on differential equations.

Assuming familiarity with the laws of physics and college-level mathematics, the author covers aspects of optics that crucially depend on the wave-like nature of light, such as wave optics. Examples explore discrete mechanical, optical, and quantum mechanical systems; continuous gases, fluids, and elastic solids; electronic circuits; and electromagnetic waves. The text also introduces the conventional complex representation of oscillations and waves during the discussion of quantum mechanical waves.

Features:

• Fully updated throughout and featuring new widgets, animations, and end of chapter exercises to enhance understanding
• Offers complete coverage of advanced topics in waves, such as electromagnetic wave propagation through the ionosphere
• Includes examples from mechanical systems, elastic solids, electronic circuits, optical systems, and other areas

CHAPTER 1

Simple Harmonic Oscillation

1.1 INTRODUCTION

The aim of this chapter is to investigate a particularly straightforward type of motion known as simple harmonic oscillation, and also to introduce the differential equation that governs such motion, which is known as the simple harmonic oscillator equation. We shall discover that simple harmonic oscillation always involves a back and forth flow of energy between two different energy types, with the total energy remaining constant in time. We shall also learn that the linear nature of the simple harmonic oscillator equation greatly facilitates its solution. In this chapter, examples are drawn from simple mechanical and electrical systems.

1.2 MASS ON SPRING

Consider a compact mass m that slides over a frictionless horizontal surface. Suppose that the mass is attached to one end of a light horizontal spring whose other end is anchored in an immovable wall. See Figure 1.1. At time t, let x(t) be the extension of the spring; that is, the difference between the spring’s actual length and its unstretched length. x(t) can also be used as a coordinate to determine the instantaneous horizontal displacement of the mass.

The equilibrium state of the system corresponds to the situation in which the mass is at rest, and the spring is unextended (i.e., x = ẋ = 0, where ̇. ≡ d/dt). In this state, zero horizontal force acts on the mass, and so there is no reason for it to start to move. However, if the system is perturbed from its equilibrium state (i.e., if the mass is displaced horizontally, such that the spring becomes extended) then the mass experiences a horizontal force given by Hooke’s law,

$$f\left(x\right)=-kx.$$ (1.1)

FIGURE 1.1 Mass on a spring.

Here, k > 0 is the so-called force constant of the spring. The negative sign in the preceding expression indicates that f(x) is a so-called restoring force that always acts to return the displacement, x, to its equilibrium value, x = 0 (i.e., if the displacement is positive then the force is negative, and vice versa). Note that the magnitude of the restoring force is directly proportional to the displacement of the mass from its equilibrium position (i.e., | f | ∝ x). Hooke’s law only holds for relatively small spring extensions. Hence, the mass’s displacement cannot be made too large, otherwise Equation (1.1) ceases to be valid. Incidentally, the motion of this particular dynamical ...

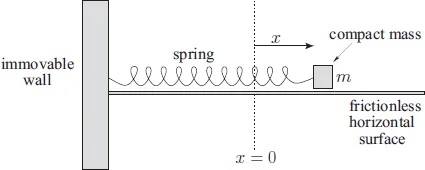
Table of contents

• Cover
• Half Title
• Title Page
• Copyright Page
• Table of Contents
• Preface
• Chapter 1 Simple Harmonic Oscillation
• Chapter 2 Damped and Driven Harmonic Oscillation
• Chapter 3 Coupled Oscillations
• Chapter 4 Transverse Standing Waves
• Chapter 5 Longitudinal Standing Waves
• Chapter 6 Traveling Waves
• Chapter 7 Multi-Dimensional Waves
• Chapter 8 Wave Pulses
• Chapter 9 Dispersive Waves
• Chapter 10 Wave Optics
• Chapter 11 Wave Mechanics
• Bibliography
• Index