Game Theory

A Modeling Approach

Richard Alan Gillman, David Housman

• Publisher: Chapman and Hall/CRC
• Year: 2019
• Print ISBN: 9781482248098
• eBook ISBN: 9781482248166
• Topic: Mathématiques
• Subtopic: Opérations

Game Theory: A Modeling Approach quickly moves readers through the fundamental ideas of the subject to enable them to engage in creative modeling projects based on game theoretic concepts.

The authors match conclusions to real-world scenarios and applications. The text engages students in active learning, group work, in-class discussions and interactive simulations.

Each chapter provides foundation pieces or adds more features to help readers build game theoretic models. The chapters include definitions, concepts and illustrative examples. The text will engage and challenge both undergraduate and graduate students.

Features:

• Enables readers to apply game theorty to real-world scenarios
• Chapters can be used for core course materials or independent stuides
• Exercises, included at the end of the chapters, follow the order of the sections in the text
• Select answers and solutions are found at the end of the book
• Solutions manual for instructors is available from the authors

Chapter 1

Models and Games

Mathematical modeling bridges the mental distance between the real world in which we operate and the abstract world that provides guiding structures. Game theory has a collection of mathematical concepts and tools useful in modeling scenarios having multiple interacting decision makers: people, businesses, governments, animals, and genes. We review the basic components of mathematical modeling, learn the definition of a game, and explore two scenarios amenable to game theoretic modeling, a particular type of mathematical modeling. In addition, we reflect on the general rationality assumptions underlying game theory.

1.1Introduction to Modeling

While the development of a mathematical theory is interesting in its own right, the primary value of game theory, and the principal focus of this volume, is its ability to model real-world scenarios. Mathematical modeling helps provide a scientific understanding of real-world phenomena, using the tools of mathematics to clarify issues and provide precise answers. It is worth mentioning that mathematical modeling is one of many ways to perceive the world: one that is surprisingly accurate for describing the physical world. However, in certain situations, the output of a mathematical model should be considered in light of social, cultural, and ethical values. For example, Schiemann [93] builds a mathematical model to assess whether interrogative torture is efficient. While the mathematical model has value, it isn’t designed to depict the ethical issues surrounding torture. Other types of models which represent torture pictorially or through fictional accounts, for example, may be more suited for assessing moral value.

In the natural sciences, modeling has descriptive, explanatory, and predictive goals: what is, why it is, and what will happen. In the social sciences and humanities, modeling can also have a normative goal: what ought to be. With these varied purposes of mathematical modeling in mind, we begin with an overview of the mathematical modeling process.

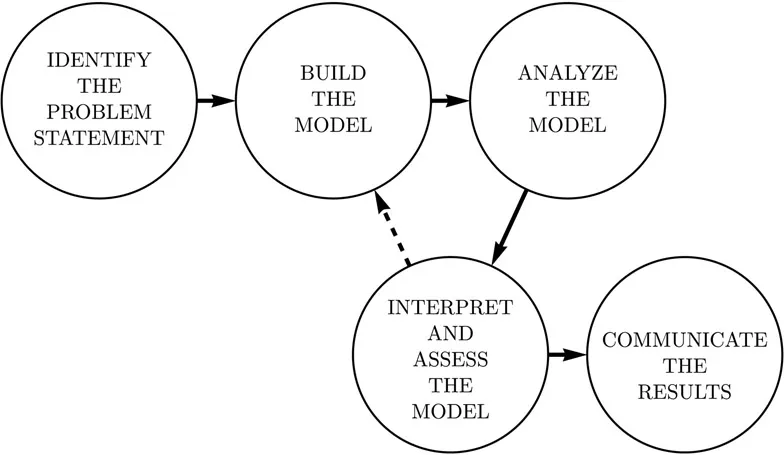
The first step in mathematical model building is to articulate a precise problem statement. Many, if not all, real-world scenarios are highly complex with many different components and peculiarities. By reviewing the appropriate literature, determining the data that is available, and reviewing the tools we have to work with, we can articulate a well-defined problem statement that we can reasonably hope to answer. This problem statement will enable us to determine what we want the output of our model to be by eliminating output that does not answer the question posed in the problem statement.

With the problem statement determined, the second step in the modeling process is to construct a mathematical structure (model) that represents the scenario and addresses the problem statement. To do this, we must identify the important factors to incorporate into our model and quantify those factors in the form of variables. We’ll necessarily make assumptions to simplify the model we are building; it is important to identify and document these assumptions. Because of the complexity of the scenario, or the limits on our ability to use particular tools, it may take several iterations of the modeling process to complete this step, as we continue to refine the model and uncover more data relevant to the problem that we have posed.

The third step in the modeling process is to analyze the model. That is, we use the appropriate mathematical tools to determine solutions to the mathematical problems posed by the model. It is important to realize that the relative sophistication of the tools we are using does not reflect directly on the quality of our modeling process. Very simple tools can sometimes be used to describe complex relationships and, unfortunately, sometimes straight-forward solutions are hidden in complex machinery. Much of the work of this volume will be devoted to helping us develop the tools necessary to find solutions to problems posed by game theoretical models.

The fourth step of the modeling process is to assess both the solutions and the model. How well do the solutions that we found correspond with the original scenario? Are they reasonable? Can they be validated by comparison to solutions that others have found in practice? How sensitive is our model to changes in the parameters that we established? How limiting were the assumptions that we made? What changes in the model might improve its accuracy?

Models may be assessed in terms of three traits: fidelity, cost, and flexibility. Fidelity assesses how well the model corresponds to the scenario being studied. Models that use real-world data typically have higher levels of fidelity than models which make significant assumptions about data. Secondly, we consider the cost to develop and implement the model. Considering real-world data again, we recognize that gathering that data has a much higher cost in time and money than models that use standardized formats. Finally, flexibility measures how sensitive the model is to variations in conditions. Again, models relying on real-world data are likely to be less flexible because of the effort required in gathering data while standardized models are more flexible with their various parameters being well-defined. The game-theoretic models described in this volume will typically have highly variable fidelity (because this depends significantly on the modeler’s willingness to gather basic data), low cost (because their structure and implementation are straightforward), and reasonable flexibility (because of their internal structures).

These four steps may need to be iterated several times to refine and extend the model. Once we have reached a satisfactory model that accurately represents the real-world phenomena we set out to model, the fifth and final step in the mathematical modeling process is to implement the model and report the results. While it is not strictly part of the modeling process, we should expect and plan to share our results with some audience. For whom were we undertaking this modeling exercise? What do they expect us to report back to them? Answers to these questions may also have a impact on the type, complexity, and the level of detail that we might want to include in our model.

Figure 1.1 displays this process graphically. Adapted from [40], it emphasizes the iterative nature of the modeling process, with attention to the fact that we may loop through the process in different patterns.

Figure 1.1Mathematical Modeling Process. Adapted from GAIMME: Guidelines for Assessment and Instruction in Mathematical Modeling Education, Sol Garfunkel and Michelle Montgomery, editors, Consortium for Mathematics and Its Applications and Society for Industrial and Applied Mathematics, Philadelphia, 2016. Used with permission.

1.2Introduction to Game Theory

People and organizations make decisions every day to take actions in complicated environments as they interact with others. Their goals are to influence the outcome of an interaction with others in ways that they perceive to be beneficial. Examples can include the following:

•Office coffee sharing In many offices, there is a shared coffee pot, and the employees voluntarily contribute to a pool of money to replenish the supplies. Each employee that wants to enjoy the coffee must decide how much, if anything, to contribute to the pool.

•Negotiations between countries that share a border Each of the countries is attempting to pick a course of action that will both ensure security as well as facilitate economic growth and the well-being of its citizens.

•Representatives voting Elected representatives may have to vote on policies that directly benefit themselves, like their own raises. Each may want the resolution to pass, but doesn’t want to appear self-interested.

•Sharing of water resources In many regions, governments need to negotiate how to share common water resources. In these negotiations, each government needs to balance the personal needs of its citizens, needs of the agricultural community, and environmental sustainability.

Game theory is the mathematical field that has been intentionally developed to advise people and organizations on what their optimal strategy is and what outcome they might expect from following this strategy in situations such as th...

Table of contents

• Cover
• Half Title
• Series Page
• Title Page
• Copyright Page
• Contents
• Preface
• Acknowledgments
• Chapter 1: Models and Games
• Chapter 2: Player Preferences
• Chapter 3: Simultaneous Play
• Chapter 4: Bilateral Agreements
• Chapter 5: Sequential Play
• Chapter 6: Missing Information
• Chapter 7: Repetitious Play
• Chapter 8: Multilateral Agreements
• Chapter 9: Resource Allocation
• Appendix A: Selected Answers
• Bibliography
• Index