Explaining and Exploring Mathematics

Teaching 11- to 18-year-olds for understanding and enjoyment

Christian Puritz

• Publisher: Routledge
• Year: 2017
• Print ISBN: 9781138680197
• eBook ISBN: 9781317191308
• Edition: 1
• Topic: Education
• Subtopic: Education General

Explaining and Exploring Mathematics is designed to help you teach key mathematical concepts in a fun and engaging way by developing the confidence that is vital for teachers. This practical guide focuses on improving students' mathematical understanding, rather than just training them for exams. Covering many aspects of the secondary mathematics curriculum for ages 11-18, it explains how to build on students' current knowledge to help them make sense of new concepts and avoid common misconceptions.

Focusing on two main principles to improve students' understanding: spotting patterns and extending them to something new, and relating the topic being taught to something that the pupils already understand, this book helps you to explore mathematics with your class and establish a successful teacher-student relationship.

Structured into a series of lessons, Explaining and Exploring Mathematics is packed full of practical advice and examples of the best way to answer frequently asked questions such as:

• Do two minuses really make a plus?
• Why doesn't 3a + 4b equal 7ab?
• How do you get the area of a circle?
• Why do the angles of a triangle add up to 180°?
• How can you integrate 1/x and calculate the value of e?

This book will be essential reading for all trainee and practising teachers who want to make mathematics relevant and engaging for their students.

p.3

Part I

11–14 years old

p.5

1	Decimals and multiplication by 10, etc.

Teacher:	“Look at this number, 3528. What is the 3 actually worth?”
Mike:	“Three thousand; and the 5 is 500.”
Nadeem:	“The 2 is 20, two 10s, and the 8 is units, just 8.”
Teacher:	“Good. What happens as you move from left to right in a number like 3528?”
Linda:	“Each time you move right the value is less, ten times smaller.”
Teacher:	“Right; so what about 3528.79? The dot after the 8 is the decimal point, which comes after the units.”
Nadeem:	“So the 7 has to be ten times smaller than if it were in the units.”
Linda:	“That makes it 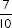, doesn’t it?”

If a pupil can’t see that yet, it can help to draw a rectangular chocolate bar with lines to divide it into ten equal pieces, shade one piece and ask “What would you call this?”, hopefully leading to the fact the shaded piece is one tenth. At the next stage one of the unshaded tenths can be divided into ten smaller parts, followed by the question “How many of these smaller parts would make a whole bar? So what do you call each smaller part?”

Mike:	“Yes, and then the 9 is ten times smaller again, so it’s .”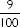
Teacher:	“Good, you’re getting the idea. The pattern of each step to the right giving a value ten times smaller continues on into the fractional part of the number. The way we write numbers using just ten digits and making the value of each depend on its position was invented centuries ago in India, copied by the Arabs and brought by them to Europe, where previously the Roman numerals were used; they are still used sometimes for dates, but the place value system is much better for doing sums. What is 528 × 10?”
Linda:	“That easy, 5280.”

p.6

Teacher:	“Yes; now why does putting a 0 on the end make the number ten times bigger?”
Mike:	“It’s because the 0 now occupies the units place, making the other digits move one place to the left, thus becoming ten times bigger.”
Teacher:	“That’s right. The introduction of a symbol for zero was an important step. The Babylonians had a place value system based on 60 (which is why we still have 60 minutes – minute parts – in an hour and 60 seconds – second minute parts – in a minute; but they didn’t have a proper symbol for 0, so for instance the numbers 3 and 3 × 60 = 180 looked the same, just as in our system 3 could be three or thirty or three hundred if we didn’t have 0.”
Nadeem:	“So what about 528.79 × 10?”
Teacher:	“OK, the 5, 2 and 8 each move one place to the left to make them 10 times bigger, but then so do the 7 and the 9.”
Mike:	“So it’s 5287.9?”
Teacher:	“Yes; the 7 was worth 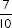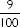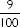and is now 7 units or just 7, while the 9 was and changes to . Every digit moves one place to the left.”
Linda:	“Or can you just move the decimal one place to the right; that has the same effect, doesn’t it?”
Teacher:	“Yes indeed. Now what about 528.79 × 100?”
Mike:	“You move the d...

Table of contents

• Cover Page
• Explaining and Exploring Mathematics
• Title
• Copyright
• Contents
• Introduction
• Part I 11–14 Years Old
• Part II 14–16 Years Old
• Part III 16–18 years Old143
• Index