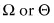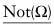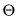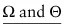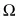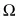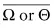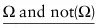Paradoxes

Roy T. Cook

• Publisher: Polity
• Year: 2013
• ISBN:
  9780745665511
• Edition: 1
• Topic: Philosophie
• Subtopic: Logique en philosophie

Paradoxes are arguments that lead from apparently true premises, via apparently uncontroversial reasoning, to a false or even contradictory conclusion. Paradoxes threaten our basic understanding of central concepts such as space, time, motion, infinity, truth, knowledge, and belief. In this volume Roy T Cook provides a sophisticated, yet accessible and entertaining, introduction to the study of paradoxes, one that includes a detailed examination of a wide variety of paradoxes. The book is organized around four important types of paradox: the semantic paradoxes involving truth, the set-theoretic paradoxes involving arbitrary collections of objects, the Soritical paradoxes involving vague concepts, and the epistemic paradoxes involving knowledge and belief. In each of these cases, Cook frames the discussion in terms of four different approaches one might take towards solving such paradoxes. Each chapter concludes with a number of exercises that illustrate the philosophical arguments and logical concepts involved in the paradoxes. Paradoxes is the ideal introduction to the topic and will be a valuable resource for scholars and students in a wide variety of disciplines who wish to understand the important role that paradoxes have played, and continue to play, in contemporary philosophy.

1

The Care and Feeding of your New Paradoxes

In an episode of Matt Groening’s The Simpsons, Homer Simpson asks Ned Flanders the following question:

“Could Jesus microwave a burrito so hot that even he couldn’t eat it?”

The puzzle, of course, if this: If we answer “no,” then we have admitted that there is a task – microwaving a burrito so hot that it cannot be eaten – that Jesus could not even in principle perform, violating his supposed omnipotence. If we answer “yes,” however, then we have again admitted that there is a task that Jesus cannot perform – namely, eating said burrito. Either way, we seem to be violating Jesus’ omnipotence, and thus if Jesus really is omnipotent, then we seem stuck with a contradiction. This is a paradox (one known as the paradox of omnipotence, and more commonly formulated in terms of God creating a rock too heavy to lift).

A paradox (or aporia) is a type of argument. In particular, a paradox is an argument that:

(a) Begins with premises that seem uncontroversially true.

(b) Proceeds via reasoning that seems uncontroversially valid.

(c) Arrives at a conclusion that is a contradiction, is false, or is otherwise absurd, inappropriate, or unacceptable.

Conditions (a) and (b) are for the most part straightforward. Condition (c), however, deserves more comment.

(c) asserts that the problematic conclusion involved in a paradox must be a contradiction, false, or otherwise absurd or inappropriate. A contradiction is a statement that is not only false, but that must be false, where this guarantee holds in virtue of the logical, or grammatical, form of the statement. For example, any claim of the form:

Φ and not(Φ)

is a contradiction, since no statement can be both true and false (where Φ is a statement, “not(Φ)” abbreviates the grammatically more careful, but inconveniently unwieldy, statement “it is not the case that Φ”). Contradictions come in other flavors, however. In particular, I will in what follows sometimes make use of the underappreciated fact that (again, at least in standard classical treatments of logic) any statement of the form:

Φ if and only if not(Φ)

is also a contradiction.

Paradoxes need not result in outright contradictions, however. An argument will still be a paradox if the conclusion is false, but not a contradiction. For example, in Chapter 6 we will examine an argument (the Fitch Paradox) that purports to show that if all truths are knowable, then all truths are known. The claim that all truths are known is not a contradiction, since it does not describe a situation that is impossible (or, at least, doesn’t seem to at first glance – see the discussion of blindspots in Chapter 6). The claim that all true statements are known is clearly false, however, which is enough to demonstrate that something must have gone wrong with the argument, and that the argument is therefore a paradox.

On the definition given above, paradoxes can also involve a conclusion that is neither a contradiction nor even a falsehood. There are paradoxes that consist of arguments based on apparently true premises that lead to conclusions that might be true, but which, in some very real sense, should not follow from the premises in question. For example, in Chapter 3 we will examine a paradox (the Curry Paradox) whose premises do nothing more than state conditions that truth ought to satisfy, and whose reasoning involves nothing more than basic inferences involving the expression “if … then. … ” Versions of this paradox can be constructed where the conclusion is, in fact, a true statement such as “Snow is white,” or where the conclusion is a statement that could have been true such as “Santa Claus exists.” The argument in this case is a paradox, not because “Snow is white” is a contradiction or a falsehood, but because we should not be able to demonstrate that snow is white based merely on considerations – that is, on premises – regarding philosophical concepts such as truth and on logical operations such as “if … then. … ”

Thus, paradoxes do not require conclusions that are contradictory, or even false. It is worth noting that there is something particularly disturbing about paradoxes whose conclusions take the form of a contradiction, however. In cases where the conclusion appears to be merely false, absurd or unacceptable, but not a contradiction, one strategy for dealing with the paradox is to decide that we were mistaken, and that the conclusion was not false, absurd, or unacceptable after all. Similarly, if the conclusion of a paradox is merely inappropriate (such as in the Curry Paradox “Snow is white” case above), one strategy is to re-evaluate what type of conclusions one should expect to follow from various sorts of premises (e.g. we might decide that questions about the color of objects really should follow from premises regarding truth and logic). The point is not that this sort of solution will always, or even often, be successful. On the contrary, in many if not most cases this sort of response is immensely implausible. The point, rather, is that in the case of paradoxes that involve a contradiction, this sort of response is unavailable as a matter of principle.

The problem with contradiction-involving paradoxes is deeper than the mere implausibility of accepting a contradiction as true. As we shall see, there are responses to paradoxes that make exactly this move. The problem is that this sort of response requires a solution to a further problem: the fact that a contradiction entails anything – at least, it does so in most accounts of logic and logical consequence. A theory that entails that every statement is true is called a trivial theory.

The argument that any theory that contains a contradiction is a trivial theory is simple. Assume that we have a contradiction of the form:

Φ and not Φ

We can now argue as follows: Given the truth of the offset statement above, it follows that Φ is true. So, for any statement ψ whatsoever:

Φ or Ψ

is true. Since:

Not(Φ)

is also true, we can combine the previous two lines, via the rule of inference known as disjunctive syllogism:

to conclude that ψ is true. A similar proof can be given if the contradiction is of the form:

Φ if and only if not(Φ)

As a result, anyone who accepts all of the inference rules used in the proof above – that is, and-elimination (or adjunction):

or-introduction (or addition):

and disjunctive syllogism – will also have to accept as valid the inference rule known as explosion or ex falso quodlibet:

In short, in classical logic (and in many non-classical accounts of logic) anything follows from a contradiction.

Thus, anyone who wishes to accept the conclusion of a paradox involving a contradiction will need to reject one or more of the rules used above. Logics that reject the validity of ex falso quodlibet are known as paraconsistent logics, while logics that not only reject this classical rule but allow for the possibility that some contradictions are true are known as dialethic logics. As we shall see in Chapter 2, this latter sort of response to paradoxes – dialetheism – usually proceeds by denying disjunctive syllogism.

Before moving on, it is worth noting that other definitions of the notion of paradox have been offered. For example, Roy Sorensen defines paradoxes rather loosely as follows:

I take paradoxes to be riddles. The oldest philosophical questions evolved from folklore and show vestiges of the verbal games that generated them. (2005: 3)

Sorensen understands a riddle to be a kind of question – one that typically has too many apparent answers. He fleshes this out a bit later in the same book:

The riddle theory of paradox allows for the possibility of meaningless paradoxes. Riddles need only appear to be genuine questions; they can instead be meaningless utterances that look like questions. Pseudoquestions need only appear to have good answers and so need only appear to have an overabundance of good answers. (2005: 36)

Note that this passage implies that some paradoxes, on Sorensen’s understanding of the notion, do not have genuine solutions. Given the focus on solutions to paradoxes adopted here, this already provides some motivation for formulating a somewhat narrower conception of paradox.

Anything that is a paradox on the definition we have adopted here will also be a paradox on Sorensen’s account (since apparently acceptable arguments leading to unacceptable conclusions surely present some sort of “riddle” or “puzzle”), but not vice versa. On the contrary, it seems likely that most if not all puzzles and problems within philosophy (as well as many puzzles and problems in other disciplines) will fall under Sorensen’s understanding of paradox. For our purposes, we will keep to the narrower reading – one that understands a paradox as a kind of argument that concludes with a contradiction, falsehood, absurdity, or other unacceptable statement. This is not to say that Sorensen is wrong – after all, it is probably pointless and silly to argue too seriously about the ‘right’ usage of such an esoteric term as “paradox.” Nevertheless, the narrower understanding adopted here will help us to keep our investigations tightly focused.

A related notion that is also worth examining is the slightly more rarified notion of an antinomy. Simply put, an antinomy is a pair of arguments where:

(a) Each argument begins with premises that seem uncontroversially true.

(b) Each argument proceeds via reasoning that seems uncontroversially valid.

(c) The conclusions of the arguments are incompatible with each other.

As was the case with paradoxes, we can distinguish between a number of senses in which the two conclusions in question might be incompatible with each other: Their conjunction might be a contradiction, or might merely be false, or might be absurd or unacceptable in some other sense.

For our purposes, we need not treat antinomies as a category separate from paradoxes. The reason is simp...