A Primer of Signal Detection Theory

Don McNicol

• Publisher: Psychology Press
• Year: 2005
• Print ISBN: 9781138149205
• eBook ISBN: 9781135604677
• Topic: Psychology
• Subtopic: Developmental Psychology
• Index: Psychology

A Primer of Signal Detection Theory is being reprinted to fill the gap in literature on Signal Detection Theory--a theory that is still important in psychology, hearing, vision, audiology, and related subjects. This book is intended to present the methods of Signal Detection Theory to a person with a basic mathematical background. It assumes knowledge only of elementary algebra and elementary statistics. Symbols and terminology are kept at a basic level so that the eventual and hoped for transfer to a more advanced text will be accomplished as easily as possible.

Intended for undergraduate students at an introductory level, the book is divided into two sections. The first part introduces the basic ideas of detection theory and its fundamental measures. Its aim is to enable the reader to be able to understand and compute these measures. It concludes with a detailed analysis of a typical experiment and a discussion of some of the problems which can arise for the potential user of detection theory. The second section considers three more advanced topics: threshold theory, the extension of detection theory, and an examination of Thurstonian scaling procedures.

Chapter 1
WHAT ARE STATISTICAL DECISIONS?

AN EXAMPLE

Often we must make decisions on the basis of evidence which is less than perfect. For instance, a group of people has heights ranging from 5 ft 3 in. to 5 ft 9 in. These heights are measured with the group members standing in bare feet. When each person wears shoes his height is increased by 1 inch, so that the range of heights for the group becomes 5 ft 4 in. to 5 ft 10 in. The distributions of heights for members of the group with shoes on and with shoes off are illustrated in the histograms of Figure 1.1.

FIGURE 1.1

You can see that the two histograms are identical, with the exception that s, the ‘Shoes on’ histogram, is 1 in. further up the X-axis than n, the ‘Shoes off histogram.

Given these two distributions you are told that a particular person is 5 ft 7 in. tall and from this evidence you must deduce whether the measurement was taken with shoes on or with shoes off. A look at these histograms in Figure 1.1 shows that you will not be able to make a decision which is certain to be correct. The histograms reveal that 3/16ths of the group is 5 ft 7 in. tall with shoes off and that 4/16ths of the group is 5 ft 7 in. tall with shoes on. The best bet would be to say that the subject had his shoes on when the measurement was taken. Furthermore, we can calculate the odds that this decision is correct. They will be (4/16)/(3/16), that is, 4/3 in favour of the subject having his shoes on.

You can see that with the evidence you have been given it is not possible to make a completely confident decision one way or the other. The best decision possible is a statistical one based on the odds favouring the two possibilities, and that decision will only guarantee you being correct four out of every seven choices, on the average.

It is possible to calculate the odds that each of the eight heights

TABLE 1.1 The odds favouring the hypothesis ‘Shoes on’ for the eight possible heights of group members.

of the group was obtained with shoes on. This is done in Table 1.1. The probabilities in columns 2 and 3 have been obtained from Figure 1.1.

For the sake of brevity we will refer to the two states of affairs ‘Shoes on’ and ‘Shoes off as states s and n respectively.

It can be seen that the odds favouring hypothesis s are calculated in the following way:

For a particular height, which we will call x, we take the probability that it will occur with shoes on and divide it by the probability that it will occur with shoes off. We could, had we wished, have calculated the odds favouring hypothesis n rather than those favouring s, as has been done in Table 1.1. To do this we would have divided column 2 entries by column 3 entries and the values in column 4 would then have been the reciprocals of those which appear in the table.

Looking at the entries in column 4 you will see that as the value of x increases the odds that hypothesis s is correct become more favourable. For heights of 67 in. and above it is more likely that hypothesis s is correct. Below x=67 in. hypothesis n is more likely to be correct. If you look at Figure 1.1 you will see that from 67 in. up, the histogram for ‘Shoes on’ lies above the histogram for ‘Shoes off. Below 67 in. the ‘Shoes off histogram is higher.

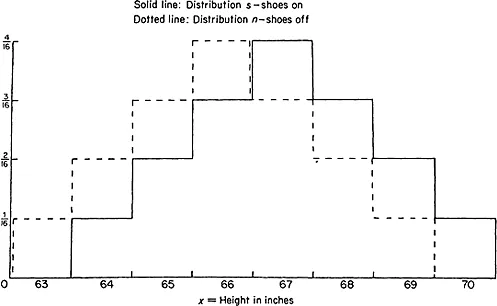
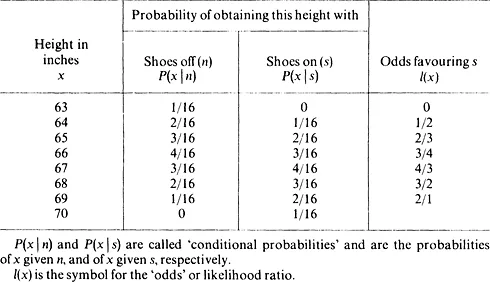SOME DEFINITIONS

With the above example in mind we will now introduce some of the terms and symbols used in signal detection theory.

The evidence variable

In the example there were two relevant things that could happen. These were state s (the subject had his shoes on) and state n (the subject had his shoes off). To decide which of these had occurred, the observer was given some evidence in the form of the height, x, of the subject. The task of the observer was to decide whether the evidence favoured hypothesis s or hypothesis n.

As you can see we denote evidence by the symbol x.¹ Thus x is called the evidence variable. In the example the values of x ranged from x=63 in. to x=70 in. In a psychological experiment x can be identified with the sensory effect produced by a stimulus which may be, for example, a range of illumination levels, sound intensities, or verbal material of different kinds.

Conditional probabilities

In the example, given a particular value of the evidence variable, say x=66 in., Table 1.1 can be used to calculate two probabilities:

(a) P(x|s): that is, the probability that the evidence variable will take the value x given that state s has occurred. In terms of the example, P(x|s) is the probability that a subject is 66 in. tall given that he is wearing shoes. From Table 1.1 it can be seen that for x=66 in.,

(b) P(x|n): the probability that the evidence variable will take the value x given that state n has occurred. Table 1.1 shows that for x=66 in.,

P(x|s) and P(x|n) are called conditional probabilities because they represent the probability of one event occurring conditional on another event having occurred. In this case we have been looking at the probability of a person being 66 in. tall given that he is (or conditional on him) wearing shoes.

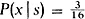
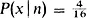
The likelihoo...

Table of contents

• Foreword
• Preface
• Contents
• Chapter 1 WHAT ARE STATISTICAL DECISIONS?
• Chapter 2 NON-PARAMETRIC MEASURES OF SENSITIVITY
• Chapter 3 GAUSSIAN DISTRIBUTIONS OF SIGNAL AND NOISE WITH EQUAL VARIANCES
• Chapter 4 GAUSSIAN DISTRIBUTIONS OF SIGNAL AND NOISE WITH UNEQUAL VARIANCES
• Chapter 5 CONDUCTING A RATING SCALE EXPERIMENT
• Chapter 6 CHOICE THEORY APPROXIMATIONS TO SIGNAL DETECTION THEORY
• Chapter 7 THRESHOLD THEORY
• Chapter 8 THE LAWS OF CATEGORICAL AND COMPARATIVE JUDGEMENT
• BIBLIOGRAPHY
• Appendix 1 ANSWERS TO PROBLEMS
• Appendix 2 LOGARITHMS
• Appendix 3 INTEGRATION OF THE EXPRESSION FOR THE LOGISTIC CURVE
• Appendix 4 TABLES
• INDEX