Mathematical and Analogical Reasoning of Young Learners

Lyn D. English

• Publisher: Routledge
• Year: 2004
• eBook ISBN: 9781135638696
• Topic: Education
• Subtopic: Education General

Mathematical and Analogical Reasoning of Young Learners provides foundational knowledge of the nature, development, and assessment of mathematical and analogical reasoning in young children. Reasoning is fundamental to understanding mathematics and is identified as one of the 10 key standards for school mathematics for the new millennium. The book draws on longitudinal and cross-cultural studies, conducted in the United States and Australia, of children's reasoning development as they progressed from preschool through the end of second grade.

The multifaceted analysis of young children's development of mathematical and analogical reasoning focuses on individual learners, their learning environments, and the interaction between the two. The multidisciplinary team of authors present multiple perspectives and multiple methodologies, and provide valuable information on organizing and sustaining interdisciplinary and cross-cultural inquiry. Key issues addressed include:
*the relationship between mathematical and analogical reasoning;
*how changes in children's reasoning relate to the implicit instruction they receive in their classrooms;
*analyses of the participating teachers' knowledge, beliefs, and practices with respect to mathematical and analogical reasoning of young learners; and
*ways in which we might promote development of mathematical and analogical reasoning in young children.

This volume is highly relevant for mathematics educators, researchers in mathematics education, educational psychologists, early childhood teachers, and others interested in mathematical development of young children, in particular, the development of their reasoning processes.

1

MATHEMATICAL AND ANALOGICAL REASONING IN EARLY CHILDHOOD

Lyn D. English

Queensland University of Technology

Those who observe young children at play will notice how readily they engage in mathematical activity. Young children spontaneously pose and solve problems that involve a broad range of mathematical ideas and processes. They enthusiastically embrace problems involving pattern, shape, number, and measurement as they explore their physical and social environments. Of particular significance in young children’s mathematical development are the reasoning processes they use in learning about their world, such as spatial and quantitative reasoning, deduction and induction, and analogical reasoning. Other processes such as classifying, comparing, representing, experimenting, and creating, also play a significant role in children’s mathematical development. As we illustrate in this book, children’s reasoning processes are powerful facilitators of their early learning, even more so than specific items of mathematical knowledge (Perry & Dockett, 2002).

Existing research, however, has yet to capture the range and extent of young children’s reasoning processes and the ways in which they use these in their informal and formal learning. One reason for this is that past research has mainly relied on children’s performance on specific reasoning tasks that were created by researchers and administered under test-like conditions. Typically, such studies focused on “the three c’s,” namely, “conservation (and related Piagetian and neo-Piagetian investigations), counting, and calculations” (Ginsburg, Pappas, & Seo, 2001, p. 8). These studies do not reveal the types of mathematical activities that children themselves instigate, nor the various ways in which children reason and learn during their free play. Naturalistic studies, on the other hand, can provide important insights into these issues. The studies of Ginsburg, Balfanz, and Greenes (2000), for example, have shown that children engage in mathematical activity for nearly half of their free playtime and, in doing so, display sophisticated thinking and reasoning processes.

The chapters of this book provide further evidence of young children’s reasoning abilities. We draw on rich sets of data from a longitudinal and cross-cultural study of young children’s reasoning development as they progressed from preschool through to the end of second grade. The participants included the children and their teachers from schools in Australia and the United States. We pay special attention to the children’s development of mathematical and analogical reasoning in their informative years, given that our earlier studies had highlighted the importance of analogical reasoning in children’s mathematical development (Alexander, White, & Daugherty, 1997). The purpose of this first chapter is to provide background information on analogical and mathematical reasoning, and to highlight the issues that are the focus of this book. Consideration is given first to the nature, role, and development of analogical reasoning.

ANALOGIES AND ANALOGICAL REASONING

Analogy provides an important example of what appears to be a highly general cognitive mechanism that takes specific inputs from essentially any domain that can be represented in explicit propositional form, and operates on them to produce inferences specific to the target domain. (Holyoak & Hummel, 2001, p. 162)

The powerful role of analogies in communicating, exploring, or transferring ideas has been well recognized since early times. Around the second century B.C., the Greek Stoic Chrysippus first used water waves to suggest the nature of sound, whereas in 1630, Galileo used the known orbit of the moon as the basis for his theory that the earth moves. Analogies are equally important in today’s society. We use analogies in many walks of life, such as decision making in law, business, and politics; scientific reasoning in the laboratory; and problem solving in daily living (Dunbar, 2001; English, 1999; Holyoak & Thagard, 1995).

Defined in a general sense, analogy is the ability to reason with relational patterns. Being able to detect patterns, to identify recurrences of the patterns in the face of variations in their elements, to abstract from the patterns, and to communicate these abstractions is a basic human achievement (Gentner, Holyoak, & Kokinov, 2001). In essence, analogy lies at the core of human cognition and appears to be closely linked to the development of general representational ability (Gentner & Rattermann, 1991; Hofstadter, 2001). Even children as young as 1 and 2 years of age display an ability to reason analogically (Goswami, 2001), where they use their understanding of familiar situations to help them construct new knowledge. For example, Hatano and Inagaki’s (1997) work on naïve biology has shown how young children use their knowledge about humans as the source for reasoning about less familiar animate objects. In one of our preschool classrooms, which we address in later chapters, we observed 5-year-old Elliott and James applying their knowledge of the human anatomy to interpret how trees function:

James:	The tree’s so fat. It’s got lots of blood in it.
Elliott:	Because inside the wood there’s some very liquid black stuff and I know that’s blood.
James:	No, water! The water goes in the tree and it could easily….. The water goes under, in the roots, and it goes up in the tree and gets blood.
Teacher:	Why do you think the trees need to have blood?
James:	Cos if they didn’t have blood they would die.
Teacher:	What does the blood do, do you think?
James:	Helps them stay alive.

As a fundamental process of human cognition, analogical reasoning has received considerable attention in the past 10–15 years. A good deal of the research, however, has focused on the reasoning of the adult population. It is only in recent years that studies have addressed young children’s ability to reason by analogy, reflecting a long-held view that such reasoning is a late developing skill (e.g., Inhelder & Piaget, 1958). Many of these studies have addressed classical four-term analogy problems of the type, mother is to daughter as father is to ? (e.g., the work of Inhelder & Piaget, 1958; Sternberg, 1977). Other studies have employed specifically designed problem analogies based on simple causal relations (e.g., rolling, pulling, stretching) involving real objects and models (e.g., Freeman, 1996; Goswami, 2001; Holyoak, Junn, & Billman, 1984). For example, Freeman’s base problem entailed a loose rubber band stretched between two poles to make a “bridge” for rolling an orange across, whereas the transfer problems included giving a doll a “ride” by stretching ribbon between two towers of different heights.

In contrast to the above types of study, children’s reasoning with analogies in everyday life and in specific disciplines, such as mathematics, has received considerably less attention. This is of particular concern, given that young children reason with pedagogical analogies from their earliest school experiences (English & Halford, 1995; Warfield & Yttri, 1999).

In the following sections, I present an overview of some of the diverse perspectives on analogical reasoning, on how it develops, and on the nature of young children’s capabilities in this domain. These perspectives are further examined in other chapters of this book.

Reasoning with Classical Analogies

Classical or conventional analogies take the form, A:B::C:D (e.g., tree:limb:: body:arm), where the C and D terms must be related in the same way as the A and B terms are linked. These analogies are basically proportional or relational problems and have been popular in IQ tests for many years. Structural theories, such as that of Piaget (e.g., Piaget, 1952; Inhelder & Piaget, 1958), have probably been the most frequently applied to analyses of reasoning with classical analogies. Such theories focus on the nature or sophistication of the relations that are drawn between the terms in a given analogy problem. These linkages between the A and B terms and between the C and D terms are defined as “lower order” relations. For example, in the analogy, tree:limb:: body:arm, it might be inferred that limb is a part of a tree and that arm is an appendage of the human body. These two associations between tree and limb and between body and arm are instances of lower order relations.

In contrast, higher order relations are those generated between more distant or removed concepts. These relations require the reasoner to determine some form of relational similarity between the more distant concepts. Thus, the ability to link the A:B pairing to the C:D pairing involves a higher order relation. For example, before the analogy, tree:limb::body:arm, can be solved, the reasoner must be able to determine what similarities are shared by trees and human bodies before she can generate a relation that would link tree:limb with body:arm. The reasoner might say that trees and bodies are both living and free-standing structures with outgrowths that serve some physiological or biological function. Such a superordinate relationship is an example of a higher order relation. The ability to identify these higher order relations is considered the “hallmark” of reasoning in solving these analogy types (Goswami, 1992).

Reasoning with classical analogies has also been analyzed in terms of the component processes involved, with Sternberg’s (e.g., 1977, 1981) componential theory of information processing being widely used. Here, the ability to reason analogically is viewed in terms of a number of component or elemental cognitive and metacognitive processes that are applied. This approach provides a much broader perspective on analogical reasoning capability than do structural theories. In brief, these components involve first, identifying each term of the analogy by encoding the attributes or characteristics of each term. Encoding is required for every term of the analogy problem. Next, is the process of inferring, where the relationship between the terms within each pairing is determined. Although inferring might appear to correspond to the structuralist conceptualization of a lower order relation, information-processing theorists see the possibility of multiple relations within the pairs being inferred during initial processing. The component process of mapping involves the linking of the A:B pairing to the C:D pairing by building a bridging inference on their relational similarity (cf., identifying a higher order relation). Finally, the process of applying involves generating or selecting a suitable term to complete the analogy, that is, to give it the required “conceptual balance” (i.e., establishing equivalence between the first and second pairing; Alexander et al., 1997, p. 121).

Reasoning with Problem Analogies

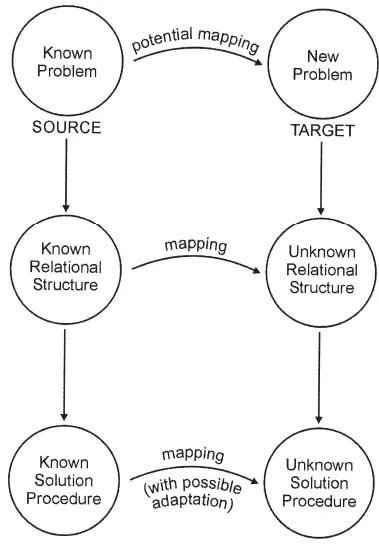
Studies addressing the ability to reason by analogy in problem-solving tasks have increased in popularity in the past couple of decades (e.g., Clement, 1993; Holyoak & Koh, 1985; Novick, 1995; Reed, 1987; Robins & Mayer, 1993; Stavy & Tirosh, 1993). In these studies, the reasoner must recognize the similarity in relational structure between a known problem (termed the base or source) and a new problem (the target); that is, a “structural alignment” or “mapping” between the two problems must be found (Bassok, 2001; Holyoak, Gentner, & Kokinov, 2001; refer Fig. 1.1). Story problems that comprise causal relations in general domains, such as the frequently cited “Genie” problem (Holyoak et al., 1984), have been popular. Here, the base problem involves a magic genie that rolled his carpet into a tube to provide a pathway for some valuable jewels. The target problem entails transporting some small rubber balls from one location to another. For children to solve the problem, they must recognize the intended relational correspondence between the carpet and the paper. In other words, with this type of protagonist story problem, the need to apply analogical reasoning is implicit, whereas in classical analogies it is explicit in the task structure. As discussed later, this implied need to reason analogically is not readily apparent to children and is one of the performance factors that must be taken into account in analyzing the development of analogical reasoning.

Word problems involving specific educational content, such as mathematical concepts, have been less popular in studies of children’s analogical reasoning than general story problems (English, 1997, 1998). This is in spite of the fact that solving such problems can contribute significantly to children’s conceptual development during mathematical problem solving and can also provide us with insights into children’s understanding of core content (English, 1997; Holyoak & Thagard, 1995; Silver, 1990). In one such study, for example, (English, 1997) 75 sixth graders (11-year-olds) were presented with sets of source (or base) problems involving comparison multiplication and division, combinatorial reasoning, and partitive division (sharing) with variable remainder use.

FIG. 1.1. Reasoning by analogy in problem-solving tasks.

The source problems were designed so that problems with the same mathematical structure had different cover stories and those with different structures had the same cover stories (this is similar to the cross-mapping condition used in other studies, such as Pierce & Gholson, 1994; Quilici & Mayer, 1996). For example, one of the comparison multiplication problems took the form, Sarah has 52 books on her shelf. Sue has 4 times as many as Sarah. How many books has Sue? A comparison division problem had the same cover story, namely, Mary has 72 books on her shelf. This is 3 times as many as Peter has. How many books has Peter? This problem design provided insight into children’s abilities to look beyond the surface features of the problems to detect the underlying structural features.

After sorting, classifying, and solving the source problem...

Table of contents

• Cover
• Half Title
• Title Page
• Copyright Page
• Dedication
• Table of Contents
• Preface
• 1 Mathematical and Analogical Reasoning in Early Childhood
• 2 Seeing the Possibilities: Constructing and Validating Measures of Mathematical and Analogical Reasoning for Young Children
• 3 Longitudinal and Cross-Cultural Trends in Young Children’s Analogical and Mathematical Reasoning Abilities
• 4 Classroom Discourse and the Development of Mathematical and Analogical Reasoning
• 5 Portraying Mathematical and Analogical Reasoning in the Young: Three Case Studies
• 6 Teachers’ Knowledge, Beliefs, and Practices and Mathematical and Analogical Reasoning
• 7 Case Studies of Teacher Beliefs, Knowledge, and Practices
• 8 Commentary: Analogical Reasoning and Mathematical Development
• 9 Commentary: Toward a Cognitive–Sociocultural Psychology of Mathematical and Analogical Development
• 10 Promoting the Development of Young Children’s Mathematical and Analogical Reasoning
• Author Index
• Subject Index