Game Theory and Exercises

Gisèle Umbhauer

• Publisher: Taylor & Francis
• Year: 2016
• Print ISBN: 9780415604222
• eBook ISBN: 9781317362982
• Edition: 1
• Topic: Business
• Subtopic: Business General
• Index: Business

Game Theory and Exercises introduces the main concepts of game theory, along with interactive exercises to aid readers' learning and understanding. Game theory is used to help players understand decision-making, risk-taking and strategy and the impact that the choices they make have on other players; and how the choices of those players, in turn, influence their own behaviour. So, it is not surprising that game theory is used in politics, economics, law and management.

This book covers classic topics of game theory including dominance, Nash equilibrium, backward induction, repeated games, perturbed strategie s, beliefs, perfect equilibrium, Perfect Bayesian equilibrium and replicator dynamics. It also covers recent topics in game theory such as level-k reasoning, best reply matching, regret minimization and quantal responses. This textbook provides many economic applications, namely on auctions and negotiations. It studies original games that are not usually found in other textbooks, including Nim games and traveller's dilemma. The many exercises and the inserts for students throughout the chapters aid the reader's understanding of the concepts.

With more than 20 years' teaching experience, Umbhauer's expertise and classroom experience helps students understand what game theory is and how it can be applied to real life examples. This textbook is suitable for both undergraduate and postgraduate students who study game theory, behavioural economics and microeconomics.

Chapter 1
How to build a game

Introduction

What is game theory and what do we expect from it? One way to present game theory is to say that this theory aims to study the interactions between agents that are conscious of their interaction. But of course, this is not specific to game theory given that most social sciences follow the same aim. So, what distinguishes game theory from other social sciences? Rationality of the players? Not so sure. A large part of game theory studies interaction in evolutionary contexts where players only partly understand what is good for them. I would say that the specificity of game theory is the way it structures a context, that is to say the way a game is written. Game theory structures an interactive context in a way that helps to find actions – strategies – with specific properties. It automatically follows that different economic, political, management and social contexts may have the same game theoretic structure and therefore will be studied in a similar way. That is why the beginning of this book looks at the structure of a game, at the way to build it. Structuring an interactive context as a game does not mean solving it – this will be discussed in the following chapters. But building and solving are linked activities. First, the structure often “talks a lot”, in that it helps underline the specificities of a game. Second, you structure with the aim of solving the game, so you eliminate all that is not necessary to find the solutions. This means that you have a good idea of what is and isn’t important for solving a game.

Consequently, building a context as a game is both a fruitful and critical activity. In this chapter we aim to highlight these facts by giving all the elements of the structure of a game. In the first section, we talk about the two main representations of a game: the strategic form game and the extensive form game. In section 2, we turn to a central concept of game theory, the notion of strategy: we develop pure, mixed and behavioural strategies. In section 3 we discuss the concept of information and the way utilities are assigned to the different ways to play the game. We conclude with what can be omitted in a game.

1 Strategic or Extensive Form Games?

If you ask a student about what game theory is, s/he will usually suggest a matrix with a small number of rows and columns, usually 2! Well, this follows from the fact that very often, game theory books and lectures start with strategic form games that can be represented by a matrix with only two rows and two columns. Very often, students only discover extensive form games very late. We will not proceed in the same way. Throughout the book we study strategic form and extensive form games together and highlight the links but also the differences between these two ways to represent a game.

1.1 Strategic/normal form games

1.1.1 Definition

Definition 1. A strategic form game or normal form game¹ is defined by three elements:

N, the set of players, with Card N=N>1

S=XS_i, where S_i is the strategy set of player i, i from 1 to N.

N preference relations, one for each player, defined on S. These relations are supposed to be Von Neumann Morgenstern (VNM), and are therefore usually replaced by VNM utility functions.

What is a strategy and a VNM utility function? For now, we say that a strategy set is the set of all possible actions a player can choose and we define a VNM utility function as a function that not only orders the different outcomes of a game (in terms of preferences) but that also takes into account the way people cope with risk (we will be more precise in section 3).

The strategic form game, if there are less than four players and if the strategy sets are finite, is often represented in a matrix or a set of matrices, where the rows are the first player’s strategies, the columns the second player’s strategies and the matrices the third player’s strategies. It usually follows that very easy – often 2×2 – matrices focus the students’ attention, because they are not difficult and because they can express some nice story games, often quoted in the literature. Well, these story games, that perhaps unfortunately characterize what people usually know from game theory, express some interesting features of interaction that deserve attention and help to illustrate the notion of a strategic form (or normal form) game. So let us present some of them.

1.1.2 Story strategic/normal form games and behavioural comments

Prisoner’s dilemma

In the prisoner’s dilemma game two criminals in separate rooms can choose to deny the implication of both in a crime (they choose to cooperate), or they can say that only the other is implied in the crime (they choose to denounce). The interesting point of this story lies in the pronounced sentences: one year jail for each if both cooperate (the fact that both cooperate is doubtful), no punishment for the denouncer and 15 years for the cooperator if one player cooperates and the other denounces, 10 years for both if they both denounce. Of course these sentences are a little strange (we are not sure that having two doing a crime diminishes the sentence (!), and normally doubts are not enough to convict someone) but they make the story interesting.

Let us write the game in strategic form: Card N=2, S_i={C, D}, i=1, 2, where C and D respectively mean that the player cooperates and denounces. Given the sentences, player 1’s preferences are given by: (D, C)>(C, C)>(D, D)>(C, D) (by convention, the first and second coordinates of a couple are respectively player 1’s and player 2’s actions); player 2’s preferences are symmetric.

By translating these preferences in utilities, the strategic form can be summarized in the following 2×2 Matrix 1.1:

with 1>u>v>0 and 1>u’>v’>0.

Let the game talk: this game raises a dilemma. Both players perfectly realize that they would be better off both cooperating than both denouncing (u>v and u’>v’ – one year jail is better than 10) but they also realize that, whatever is done by the other player – even if he cooperates – one is better off denouncing him (because 1>u and v>0, and 1>u’ and v’>0). As a matter of fact, if your accomplice denounces you, it is quite logical that it is better for you to denounce him also (10 years’ jail is better than 15), but, even if he cooperates, it is better for you to denounce him because no punishment is better than one year jail! So what will happen?

If the story seems rather amazing with respect to actual legal sentences, it is highly interesting because it corresponds to many economic situations. For example, the prisoner’s dilemma is used to illustrate overexploitation of resources (both players are better off not overexploiting a resource (strategy C), but individually it is always better to exploit a resource more rather than less). This game also illustrates the difficulty of contributing to a public investment: it is beneficial for both players that both invest in a public good, but it is always better individually to invest in a private good (even if the other invests in the public good). These situations are called free rider contexts. Bertrand price games also belong to this category. Both sellers are better off coordinating on a high price (C), but each is better off proposing a lower price (D) than the price of the other seller, in order to get the whole market. And so on…

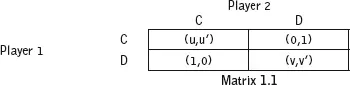
Chicken game, hawk-dove game, and syndicate game

The chicken and the hawk-dove games are strategically equivalent (see section 3 for a more nuanced point of view) in that they (at least seemingly) lead to the same strategic form.

In the chicken game two – stupid – drivers drive straight ahead in opposite directions and rush at the opponent. If nobody swerves, there is a dramatic accident and both die. If one driver swerves (action A) whereas the other goes straight on (action B), the one who swerves is the big...

Table of contents

• Cover
• Title
• Copyright
• Dedication
• Contents
• Acknowledgements
• Introduction
• 1 HOW TO BUILD A GAME
• 2 DOMINANCE
• 3 NASH EQUILIBRIUM
• 4 BACKWARD INDUCTION AND REPEATED GAMES
• 5 TREMBLES IN A GAME
• 6 SOLVING A GAME DIFFERENTLY
• ANSWERS TO EXERCISES
• Index