The Audio Expert

Everything You Need to Know About Audio

Ethan Winer

• Publisher: Routledge
• Year: 2017
• ISBN:
  9781351840064
• Edition: 2
• Topic: Technology & Engineering
• Subtopic: Acoustical Engineering
• Index: Technology & Engineering

The Audio Expert is a comprehensive reference book covering all aspects of audio, with both practical and theoretical explanations. It is written for people who want to understand audio at the deepest, most technical level, but without needing an engineering degree. The Audio Expert explains how audio really works in much more depth than usual, using common sense plain-English explanations and mechanical analogies, with minimal math. It uses an easy to read conversational tone, and includes more than 400 figures and photos to augment the printed text.

However, this book goes beyond merely explaining how audio works. It brings together the concepts of audio, aural perception, musical instrument physics, acoustics, and basic electronics, showing how they're intimately related. It also describes in great detail many practices and techniques used by recording and mixing engineers, including video production and computers. This book is meant for intermediate to advanced recording engineers and audiophiles who want to become experts. There's plenty for beginners too.

One unique feature is explaining how audio devices such as equalizers, compressors, and A/D converters work internally, and how they're spec'd and tested, rather than merely describing how to use them. There's plenty of myth-busting and consumerism too. The book doesn't tell readers what brand power amplifier to buy, but it explains in great detail what defines a good amplifier so people can choose a first-rate model wisely without over-paying.

Most explanations throughout the book are platform-agnostic, applying equally to Windows and Mac computers, and to most software and hardware. Many audio and video examples are included to enhance the written text.

The new edition offers many updates and improvements throughout. New sections on coding an equalizer, comparing microphone preamps, testing results of loudspeaker isolation devices, new online video content on music theory, plus incorporated chapters on MIDI basics, computers, video production, plus new myth-busters, and much more!

Part 1

Audio Defined

If a tree falls in the forest and no one is there to hear it, does it make a sound?

I hope it’s obvious that the answer to the preceding question is yes, because sounds exist in the air whether or not a person, or a microphone, is present to hear them. At its most basic, audio is sound waves—patterns of compression and expansion that travel through a medium such as air—at frequencies humans can hear. Therefore, audio can be as simple as the sound of someone singing or clapping her hands outdoors or as complex as a symphony orchestra performing in a reverberant concert hall. Audio also encompasses the reproduction of sound as it passes through electrical wires and circuits. For example, you might place a microphone in front of an orchestra, connect the microphone to a preamplifier, which then goes to a tape recorder, which in turn connects to a power amplifier, which is finally sent to one or more loudspeakers. At every stage as the music passes through the air to the microphone, and on through the chain of devices, including the connecting wires in between, the entire path is considered “audio.”

Chapter 1

Audio Basics

When you can measure what you are speaking about, and express it in numbers, you know something about it; but when you cannot measure it, when you cannot express it in numbers, your knowledge is of a meager and unsatisfactory kind; it may be the beginning of knowledge, but you have scarcely in your thoughts advanced to the state of science.

—Lord Kelvin (Sir William Thomson), nineteenth-century physicist

Volume and Decibels

When talking about sound that exists in the air and is heard by our ears (or picked up by a microphone), volume level is referred to as sound pressure level, or SPL. Our ears respond to changing air pressure, which in turn deflects our eardrums, sending the perception of sound to our brains. The standard unit of measurement for SPL is the decibel, abbreviated dB. The “B” refers to Alexander Graham Bell (1847–1922), and the unit of measure is actually the Bel. But one Bel is too large for most audio applications, so one-tenth of a Bel, or one decibel, became the common unit we use today.

By definition, decibels express a ratio between two volume levels, but in practice SPL can also represent an absolute volume level. In that case there’s an implied reference to a level of 0 dB SPL—the softest sound the average human ear can hear, also known as the threshold of hearing. So when the volume of a rock concert is said to be 100 dB SPL when measured 20 feet in front of the stage, that means the sound is 100 dB louder than the softest sound most people can hear. Since SPL is relative to an absolute volume level, SPL meters must be calibrated at the factory to a standard acoustic volume.

For completeness, 0 dB SPL is equal to a pressure level of 20 micropascals (millionths of 1 Pascal, abbreviated μPa). Like pounds per square inch (PSI), the Pascal is a general unit of pressure—not only air pressure—and it is named in honor of the French mathematician Blaise Pascal (1623–1662).

Note that decibels use a logarithmic scale, which is a form of numeric “compression.” Adding dB values actually represents a multiplication of sound pressure levels, or voltages when it relates to electrical signals. Each time you add some number of decibels, the underlying change in air pressure, or volts for audio circuits, increases by a multiplying factor:

• +6 dB = 2 times the air pressure or volts
• +20 dB = 10 times the air pressure or volts
• +40 dB = 100 times the air pressure or volts
• +60 dB = 1,000 times the air pressure or volts
• +80 dB = 10,000 times the air pressure or volts

Likewise, subtracting decibels results in division:

• −6 dB = 1/2 the air pressure or volts
• −20 dB = 1/10 the air pressure or volts
• −40 dB = 1/100 the air pressure or volts
• −60 dB = 1/1,000 the air pressure or volts
• −80 dB = 1/10,000 the air pressure or volts

So when the level of an acoustic source or voltage increases by a factor of 10, that increase is said to be 20 dB louder. But increasing the original level by 100 times adds only another 20 dB, and raising the volume by a factor of 1,000 adds only 20 dB more. Using decibels instead of ratios makes it easier to describe and notate the full range of volume levels we can hear. The span between the softest sound audible and the onset of extreme physical pain is about 140 dB. If that difference were expressed using normal (not logarithmic) numbers, the span would be written as 10,000,000,000,000 to 1, which is very unwieldy! Logarithmic values are also used because that’s just how our ears hear. An increase of 3 dB represents a doubling of power,¹ but it sounds only a little louder. To sound twice as loud, the volume needs to increase by about 8 to 10 dB, depending on various factors, including the initial volume and the frequencies present in the source.

Note that distortion and noise specs for audio gear can be expressed using either decibels or percents. For example, if an amplifier adds 1 percent distortion, that amount of distortion could be stated as being 40 dB below the original signal. Likewise, noise can be stated as a percent or dB difference relative to some output level. Chapter 2 explains how audio equipment is measured in more detail.

You may have read that the smallest volume change people can hear is 1 dB. Or you may have heard it as 3 dB. In truth, the smallest level change that can be noticed depends on several factors, including the frequencies present in the source. We can hear smaller volume differences at midrange frequencies than at very low or very high frequencies. The room you listen in also has a large effect. When a room is treated with absorbers to avoid strong reflections from nearby surfaces, it’s easier to hear small volume changes because echoes don’t drown out the loudspeaker’s direct sound. In a room outfitted with proper acoustic treatment, most people can easily hear level differences smaller than 0.5 dB at midrange frequencies.

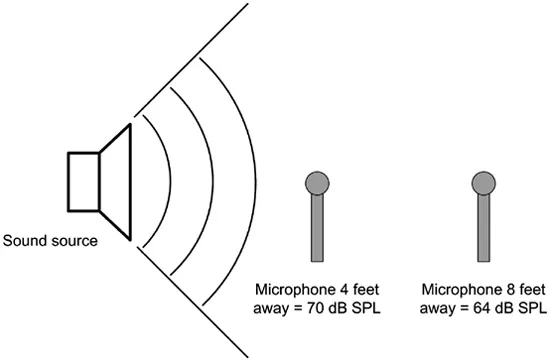
It’s also worth mentioning the inverse square law. As sound radiates from a source, it becomes softer with distance. This decrease is due partly to absorption by the air, which affects high frequencies more than low frequencies, as shown in Table 1.1. But the more important reason is simply because sound radiates outward in an arc, as shown in Figure 1.1. Each time the distance from a sound source is doubled, the same amount of energy is spread over an area twice as wide. Therefore, the level reduces by a corresponding amount, which in this case is 6 dB.

Table 1.1: Frequencies over Distances at 20°C (68°F) with a Relative Humidity of 70%

Frequency	Attenuation Over Distance
125 Hz	0.3 dB/Km
250 Hz	1.1 dB/Km
500 Hz	2.8 dB/Km
1,000 Hz	5.0 dB/Km
2,000 Hz	9.0 dB/Km
8,000 Hz	76.6 dB/Km

Figure 1.1: Sound radiates outward from a source in an arc, so its volume is reduced by 6 dB with each doubling of distance. As you can see in Table 1.1, very high frequencies are reduced over distances due to absorption by the air. This attenuation is in addition to losses caused by the inverse square law, which applies equally to all frequencies.

Standard Signal Levels

As with acoustic volume levels, the level of an audio signal in a wire or electrical circuit is also expressed in decibels, either relative to another signal or relative to one of several common standard reference levels. An amplifier that doubles its input voltage is said to have a gain of 6 dB. This is the same amount of increase whether the input is 0.001 volts or 5 volts; at any given moment, the output voltage is twice as large as the input voltage. But, as with SPL, the dB is also used to express absolute levels for electronic signals using a chosen reference. The most common metrics for expressing volume levels in audio devices are dBu, dBm, dBV, and dBFS.

Most professional audio gear currently manufactured specifies input and output levels as dBu, with 0 dBu corresponding to 0.775 volts. This seemingly unusual voltage is not arbitrary because it relates to the earlier dBm standard described next. The “u” in dBu stands for “unloaded” (or, in some earlier usage, “unterminated”) because the levels are not dependent on a specific load impedance, or termination. Other dBu values describe levels either lower or higher than the 0.775 volt 0 dBu reference. For example, 20 dBu is 10 times larger at 7.75 volts, and −10 dBu is about one third smaller at only 0.245 volts. The volume unit (VU) meters in a recording studio or broadcast console are also offset by convention. When calibrating VU meters, a technician typically uses a 1 KHz sine wave at +4 dBu (1.23 volts). So when that level appears at an input or output connector, the console’s meter reads 0 VU.

The “m” in dBm stands for milliwatt, with 0 dBm equal to 1 milliwatt (thousandth of a watt) of power. The dBm is mostly obsolete, but its history is important because the current dBu standard is derived from dBm, which is a measure of power rather than voltage. Years ago audio systems were designed to transfer as much power as possible from one device to another. Modern audio systems instead transfer voltage, which is much more efficient and uses a different input and output scheme. Therefore, dBu relates only to volts, regardless of the input and output impedance of the connected devices. Volts, watts, and impedance are explained in much more depth in later chapters. But for now, the value 0.775 is used because telephone systems and older audio devices were designed with an input and output impedance of 600 ohms. In that case 1 milliwatt of power is dissipated when 0.775 volts is applied to a 600 ohm load. So dBm and dBu values are often the same, but dBm applies only when the input and output devices have a 600 ohm impedance.

Another standard is dBV, where the “V” stands for volts. References to dBV are less common with professional devices, but they’re sometimes used for consumer electronics. With this standard, 0 dBV equals 1 volt, so by extension 20 dBV equals 10 volts and −6 dBV is half a volt. Since a value of 0 dBV equals 1.0 volt versus 0.775 volts for 0 dBu, the 0.225-volt disparity yields a constant difference of 2.21 dB. And since dBV is referenced to a larger value, it will always be a smaller number than dBu for the same signal level.

The unit dBFS is specific to digital audio, where FS means Full Scale. This is the maximum level a digital device can accommodate or, more accurately, the largest equivalent digital number a sound card or A/D/A converter can accept or output. Once an audio signal has been digitized, no reference voltage level is needed or implied. Whatever input and output voltage your particular sound card or outboard converter is calibrated for, 0 dBFS equals the maximum internal digital level possible before the onset of gross distortion.

One more item related to basic signal levels is the difference between a peak level and an average level, which is also called RMS level. The voltage of any waveform, or any varying or static audio signal, can be expressed as either a peak or average value. Figure 1.2 shows three basic waveforms: sine, square, and pulse. I added shading inside each wave to convey the mathematical concept of “area under the curve,” which represents the amount of energy each wave shape contains. When recording audio we usually care most about the maximum or peak level, because that’s what determines where the audio will become distorted. But the perceived loudness of music or other sound is related to its average level.

The square wave in this example always contains either plus 1 volt or minus 1 volt, where the pulse wave is active only about 20 percent of the time. So the square wave sounds louder than the pulse wave even though both have the same peak value of 1 volt. The average level for the pulse wave is about 8 dB lower too. In this case “average” is in part a theoretical concept because it requires averaging every possible voltage that exists over time, which in theory is an infinite number of values. But the concept should be clear enough even if you consider only a few of the values within the shaded areas. The average level of the pulse wave depends entirely on its peak voltage and “on and off” times, but the sine wave changes constantly over time, so that requires averaging all the voltages. And since energy and loudness are independent of polarity, positive and negative voltages are both treated as positive values.

Finally, RMS is an...