
- 305 pages
- English
- ePUB (mobile friendly)
- Available on iOS & Android
A Laboratory Manual in Biophotonics
About this book
Biophotonics is a burgeoning field that has afforded researchers and medical practitioners alike an invaluable tool for implementing optical microscopy. Recent advances in research have enabled scientists to measure and visualize the structural composition of cells and tissue while generating applications that aid in the detection of diseases such as cancer, Alzheimer's, and atherosclerosis. Rather than divulge a perfunctory glance into the field of biophotonics, this textbook aims to fully immerse senior undergraduates, graduates, and research professionals in the fundamental knowledge necessary for acquiring a more advanced awareness of concepts and pushing the field beyond its current boundaries. The authors furnish readers with a pragmatic, quantitative, and systematic view of biophotonics, engaging such topics as light-tissue interaction, the use of optical instrumentation, and formulating new methods for performing analysis. Designed for use in classroom lectures, seminars, or professional laboratories, the inclusion and incorporation of this textbook can greatly benefit readers as it serves as a comprehensive introduction to current optical techniques used in biomedical applications.
- Caters to the needs of graduate and undergraduate students as well as R&D professionals engaged in biophotonics research.
- Guides readers in the field of biophotonics, beginning with basic concepts before proceeding to more advanced topics and applications.
- Serves as a primary text for attaining an in-depth, systematic view of principles and applications related to biophotonics.
- Presents a quantitative overview of the fundamentals of biophotonic technologies.
- Equips readers to apply fundamentals to practical aspects of biophotonics.
Frequently asked questions
- Essential is ideal for learners and professionals who enjoy exploring a wide range of subjects. Access the Essential Library with 800,000+ trusted titles and best-sellers across business, personal growth, and the humanities. Includes unlimited reading time and Standard Read Aloud voice.
- Complete: Perfect for advanced learners and researchers needing full, unrestricted access. Unlock 1.4M+ books across hundreds of subjects, including academic and specialized titles. The Complete Plan also includes advanced features like Premium Read Aloud and Research Assistant.
Please note we cannot support devices running on iOS 13 and Android 7 or earlier. Learn more about using the app.
Information
(1.1) |
|---|
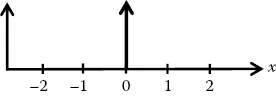
(1.2) |
|---|
(1.3) |
|---|
(1.4) |
|---|
(1.5) |
|---|
(1.6) |
|---|
(1.7) |
|---|
(1.8) |
|---|
(1.9) |
|---|
(1.10) |
|---|
(1.11) |
|---|
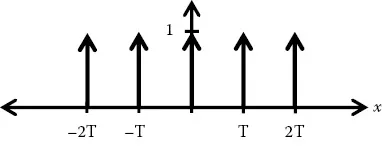

(1.12) |
|---|
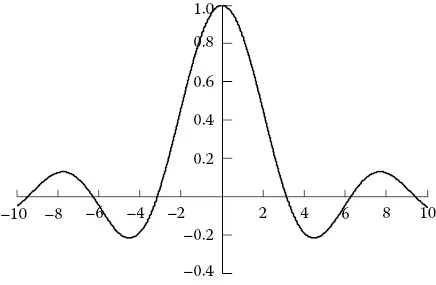
(1.13) |
|---|
(1.14) |
|---|
(1.15) |
|---|
Table of contents
- Cover
- Half Title
- Title Page
- Copyright Page
- Contents
- Preface
- Authors
- 1. General Introductory Topics
- 2. Optics Components and Electronic Equipment
- 3. Fundamental Light–Tissue Interactions: Light Scattering and Absorption
- 4. Microscopic Tissue Imaging
- 5. Tissue Spectroscopy
- 6. Computational Biophotonics
- Index