A Focus on Multiplication and Division

Bringing Research to the Classroom

Elizabeth T. Hulbert, Marjorie M. Petit, Caroline B. Ebby, Elizabeth P. Cunningham, Robert E. Laird

• Publisher: Routledge
• Year: 2017
• Print ISBN: 9781138205680
• eBook ISBN: 9781351671699
• Edition: 1
• Topic: Education
• Subtopic: Education General

A Focus on Multiplication and Division is a groundbreaking effort to make mathematics education research readily accessible and understandable to pre- and in-service K–6 mathematics educators. Revealing students' thought processes with extensive annotated samples of student work and vignettes characteristic of teachers' experiences, this book is sure to equip educators with the knowledge and tools needed to modify their lessons and to improve student learning of multiplication and division.

Special Features:

• Looking Back Questions at the end of each chapter allow teachers to analyze student thinking and to consider instructional strategies for their own students.

• 
  
  

• Instructional Links help teachers relate concepts from each chapter to their own instructional materials and programs.

• 
  
  

• Big Ideas frame the chapters and provide a platform for meaningful exploration of the teaching of multiplication and division.

• 
  
  

• Answer Key posted online offers extensive explanations of in-chapter questions.

• 
  
  

Each chapter includes sections on the Common Core State Standards for Mathematics and integrates the Ongoing Assessment Project (OGAP) Multiplicative Reasoning Progression for formative assessment purposes. Centered on the question of how students develop their understanding of mathematical concepts, this innovative book places math teachers in the mode of ongoing action researchers.

1
What Is Multiplicative Reasoning?

Big Ideas

• Although students may use repeated addition or subtraction to solve multiplication or division problems, multiplication and division are not simply an extension of addition and subtraction.
• Multiplicative reasoning is about understanding situations where multiplication or division is an appropriate operation and having a variety of skills and concepts to approach those situations flexibly.
• There are a number of skills and concepts that a student must understand in order to be fluent with multiplication and division.
• Strong multiplicative reasoning involving whole numbers provides the foundation for fractional and proportional reasoning.

Multiplicative reasoning is a cornerstone to success in other mathematical topics and a potential gatekeeper to success both in and out of school. Multiplicative reasoning is foundational for the understanding of many of the mathematical concepts that are encountered later in students’ school career, such as ratios, fractions, and linear functions, as well as in everyday situations (Vergnaud, 1983). In this chapter multiplicative reasoning is described in two ways: 1) mathematically and 2) from a teaching and learning perspective.

Multiplicative Reasoning: The Mathematics

“Multiplicative reasoning is a complicated topic because it takes different forms and deals with many different situations” (Nunes & Bryant, 1996, p. 143). In elementary school, for example, students engage in a range of multiplication and division contexts, including equal groups, equal measures, unit rates, measurement conversions, multiplicative comparisons, scaling, and area and volume. The types of quantities involved and how the quantities interact are key to understanding multiplication and division in these different contexts. In this chapter the general concept of initial multiplicative understanding is examined. Chapter 5 provides an in-depth discussion of each of these contexts and how they affect student strategies and reasoning.

This section focuses on the following:

1. Why multiplication and division are not simply an extension of addition and subtraction:
   • How the number relationships in addition are different from those in multiplication.
   • How the actions in addition are different from those in multiplication.
2. The difference between additive (absolute) reasoning and multiplicative (relative) reasoning.

There is a commonly held belief among many educators that multiplication and division are just extensions of addition and subtraction. This belief arises because it is possible to solve whole number multiplication and division problems using repeated addition and subtraction, respectively. However, multiplication and division involve a different set of number relationships and different actions than addition and subtraction, which are described next.

Number Relationships and Actions in Addition

Additive reasoning involves situations in which sets of objects are joined, separated, or compared. For example, 3 apples + 6 apples = 9 apples. Each apple is a separate entity, and the sum is the union of all the apples as shown in Figure 1.1. It is also important to remember that in additive situations the numbers tell the actual size of each set. So in the case of 3 apples + 6 apples, the 3 means how many in one set and the 6 means how many in another set. The numbers in additive situations represent the value of each of the independent sets and do not rely on the other number for meaning or value. As you will see, this is not the case with multiplication and division.

Figure 1.1 The sum of 3 apples and 6 apples is 9 apples (3 apples + 6 apples = 9 apples).

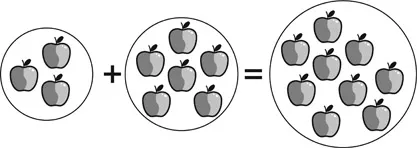
Number Relationships and Actions in Multiplication

One major difference between additive reasoning and multiplicative reasoning is that multiplicative reasoning does not involve the actions of joining and separating, but instead, it often involves the action of iterating, or making multiple copies, of a unit. Instead of involving one-to-one correspondence (1 apple) as in additive reasoning, multiplication often involves many-to-one correspondence (Nunes & Bryant, 1996). It is important to note that the examples used in this section are equal group problems, one of the first many-to-one situations that elementary students encounter in instruction.

To understand what is meant by this many-to-one correspondence, consider a plate with 3 apples. One plate has 3 apples, so the many-to-one relationship is 3 apples to 1 plate. When you increase the number of plates, you increase the number of apples by the number of apples on each plate. The constant relationship of 3 apples to 1 plate, however, never changes. When thinking about answering the question how many apples on 6 plates, you can think of this as 6 iterations of 3 apples to 1 plate. Figure 1.2 shows the 3 apples per plate iterated 6 times (once for each plate of 3 apples).

6 plates × 3 apples on each plate = 18 apples

Figure 1.2 Six times 3 apples on each plate equals 18 apples. That is, the composite unit of 3 apples to one plate is iterated 6 times (6 plates × 3 apples in each plate = 18 apples).

Notice that the number of apples is scaled up or down depending on the number of plates. The number of iterations of the composite unit (e.g., 3 apples to each plate; 3 apples per plate) called for in a problem can also be thought of as the scalar factor. In the case of Figure 1.2, the scalar factor is 6, meaning that the composite unit of 3 (apples per plate) is iterated 6 times, resulting in a product of 18 apples.

Researchers refer to the many-to-one relationship as the composite unit. Students who see, iterate, and operate with the composite unit are unitizing. Unitizing refers to the understanding that quantities can be grouped and then the group can be referred to as one unit yet have a value greater than 1. Imagine a package of 4 cookies. The unit is the package, but the package has a value of 4 cookies. There is a more detailed discussion of this idea in Chapter 4. Conceptually it is harder for children to mentally keep track of a composite unit than it is to count by ones, as they must coordinate two levels of units (the composite unit and the number of units you count by) (Steffe, 1992; Ulrich, 2015).

Students who first begin to unitize may solve multiplication problems by iterating the composite unit using repeated addition instead of multiplication. This evidence often leads one to think that multiplication is an extension of addition. However, what distinguishes repeated addition in a multiplicative situation from additive reasoning is the composite unit (many-to-one) is iterated and added. When students develop more sophisticated multiplicative reasoning, they can conceptualize 18 as being made up of 6 composite units of 3 individual units each.

As students develop their understanding and flexibly use unitizing, they will move away from the repeated addition strategy to strategies that involve multiplication. Consider Lyla’s explanation:

“Well, I know that 8 × 8 is 64 so to find 8 × 7 I just need to take 1 away—I mean 1 row of 8 away—and that would be 56.”

In explaining her strategy for finding the product of 8 and 7, Lyla uses language that indicates an understanding of unitizing. Note Lyla’s reference to removing a row. Iterations of a composite unit can take many visual forms. Some of these may be one column or row in an array iterated multiple times or one group in a set iterated multiple times. Lyla’s explanation helps to make sense of what happens when one of the numbers in a multiplication situation is changed. Changing the value of either the composite unit or the scalar factor has an impact on the total by the value of the other number.

Consider the situation of 6 plates with 3 apples per plate again. By decreasing the number of plates to 5, the number of apples decreases by one composite unit, or 1 plate of 3 apples. See Figure 1.3.

In multiplication the quantities are different from each other and yet dependent on each other. In this example the total number of apples is dependent on the number of plates. This understanding represents a significant difference between addition and multiplication.

Figure 1.3 Five plates × 3 apples in each plate is 3 apples (one composite unit) less than 6 plates × 3 apples in each plate.

Students who reason multiplicatively can unitize, or see a composite unit, and then create multiple copies of it. As stated earlier, however, this is just the beginning of considering the meaning of multiplication in a very complex landscape. Although initially an understanding of multiplication is reliant on students making multiple copies, or iterations, of that composite unit, eventually we need students to broaden their multiplicative reasoning to include more complex actions and contexts. These will be discussed in detail throughout this book. A summary of the difference in number relationships and actions between additive and multiplicative situations discussed in this section is found in Table 1.1.

Table 1.1 Differences between additive and multiplicative reasoning discussed in this section.

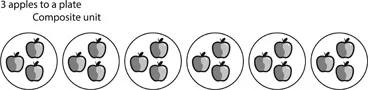
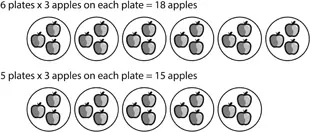
	Number Relationships	Actions
Additive Reasoning	One-one correspondence	Joining, separating, or comparing
Multiplicative Reasoning	Many-to-one composite unit	Iterating and scaling

Absolute and Relative Differences

Another way to think about the difference between additive reasoning and multiplicative re...

Table of contents

• Cover
• Title
• Copyright
• Dedication
• Contents
• Preface
• Acknowledgments
• 1 What Is Multiplicative Reasoning?
• 2 The OGAP Multiplication Progression
• 3 The Role of Visual Models
• 4 The Role of Concepts and Properties
• 5 Problem Contexts
• 6 Structures of Problems
• 7 Developing Whole Number Division
• 8 Understanding Algorithms
• 9 Developing Math Fact Fluency
• References
• About the Authors
• Index