Encyclopedic Handbook of Integrated Optics

Kenichi Iga, Yasuo Kokubun

• Publisher: CRC Press
• Year: 2018
• Print ISBN: 9780824724252
• eBook ISBN: 9781351836838
• Topic: Physical Sciences
• Subtopic: Optics & Light

As optical technologies move closer to the core of modern computer architecture, there arise many challenges in building optical capabilities from the network to the motherboard. Rapid advances in integrated optics technologies are making this a reality. However, no comprehensive, up-to-date reference is available to the technologies and principles underlying the field. The Encyclopedic Handbook of Integrated Optics fills this void, collecting the work of 53 leading experts into a compilation of the most important concepts, phenomena, technologies, and terms covering all related fields.

This unique book consists of two types of entries: the first is a detailed, full-length description; the other, a concise overview of the topic. Additionally, the coverage can be divided into four broad areas:

A survey of the basics of integrated optics, exploring theory, practical concerns, and the fundamentals behind optical devices

Focused discussion on devices and components such as arrayed waveguide grating, various types of lasers, optical amplifiers, and optoelectronic devices

In-depth examination of subsystems including MEMS, optical pickup, and planar lightwave circuits

Finally, systems considerations such as multiplexing, demultiplexing, 3R circuits, transmission, and reception

Offering a broad and complete treatment of the field, the Encyclopedic Handbook of Integrated Optics is the complete guide to the fundamentals, principles, and applications of integrated optics technology.

O

OPTICAL COUPLING IN WAVEGUIDES

Kazuhito Furuya

The power transfer, that is, the optical or mode coupling is caused by any coupling mechanism between two waves. If such couplings, are not there the multimode fibers would be used as single-mode transmission media by using only one mode to transmit a narrow pulse without any broadening. However, in practice, mode couplings are unavoidable. On the other hand, functional optical devices, such as directional-couplers, switches, etc., use the coupling as their operational principle. The basics of the coupling are described here.

Let us consider optical Waves 1 and 2 of angular frequency ω propagating in the +z direction. Waves 1 and 2 may be waves propagating either along two parallel waveguides 1 and 2 or as two Modes 1 and 2 in a single waveguide. Their amplitudes are a₁(z) and a₂(z), while $P_1\left(z\right)={\left|a_1\left(z\right)\right|}^2$ and $P_2\left(z\right)={\left|a_2\left(z\right)\right|}^2$ are their powers. When there is no coupling, amplitudes are given as

$\begin{array}{cc}{a}_1\left(z\right)=a_{10}\exp \left(-i{\beta }_{1}z\right)& a_2\left(z\right)=a_{20}\exp \left(-i{\beta }_{2}z\right)\end{array},$

where β₁ and β₂ are propagation constants of waves. When there is coupling, the equation can be written as

$\begin{array}{cc}\frac{\text{d}{a}_1}{\text{d}z}=-{\beta }_1{a}_1+C_{12}{a}_2& \frac{\text{d}{a}_2}{\text{d}z}=-{\beta }_2{a}_2+C_{21}{a}_1\end{array},$

(1)

where C₁₂ is the coupling coefficient representing the amplitude transfer from Wave 2 to Wave 1 while C₂₁ is that from Wave 1 to Wave 2. Assuming lossless waveguide, that is, (d/dz) (P₁ + P₂) = 0, condition C₁₂ = –C₂₁^* is derived from Eq. (1). In the following sections, weak coupling thoery, periodic coupling, random coupling, and microbending loss in fibers are described.

WEAK COUPLING THEORY

Assuming that $\left|C_{12}\right|\ll {\beta }_1,{\beta }_2$ (weak coupling) and constant C₁₂, substituting a₁(z) = Aexp(-iβz) and a₂(z) = B exp(–iβz) into Eq. (1) we obtain solutions for β, a₁(z), and a₂(z) as follows:

$\beta ={\beta }_a\pm {\beta }_b,$

where β_a = (β₁ + β₂)/2 (average propagation constant), ${\beta }_b=\sqrt{{\beta }_d{}^2+{\left|C_{12}\right|}^2}$ (beat propagation constant) and β_d = (β₁ – β₂)/2.

$a_1\left(z\right)=\exp \left(-i{\beta }_{a}z\right)\left\{\left(\cos {\beta }_{b}z-i\frac{{\beta }_d}{{\beta }_b}\sin {\beta }_{b}z\right)a_1\left(0\right)+\frac{C_{12}}{{\beta }_b}\sin {\beta }_{b}z{a}_2\left(0\right)\right\},$

$a_2\left(z\right)=\exp \left(-i{\beta }_{a}z\right)\left\{\left(\cos {\beta }_{b}z+i\frac{{\beta }_d}{{\beta }_b}\sin {\beta }_{b}z\right)a_2\left(0\right)+\frac{C_{21}}{{\beta }_b}\sin {\beta }_{b}z{a}_1\left(0\right)\right\},$

Substituting a₁(0) = 1 and a₂(0) = 0 as the initial condition, we obtain

$\begin{array}{ccc}{P}_1\left(z\right)=1-F{\sin }^2{\beta }_{b}z& P_2\left(z\right)=F{\sin }^2{\beta }_{b}z,& \text{where}F=\frac{1}{1+{\left\{\left({\beta }_1-{\beta }_2\right)\text{/}2\left|C_{12}\right|\right\}}^2}\end{array}.$

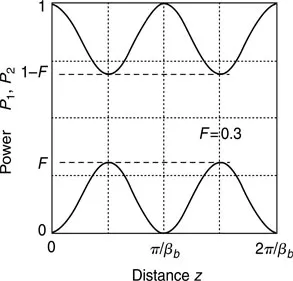
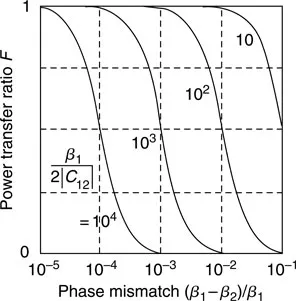
Factor F is the maximum ratio of the power transfered from one wave to the other, to the total power carried by the waves. The maximum transfer takes place at the distance of the coupling length π/2β_b multiplied by an integer. Between the two waves, fractional power is transferred back and forth as shown in Figure 1. When two propagation constants coincide, β₁ = β₂, F is unity (100% power transfer). A relation between F and the mismatch in the propagation constant is shown in Figure 2. This is useful in designing directional coupler type devices.

PERIODIC COUPLING

When β₁ ≠ β₂ and the coupling coefficients are periodic functions with the period $2\pi \text{/}\left|{\beta }_1-{\beta }_2\right|$ as

$\begin{array}{cc}{C}_{12}=iC\exp \left(-i\left({\beta }_1-{\beta }_2\right)z\right)& C_{21}=iC\exp \left(i\left({\beta }_1-{\beta }_2\right)z\right)\end{array},$

100% power transfer takes place. These satisfy the lossless condition C₁₂ = –C₂₁^*. This is shown by substituting the previous and the following equation

$\begin{array}{cc}{a}_1\left(z\right)=A_1\left(z\right)\exp \left(-i{\beta }_{2}z\right)& a_2\left(z\right)=A_2\left(z\right)\exp \left(-i{\beta }_{2}z\right)\text{into Eq}\text{.}\left(1\right)\text{to obtain}\end{array}$

$\begin{array}{cc}{a}_1\left(z\right)=a_1\left(0\right)\cos Cz\exp \left(-i{\beta }_{1}z\right)& a_2\left(z\right)=i{a}_1\left(0\right)\sin Cz\exp \left(-i{\beta }_{2}z\right)\end{array}.$

RANDOM COUPLING

In multimode waveguides, for example, multimode fibers, even if single mode is excited, after the propagation, the power distributes over multiple modes by the mode coupling. The cause of the coupling is imperfect homogeneity of the waveguide structure along the axial direction [1,2], for example, as a result of bending of the fiber axis. Such a coupling mechanism varies at random along the axial direction.

Figure 1 Powers in Waves 1 and 2 versus propagation distance

Figure 2 Power transfer ratio versus mismatch in propagation constant

Let us consider that only Wave 1 carries the power at z = 0, β₁ ≠ β₂ and, therefore, the power of Wave 2 is always much smaller than that of Wave 1. Neglecting the second term in the right-hand side of the first equation in Eq. (1) we get

$a_1\left(z\right)=a_1\left(0\right)\exp \left(-i{\beta }_{1}z\right).$

Substituting this into the second equation in Eq. (1)

$a_2\left(z\right)=\exp \left(-i{\beta }_{2}z\right){\displaystyle {\int }_0^z{C}_{21}\left(z^{\prime }\right)a_1\left(0\right)\exp \left(i\left({\beta }_2-{\beta }_1\right)z^{\prime }\right)\text{d}{z}^{\prime }}.$

Since C₂₁(z’) is a statistical function of z’, any deterministic analysis is unavailable.

However, we can obtain P₂(z) as follows:

$P_2\left(z\right)={\left|a_2\left(z\right)\right|}^2$

$={\left|a_1\left(0\right)\right|}^2{\displaystyle {\int }_0^z{\displaystyle {\int }_0^z{C}_{21}\left(z^{\prime }\right)C_{21}^{*}\left(z^{″}\right)\exp \left(i\left({\beta }_2-{\beta }_1\right)z^{\prime }\right)\exp \left(i\left({\beta }_2-{\beta }_1\right)z^{″}\right)\text{d}{z}^{\prime }\text{d}{z}^{″}}}$

$=z{\left|a_1\left(0\right)\right|}^2{\displaystyle {\int }_{-\infty }^{\infty }R\left(u\right)\exp \left(i\left({\beta }_1-{\beta }_2\right)u\right)\text{d}u}$

$=z{\left|a_1\left(0\right)\right|}^{2}S\left({\beta }_1-{\beta }_2\right),$

where R(u) is the autocorrelation function of the function C₂₁(z’), that is,

$R\left(u\right)=\underset{z\text{}\to \infty }{\lim }\frac{1}{z}{\displaystyle {\int }_0^z{C}_{21}\left(z^{\prime }\right)C_{21}^{*}\left(z^{\prime }+u\right)\text{d}{z}^{\prime }}.$

R(u) is symmetric with respect to the origin and decreasing function with $\left|u\right|$. A characteristic length, such as l in R(u) = exp(–(u/l²) for example, is called as the correlation length. Here we assume z ≫ l in the derivation of the earlier formula. S(β) is the Fourier transform of R(u) and is equal to the power spectrum (Wiener–Khinchin’s theorem). Finally, the power of Wave 2 is proportional to the distance, and the power spectral density at β₁ – β₂ is the statistic function of th...

Table of contents

• Cover
• Half Title
• Title Page
• Copyright Page
• Table of Contents
• Preface
• How to Read this Handbook
• Introduction
• A
• D
• E
• F
• I
• L
• M
• N
• O
• P
• Q
• R
• S
• T
• V
• W
• Y
• Contributors/Initial of Chapters
• Index