
- 780 pages
- English
- ePUB (mobile friendly)
- Available on iOS & Android
About this book
This book presents a complete and unified treatment of the fundamental themes of structural mechanics, ranging from the traditional to the most advanced topics, covering mechanics of linear elastic solids, theory of beam systems, and phenomena of structural failure. The book considers explicitly all the static and kenetic operators of structural mechanics with their dual character.Topics relating to structural symmetry are covered in a single chapter while dynamics is dealt with at various points. The logical presentation allows the clear introduction of topics such as finite element methods, automatic calculation of framed beam systems, plate and shell theory, theory of plasticity, and fracture mechanics.Numerous worked examples, exercises with complete solutions and illustrations make it accessible both as a text for students and as a reference for research workers and practicing engineers.
Frequently asked questions
- Essential is ideal for learners and professionals who enjoy exploring a wide range of subjects. Access the Essential Library with 800,000+ trusted titles and best-sellers across business, personal growth, and the humanities. Includes unlimited reading time and Standard Read Aloud voice.
- Complete: Perfect for advanced learners and researchers needing full, unrestricted access. Unlock 1.4M+ books across hundreds of subjects, including academic and specialized titles. The Complete Plan also includes advanced features like Premium Read Aloud and Research Assistant.
Please note we cannot support devices running on iOS 13 and Android 7 or earlier. Learn more about using the app.
Information
1
Introduction
1.1 Preliminary remarks
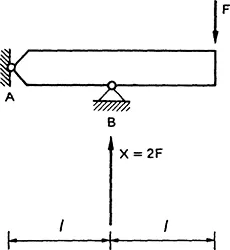
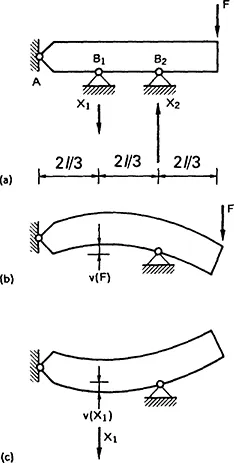
1.1 |
1.2 |
1.3 |
1.2 Classification of structural elements
- one-dimensional elements (e.g. ropes, struts, beams, arches);
- two-dimensional elements (e.g. membranes, plates, slabs, shells, vaults);
- three-dimensional elements (stubby solids).
Table of contents
- Cover Page
- Title Page
- Copyright Page
- Table of Contents
- Preface
- About the Author
- 1 Introduction
- 2 Geometry of areas
- 3 Kinematics and statics of rigid systems
- 4 Determination of constraint reactions
- 5 Internal beam reactions
- 6 Statically determinate beam systems
- 7 Analysis of strain and stress
- 8 Theory of elasticity
- 9 The Saint Venant problem
- 10 Beams and plates in flexure
- 11 Finite element method
- 12 Structural symmetry
- 13 Statically indeterminate structures: method of forces
- 14 Statically indeterminate structures: method of displacements
- 15 Plane frames
- 16 Energy methods for the solution of beam systems
- 17 Instability of elastic equilibrium
- 18 Theory of plasticity
- 19 Plane stress and plane strain conditions
- 20 Mechanics of fracture
- Appendix A Calculation of the internal reactions in a circular arch subjected to a radial hydrostatic load
- Appendix B Calculation of the internal reactions in a circular arch subjected to a uniformly distributed vertical load
- Appendix C Anisotropic material
- Appendix D Heterogeneous beam
- Appendix E Heterogeneous plate
- Appendix F Finite difference method
- Appendix G Torsion of multiply-connected thin-walled cross sections
- Appendix H Shape functions
- Appendix I Application of the Finite Element Method to diffusion problems
- Appendix J Initial strains and residual stresses
- Appendix K Dynamic behaviour of elastic solids with linear damping
- Appendix L Plane elasticity with couple stresses
- Appendix M Rotating circular disk
- Appendix N Thermal stress in a circular disk
- Further reading
- Index