Interaction and Nonlinear Effects in Structural Equation Modeling

Randall E. Schumacker

• Publisher: Routledge
• Year: 2017
• Print ISBN: 9780805829501
• eBook ISBN: 9781351562621
• Topic: Psychology
• Subtopic: History & Theory in Psychology
• Index: Psychology

This volume provides a comprehensive presentation of the various procedures currently available for testing interaction and nonlinear effects in structural equation modeling. By focusing on various software applications, the reader should quickly be able to incorporate one of the procedures into testing interaction or nonlinear effects in their own model. Although every attempt is made to keep mathematical details to a minimum, it is assumed that the reader has mastered the equivalent of a graduate-level multivariate statistics course which includes adequate coverage of structural equation modeling. This book will be of interest to researchers and practitioners in education and the social sciences.

1

A Comparative Review of Interaction and Nonlinear Modeling

Edward E. Rigdon

Georgia State University

Randall E. Schumacker

University of North Texas

Werner Wothke

SmallWaters Corporation, Chicago, Illinois

Interaction effects are common in the real world. A business manager knows that a dollar spent on advertising will yield a greater marginal return in sales for a product with wide distribution than for a product with narrow distribution (Lilien & Kotler, 1983). In contrast, an interaction may dampen the individual effects of the two variables, as when two noises combine to create a zone of apparent quiet. Two gases may be relatively harmless when released into the atmosphere separately, but may yield lethal toxins when released together. Smith and Sasaki (1979) described a “consistency” interaction effect. When two variables both deviate from their means in the same direction, their joint effect is enhanced, but if the deviations are in opposite directions, then the interaction effect is opposite, as well.

Techniques for representing and testing interaction effects are familiar in the regression and analysis-of-variance methodologies. In structural equation modeling (SEM), researchers have a choice of two basic techniques. If one or both of the interacting variables is discrete, or can be made so, researchers can apply a “multisample” approach, with the interaction effects becoming apparent as differences in parameter estimates when the same model is applied to different but related sets of data. If both interacting variables are continuous, researchers can apply Kenny and Judd’s (1984) indicant product analysis procedure for modeling the interaction in a single sample, although this procedure can lead to a number of practical and statistical problems. Because of those problems, researchers have typically either avoided modeling interactions, or else adapted their data to the multisample approach. Recent developments in software, and contributions by Jöreskog and Yang (1996) and Ping (1995), have made it much easier to apply the Kenny and Judd approach, and have provided a fresh look at the statistical issues involved. Consequently, researchers have renewed their interest in the indicant product procedure in SEM.

Unfortunately, the excitement over these developments may have obscured the real relative merits of the multisample and indicant product approaches, in much the same way that earlier excitement over SEM methods in general led some researchers to ignore basic issues (Cliff, 1983). Thus, this may be a good time for a critical comparison of the multisample and indicant product approaches. A careful review suggests that the multisample approach is still the most useful procedure for modeling latent variable interaction effects, under the widest set of circumstances, whereas the indicant product approach should be reserved for particular situations where it will yield superior results.

REVIEW

In general, an interaction effect exists whenever the character of the relationship between variables A and B is affected by the level of variable C (Keppel & Zedeck, 1989). We can demonstrate this by examining a multiple regression equation without interactions:

The first partial derivatives of this equation with respect to B and C describe how a change in the level of one predictor affects the level of A, when the other predictor is held constant. These partial derivatives are, respectively, β₁ and β₂. They show, for example, that the only effect of a change in B on variable A is the “main” effect through β_l. By contrast, consider a regression equation with an interaction term:

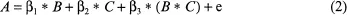
Now the first partial derivatives are β₁ + β₃ * C and β₂ + β₃ * B. In other words, a change in B now affects A not only through B’s main effect but also as a function of the level of C. Accordingly, the main effect of B on A, β₁, can be thought of as an “average” value computed over the range of values for variable C that are represented in the data set (Keppel & Zedeck, 1989).

When researchers suspect an interaction relationship, they may be tempted to avoid SEM altogether, in favor of older techniques such as regression or analysis of variance. The older techniques provide researchers not only with well-established, formal procedures for dealing with interactions, but also with a body of practical experience. These techniques also provide an apparent simplification, because they substantially reduce the number of choices that researchers must make. The disadvantages of this approach, however, are well known. If variables are measured with error, parameter estimates may be biased. Adopting these techniques may reduce the level of rigor in the statistical analysis. Researchers may also find that they need the flexibility of SEM methods to deal with other aspects of their model, even at the cost of substantially increased complexity in dealing with the interaction effect.

The Indicant Product Approach

Kenny and Judd’s (1984) indicant product approach to latent variable interactions involves modeling an “interaction construct,” say ξ₃, which is a function of the “main effect constructs,” ξ₁ and ξ₂. The structural model has the form:

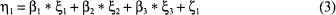
where is the dependent construct and ζ₁ is an error term. The relationship between and ξ₃ is itself linear. The researcher creates ξ₃ so as to represent the kind of nonlinear relationship believed to exist between η₁ and and ξ₂. For example, to model a multiplicative interaction between ξ₁ and ξ_2, ξ₃ must be made equal to ξ₁ * ξ₂. Measures or indicators of ξ₃ are then created as functions of the measures of ξ₁ and ξ₂, in a similar way. Kenny and Judd (1984), Hayduk (1987), and Bollen (1989) have all described the procedure for multiplicative interactions in some detail. It is important to note that the method relies on an external indicator of the hypothesized interaction for model identification.

The Multisample Approach

In the multisample approach, the different samples are defined by the different levels of one or both of the interacting variables. If interaction effects are present, then certain parameters should have different values in different samples (Bagozzi & Yi, 1989, offered a treatment). For example, in the context of an experiment, MacKenzie and Spreng (1992) tested an interaction model of advertising effectiveness. Their model proposed, in part, that a person’s attitude toward an advertisement (A_ad) interacts with the person’s motivation to process the ad (Motivation) to affect the person’s attitude toward the advertised brand (A_brand) (see Figure 1.1). The general structural model may be represented as:

where α is the intercept and ζ is an error term.

MacKenzie and Spreng (1992) hypothesized that subjects in the high-Motivation group would have a higher mean level of A_brand after viewing the ad. This would be reflected in a higher intercept term for the subjects in this condition. They proposed that A_ad should have a positive “main” effect (as represented by β) on A_brand. However, they further proposed that the interaction between A_ad and Motivation would make the A_ad−A_brand relationship weaker in the high-Motivation condition (see Fig. 1.1).

FIG. 1.1. Motivation moderating the intercept and slope of the regression relationship between Attitude toward the Ad and Attitude toward the Brand. (“H” indicates high Motivation and “L” indicates low Motivation.)

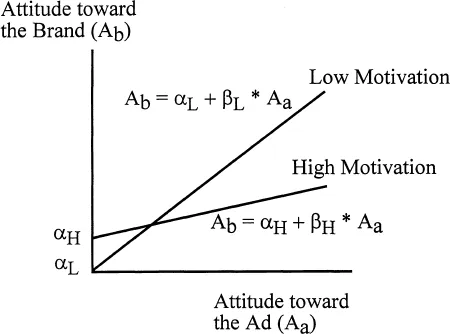
Under the multisample approach, researchers investigate interaction effects using chi-square difference tests. Researchers first estimate a model where the parameters in question are constrained to be equal across the groups, and then estimate a model where the parameters are allowed to differ in the two samples. A significant chi-square difference suggests that the equality constraints are not consistent with the data, and thus that an interaction effect exists.

COMPARATIVE REVIEW

Data Types

A comparative review of the indicant product and multisample approaches should begin with the obvious. The indicant product approach is the “natural” approach when both interacting variables are continuous, whereas the multisampl...

Table of contents

• Cover
• Half Title
• Title Page
• Copyright Page
• Table of Contents
• Preface
• 1 A Comparative Review of Interaction and Nonlinear Modeling
• 2 Modeling Interaction and Nonlinear Effects: A Step-by-Step LISREL Example
• 3 Modeling Interaction and Nonlinear Effects With Mx: A General Approach
• 4 EQS and LISREL Examples Using Survey Data
• 5 Estimating Interaction and Nonlinear Effects With SAS
• 6 Two-Stage Least Squares Estimation of Interaction Effects
• 7 Modeling Interaction Effects: A Two-Stage Least Squares Example
• 8 Effect Decomposition in Interaction and Nonlinear Models
• 9 Estimating Nonlinear Effects Using a Structured Means Intercept Approach
• 10 Estimating Nonlinear Effects Using a Latent Moderated Structural Equations Approach
• 11 Interaction and Nonlinear Modeling: Issues and Approaches
• Author Index
• Subject Index
• About the Authors