Feynman Lectures On Gravitation

Richard Feynman

• Publisher: CRC Press
• Year: 2018
• ISBN:
  9780429982484
• Edition: 1
• Topic: Physical Sciences
• Subtopic: Physics
• Index: Physics

The Feynman Lectures on Gravitation are based on notes prepared during a course on gravitational physics that Richard Feynman taught at Caltech during the 1962-63 academic year. For several years prior to these lectures, Feynman thought long and hard about the fundamental problems in gravitational physics, yet he published very little. These lectures represent a useful record of his viewpoints and some of his insights into gravity and its application to cosmology, superstars, wormholes, and gravitational waves at that particular time. The lectures also contain a number of fascinating digressions and asides on the foundations of physics and other issues.Characteristically, Feynman took an untraditional non-geometric approach to gravitation and general relativity based on the underlying quantum aspects of gravity. Hence, these lectures contain a unique pedagogical account of the development of Einstein's general theory of relativity as the inevitable result of the demand for a self-consistent theory of a massless spin-2 field (the graviton) coupled to the energy-momentum tensor of matter. This approach also demonstrates the intimate and fundamental connection between gauge invariance and the principle of equivalence.

LECTURE 1

1.1 A FIELD APPROACH TO GRAVITATION

In this series of lectures we shall discuss gravitation in all its aspects. The fundamental law of gravitation was discovered by Newton, that gravitational forces are proportional to masses and that they follow an inverse-square law. The law was later modified by Einstein in order to make it relativistic. The changes that are needed to make the theory relativistic are very fundamental; we know that the masses of particles are not constants in relativity, so that a fundamental question is, how does the mass change in relativity affect the law of gravitation.

Now Einstein formulated his law in 1911, so that the subject is not new, and the physical results that we have to explain were beautifully explained by Einstein himself. The usual course in gravitation therefore starts by stating the laws just as Einstein did. This procedure is, however, unnecessary, and for pedagogical reasons we shall here take a different approach to the subject. Today, physics students know about quantum theory and mesons and the fundamental particles, which were unknown in Einstein’s day; physics then consisted simply in gravitation and electrodynamics, and electrodynamics had forced the invention of a theory of relativity, so that the problem was to bring the theory of gravitation into line with the discoveries that had been made by studying electrodynamics.

Einstein’s gravitational theory, which is said to be the greatest single achievement of theoretical physics, resulted in beautiful relations connecting gravitational phenomena with the geometry of space; this was an exciting idea. The apparent similarity of gravitational forces and electrical forces, for example, in that they both follow inverse-square laws, which every kid can understand, made every one of these “kids” dream that when he grew up, he would find the way of geometrizing electrodynamics. Thus a generation of physicists worked trying to make a so-called unified field theory, which would have unified gravitation and electrodynamics into a single thing. None of these unified field theories has been successful, and we shall not discuss them in these lectures. Most of them are mathematical games, invented by mathematically minded people who had very little knowledge of physics, and most of them are not understandable. Einstein himself worked at this, and his writings on the subject at least make some sense, but nevertheless, there is no successful unified field theory that combines gravitation and electrodynamics.

Such a success would have been short lived, however, because now we have so much more in physics than just electrodynamics and gravitation; we would need to worry about unifying mesons and kaons and neutrinos and all the other thirty or so particles that are known. Thus the unification of electrodynamics and gravitation would not have been a grand achievement, since there is so much more in the world besides electricity and gravitation.

Our pedagogical approach is more suited to meson theorists who have gotten used to the idea of fields, so that it is not hard for them to conceive that the universe is made up of the twenty-nine or thirty-one other fields all in one grand equation; the phenomena of gravitation add another such field to the pot, it is a new field which was left out of previous considerations, and it is only one of the thirty or so; explaining gravitation therefore amounts to explaining three percent of the total number of known fields.

We may even describe our approach in terms of a fiction; we imagine that in some small region of the universe, say a planet such as Venus, we have scientists who know all about the other thirty fields of the universe, who know just what we do about nucleons, mesons, etc., but who do not know about gravitation. And suddenly, an amazing new experiment is performed, which shows that two large neutral masses attract each other with a very, very tiny force. Now, what would the Venutians do with such an amazing extra experimental fact to be explained? They would probably try to interpret it in terms of the field theories which are familiar to them.

1.2 THE CHARACTERISTICS OF GRAVITATIONAL PHENOMENA

Before proceeding, let’s review some of the experimental facts which a Venutian theorist would have to play with in constructing a theory for the amazing new effect.

First of all there is the fact that the attraction follows an inversesquare law. For us, this is known very, very accurately from the study of planetary orbits. Then there is the fact that the force is proportional to the masses of the objects. This was known to Galileo, who discovered all objects fall with the same acceleration. How well do we know this? Well, in principle what one should do is quite clear; we first define the mass as the inertia of an object, which we measure by applying known forces and measuring the acceleration. Then we measure the attraction due to gravitation, for example, by weighing, and compare the results. These experiments measuring forces and accelerations would be extremely difficult to perform with sufficient accuracy; but there are other ways of checking this to an accuracy of 1 part in 10⁸, which was first done by Eötvös. One can do this by comparing the gravitational force of the earth with the centrifugal force due to the earth’s rotation, which is a purely inertial effect. In principle, a plumb bob which is at some latitude, not 0° nor 90°, does not point to the center of the earth. Actually it does not point to the center also because of the earth’s bulges, but all this can be taken into account in making the comparison. In any case, at some intermediate angle such as the following: (Figure 1.1) the plumb bob points in a direction which is the resultant of the gravitational force and the centrifugal force. If we now make a plumb bob out of some other material, which has a different ratio of inertial to gravitational mass, it would hang at a slightly different angle. We can thus compare different substances; for example, if we could make the first bob out of copper, and a second one of hydrogen—come to think of it, it would be difficult to make it out of pure hydrogen—(maybe polyethylene would do), we can check the constancy of the ratio of the inertial mass to the gravitational mass

The actual experiment is not done by measuring differences in such tiny angles, but rather by measuring a torque; very small torques are more conveniently measurable because of the peculiar properties of quartz fibers, which can be made very thin and yet be able to support large weights. What is done is to hang two equal weights of the two materials on the ends of a bar, and suspend the bar in an east-west direction at its midpoint; if the component of the forces perpendicular to the gravitational forces are not equal, there is a net torque on the bar, which can be measured. The published results which I have seen, of a recent experiment by Dicke, show no effect, and the conclusion is that the ratio of the inertial masses to the gravitational masses is a constant to an accuracy of one part in 10⁸, for many substances, from oxygen to lead.

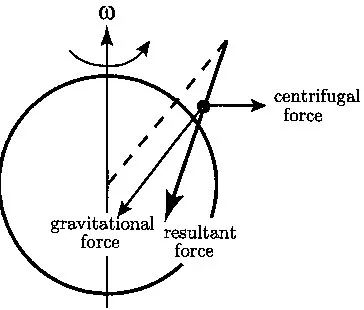
Figure 1.1

A similar experiment may be carried out by comparing the gravitational force due to the sun, to the inertial forces associated with our orbital motion about the sun. After all, here on earth we all are whirling around in space at a fantastic speed along the orbit of the earth, and the only reason we do not notice the motion is that all objects around us are also in orbits; if the gravitational attractions were not quite the same for the different objects, the objects would tend to have different orbits and there would be effects associated with this difference. The net effect would be like that of a small force in the direction of the sun. Such an effect has been looked for, in terms of a diurnal oscillation; comparing the behavior of a pair of weights on a torsion balance at dawn and at dusk, for example. Naturally, there are differences measured, some due to the fact that different sides of the building are at different temperatures— the difficulty in many of these experiments with very small effects lies in making sure that one is indeed measuring what one thinks, rather than something else. Nevertheless, the conclusion from the results is that all objects are as well balanced in their orbits as the earth is, at least to an accuracy of one part in 10⁸. This accuracy of one part in 10⁸ is already telling us many important things; for example, the binding energy of nuclei is typically of the order of 6 MeV per nucleon, and the nucleon mass is like 940 MeV; in short the binding energy is of the order of one percent of the total energy. Now, an accuracy of 10⁸ tells us that the ratio of the inertial and gravitational mass of the binding energy is constant to within 1 part in 10⁶. We even have a check on the ratio of the electronic binding energies for electrons in the lower shells, since 10⁻⁸ of a nucleon mass is something like 9 electron volts. If the experiment can be pushed to an accuracy of one in 10¹⁰, as it may be in the near future, we would have a five percent check on the ratio for even chemical binding energies, which are of the order of two volts.

At these accuracies we also have a check on the gravitational behavior of antimatter. The striking similarity of electrical and gravitational forces in their inverse-square behavior, has made some people conclude that it would be nice if antimatter repelled matter; they say: in electricity, likes repel, and opposites attract; it would be nice if in gravitation it were the other way around, with likes attracting and unlikes repelling; the only candidate for gravitational “unlike” is antimatter. But with an accuracy of one in 10⁸ we can check on the gravitational behavior of corrections to electronic binding energies of the K-electrons in lead due to the vacuum polarization, which involve virtual pairs and thus antimatter. It may be said at this point that there is absolutely no evidence that would require us to assume that matter and antimatter differ in their gravitational behavior. All the evidence, experimental and even a little theoretical, seems to indicate that it is the energy content which is involved in gravitation, and therefore, since matter and antimatter both represent positive energies, gravitation makes no distinction.

Further evidence comes from the fact that light “falls” in a gravitational field by an amount which is given by our theory; it is deflected as it goes by the sun, for example, by a measurable amount, which we shall calculate later. But the photon is its own antiparticle, so that we must conclude that both particle and antiparticle in this case show identical gravitational behavior. It might be amusing as an exercise to some people to construct a theory in which photons that came from an electron were different from photons that came from a positron, but since there is absolutely no evidence that such a thing is necessary to explain any phenomena, there is very little point in trying to construct such a theory; it would have to explain all known things as well as the present theory— and it is most likely that it could be proved wrong by some other effect, in that it would possibly predict some new electrodynamic effects which experiment would quickly show absent.

The most direct evidence that matter and antimatter do behave identically with regard to gravitation comes from the experiments on the decay of the K₀ and ${\overline{K}}_0$ done at M.I.T. The experiment itself is not without its flaws, but perhaps we may use the results to kill the theory of unequal behavior. These arguments are due to M. Good [Good 61].

We suppose that the K₀ and ${\overline{K}}_0$ are affected by gravity, otherwise the argument does not work. These two are antiparticles of each other, so we will see what happens if one is attracted, and the other is repelled by gravity. These particles have two decay modes which are describable as

$K_1=\frac{1}{\sqrt{2}}(K_0+{\overline{K}}_0),K_2=\frac{1}{\sqrt{2}}(K_0+{\overline{K}}_0).$

The amplitudes for decay by these two modes interfere; the experiment has detected this interference, and assigned a value Δm to the mass difference, such that $\text{Δ}m<\hslash /{10}^{-10}$ sec. This value is inconsistent with the idea that matter is attracted but antimatter repelled, because of the fact that the experiment was carried out in the gravitational field of the earth; if the gravitational potential is ϕ, then there is an increase or decrease in mass by mϕ for one, and −mϕ for the other; the expected mass difference is larger than the limit set by the M.I.T. experiment. If we consider not the earth’s gravitational potential, but the sun’s, which is larger, or even the Galaxy’s, we get better and better limits on the degree to which the equality of gravitational interaction holds. The whole argument can be brushed aside by those who cling to the antimatter-repels theory; all that is needed is that K₀ and ${\overline{K}}_0$ should not be gravitating particles, but this requires a new special assumption. It is evident that any single experimental fact can be disregarded if we are willing to think up a special reason why the experiment should show the result that it does.

It is also known that single free neutrons fall in a gravitational field as might be expected. This is known to fair accuracy because it must be taken into account in designing neutron interferometers; slow neutrons from a pile may be collimated into narrow beams, and detected some distance away, of the order of hundreds of feet; it is found that they fall in the earth’s gravitational field like any other particles we can measure. In summary, the first amazing fact about gravitation is that the ratio of inertial mass to gravitational mass is constant wherever we have checked it.

The second amazing thing about gravitation is how weak it is. It is in fact so weak that if the Venutians had called the β-decay interactions the “Weak” interactions, the discovery of gravitation would be a tremendous embarrassment. Evidently, gravitation...