2⁵ Problems for STEM Education

Valery Ochkov

• Publisher: Chapman and Hall/CRC
• Year: 2020
• Print ISBN: 9780367345259
• eBook ISBN: 9781000762907
• Topic: Computer Science
• Subtopic: Computer Science General
• Index: Computer Science

25 Problems for STEM Education introduces a new and emerging course for undergraduate STEM programs called Physical-Mathematical Informatics. This course corresponds with the new direction in education called STE(A)M (Science, Technology, Engineering, [Art] and Mathematics). The book focuses on undergraduate university students (and high school students), as well as the teachers of mathematics, physics, chemistry and other disciplines such as the humanities. This book is suitable for readers who have a basic understanding of mathematics and math software.

Features

• Contains 32 interesting problems (studies) and new and unique methods of solving these physical and mathematical problems using a computer as well as new methods of teaching mathematics and physics
• Suitable for students in advanced high school courses and undergraduates, as well as for students studying Mathematical Education at the Master's or PhD level
• One of the only books that attempts to bring together ST(E)AM techniques, computational mathematics and informatics in a single, unified format

STUDY 1

Formulas for Calculations
Or

Chekhov’s Gun

Abstract

Mathematical expressions can be added or edited in electronic media as embedded calculations. Formulas in an electronic document are not just expressions written in a formal language, they are also an object that could be studied, helping to comprehend a text and avoid many typos and mistakes typical of mathematical formulas found in print. This Study describes some features of formulas embedded in online scientific literature and educational web apps. The Study is based on the experience of teaching engineering subjects and math assisted by the visualization of calculations. The author examines key features and practical application of calculations and formulas embedded into the scientific and educational texts.

Mathematics: Formulas.

Physics: Units, empirical and pseudo-empirical formulas, molarity, molality.

IT: Cloud calculation, modern publishing process.

Art: Anton Chekhov.

Study website: https://community.ptc.com/t5/PTC-Mathcad-Questions/PhysMathStudy1/m-p/85566.

A lot of changes are taking place in the educational and scientific content publishing arena. Traditional print is enhanced and often supplanted by electronic materials with embedded features such as web links, bookmarks, comments, references to forums, and video clips or animations [1].

Embedded calculations play an important role among these features, enhancing comprehension of the math while enabling live computation [2].

There is a wide variety of software capable of supporting embedded calculations. For example, the symbolic math engine Maple has found wide use in academia for differentiation and integration. The popular programming language Python is used for realization of algorithms in TeX documents [3]. Math formulas on HTML pages can be supported by Mathcad [4]. Cloud computing applications are also becoming more widespread [5].

Regardless of the technology used, a modern electronic textbook is not just a web-enabled text. It is also a self-contained learning tool [6]. It helps us to comprehend math better, allows for calculation and visualization of solutions in the form of graphs, and can be used for in-text exercises.

If there is an equation in a book, the reader should be able to use it for calculation right there. Additionally, readers should be able to change the variables in the equation. This also applies to tables and graphs containing functional dependencies [7].

The following are some observations from our pedagogical practice that illustrate the usefulness of embedded equations in education.

1. 1. In a physics department, students can conduct lab experiments and then use a computer to access a web page with live calculations, to enter data points and to fit a curve using the least-squares method. This method used to be the normal approach. Now, an increasing number of students use smartphones and tablets. When asked why they do not use the lab computer, students often reply: “I hardly know how to work with a standard keyboard, and I can input data faster on the tablet.”
2. 2. During math, physics and chemistry classes, students often use their mobile devices (smartphones, tablets, notebooks) to go to a math website and to key in an algebraic or differential equation (see Figure 1.2) in order to find an analytic or numeric solution that validates calculations written by the lecturer on the blackboard.
3. 3. Finally, during a physics class, a student might derive an equation describing string vibration and then create an animation for its visualization.

There is a new trend in the content and in the production of scientific papers, handbooks, monographs and textbooks containing calculations. In the old days, authors submitted their work to publishers in the form of typed manuscripts with handwritten formulas and special characters. Now, publishers require electronic files with the text in MS Word and formulas created in a math editor or native software; the formulas are scanned and inserted as images into the text.

Formulas in scientific papers and textbooks are there for the purposes of calculation. In electronic formats, they can be used for computing right on the screen. Printed formulas can be easily validated by using an interactive electronic version. This is a revolutionary change!

The production of electronic handbooks with embedded interactive equations is described in [8]. Making equations interactive reveals many typographical and other errors in the formulas. For example, multiple errors were found during the development of a series of web-based handbooks called “Heat Technology and Power Engineering” and corrected for the subsequent edition.

During peer review of scientific papers, we are often asked by editors to validate numeric solutions. While the damage caused by typos in regular text is negligible, those in formulas can lead to serious consequences. For example, during the review of an article on the thermal conductivity of an aqueous solution of NaCl, calculations were validated using the Mathcad Calculation Server. This revealed that some equations and coefficients in the article had typos. When these were corrected the article was published free of error and with a reference to “live” computing.

In this chapter of the book, we will examine various aspects of computing with embedded formulas and discuss ways of improving the quality and precision of solutions by using validated formulas.

Modern calculation apps such as Mathcad can handle units of measurement. This is very convenient due to the automatic conversion of input and output values with different units, and the control over their dimensional compatibility. However, there are some issues.

There are two types of scientific equations—physical and empirical. The former deal with physical values and can be used with any appropriate units of measurement. Good examples of these formulas are E = m·c² and F = m·a. Calculation apps will solve these equations correctly regardless of the units as long as they have the right dimension, and they will indicate an error when the dimensions are not compatible. Empirical equations, created as a rule by statistical treatment of experimental (empirical) data, require numeric input in the stated units of measurement. Probably the simplest and best known empirical formula is that linking the height of an average man with his weight [4]: height of a person in centimeters is his weight in kilograms plus 100. This formula, written in Mathcad, and the units of measurement are shown in Figure 1.1. The results in Figure 1.1 are rounded, although variables in equations contain 15 digits in the mantissa. This detail is an important aspect of the creation of “live” equations. In paper handbooks, monographs and textbooks, calculation of the systems of equations is done by rounding intermediate results and then using these results in other equations. In computer calculations, variables retain maximum precision. The results of these calculations would thus be slightly different from those in paper publications.

FIGURE 1.1 Input of a simple empirical equation.

FIGURE 1.2 Working with pseudo-empirical formulas.

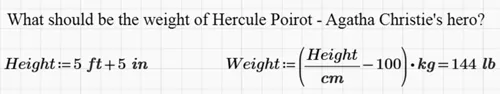
In handbooks, the basic units of measurement are shown in the legends for physical formulas. However, machine computing of these formulas is done without using the units. Here is a simple example: F = m·a, where F is force in N (newton), a is acceleration in m/s², and m is mass in kg. For modern calculation applications input of the units is redundant because all appropriate conversions for the derived units are done automatically.

We should not forget about physical problems with solutions that contain numbers beyond the range of computer calculations. They could have both very large and very small parameters, resulting in incorrect rounding due to simultaneous processing of large and small numbers. Also, solution algorithms for math models could become unsuitable if model equations contain variables that differ by several orders of magnitude. In this case, the errors for the large parameters could be on the same scale as the parameters themselves and could significantly distort the values for the small parameters. Before solving these equations, it is advisable to modify them to reduce the spread between the magnitudes of parameters and to reduce the number of arithmetic operations leading to an accumulation of errors.

A solution is to replace the variables with dimensionless quantities prior to calculation, making all variables in a math model practically the same magnitude. As a rule,...

Table of contents

• Cover
• Half-Title
• Title
• Copyright
• Contents
• Acknowledgements
• Author
• INTRODUCTION
• STUDY 1  ▪  Formulas for Calculations Or: Chekhov’s Gun
• STUDY 2  ▪  Swan, Crayfish and Pike Or: Scalar and Vector in Computer Calculations
• STUDY 3  ▪  The Gold-Bug Or: Roman-Arab Cryptography
• STUDY 4  ▪  Solvers Or: The Mathcad Magnificent Seven
• STUDY 5  ▪  Guess the Image Or: The Matrix Game
• STUDY 6  ▪  How Much Or: The Old Problem in a New Way
• STUDY 7  ▪  Catenary Or: The Fifth Element
• STUDY 8  ▪  Live Kinematic Schemes Or: Arm of Hella
• STUDY 9  ▪  Celestial Mechanics Or: Kepler’s Watch
• STUDY 10  ▪  Recursion Or: A Knight’s Tour
• STUDY 11  ▪  Yes–No in Mathcad Or: Boole’s Origami
• STUDY 12  ▪  Fuzzy Sets Or: Optimal Fire Bucket
• STUDY 13  ▪  The Journey of a Circle in a Triangle, and of a Triangle in a Hollow Or: A Self-Directed Computer Director
• STUDY 14  ▪  Interpolation, Extrapolation and Fitting Or: Lies, Damned Lies and Statistics
• STUDY 15  ▪  Go There, Knowing Where to Go Or: New Swiss Watches
• STUDY 16  ▪  Heads or Tails Or: A Three-Way Duel in Monte Carlo
• STUDY 17  ▪  Geese Are Flying Or: The Problem of Fishermen and Fish
• STUDY 18  ▪  Alphabetical Puzzle Or: Help Yourself So That the Computer Helps You!
• STUDY 19  ▪  Seven Computational Curves Or: Apollonius Bicycle and Apollo Guitar
• STUDY 20  ▪  Journey from Home to School on the Fermat Route Or: The Second Optical Property of Hyperbola
• STUDY 21  ▪  Optimization of Potential Energy Or: Curves of the Second-Order in Statistics
• STUDY 22  ▪  Parallel Computing Or: Put Yourself in Order!
• STUDY 23  ▪  How to Calculate a Ship Or: How You Name a Boat Is How it Will Sail
• STUDY 24  ▪  How to Calculate a Rocket Or: “… and on Mars Will Blossom Apple Trees”
• STUDY 25  ▪  Hybrid Calculations on the Computer Or: One More about a Cone
• STUDY 26  ▪  Funicular Polygons in Statics, Kinematics and Dynamics Or: Isaac Newton versus Joseph Louis Lagrange
• STUDY 27  ▪  BHL Or: Application for the Ig Nobel Prize
• STUDY 28  ▪  Tomography = IT + Mathematics + Physics + Biology Or: Worker-Peasant Graphics
• STUDY 29  ▪  A New Ellipse Or: Math Porcelain Service
• STUDY 30  ▪  What Lies behind a Simplified Formula Or: Hybrid Calculation of the Otto Cycle
• STUDY 31  ▪  Mad Chain Or: Physical and Mathematical Informatics
• STUDY 32  ▪  STEM Education And Or: Science Fiction
• INDEX