Unlocking Mathematics Teaching

Valsa Koshy, Jean Murray

• Publisher: Routledge
• Year: 2011
• Print ISBN: 9780415579292
• eBook ISBN: 9781136808500
• Topic: Education
• Subtopic: Education General

Now in a fully updated second edition, Unlocking Mathematics Teaching is a comprehensive guide to teaching mathematics in the primary school. Combining theory and practice, selected experts outline the current context of mathematics education. They suggest strategies, activities and examples to help develop readers understanding and confidence in delivering the curriculum. The book combines an accessible blend of subject knowledge and pedagogy, and its key features include:

• Advice on teaching mathematics to high and low attainers;
• Guidance on teaching mental maths;
• Ideas for incorporating ICT;
• Guidance on assessment in mathematics education;
• Teaching problem solving;
• Numerical and non-numerical examples;
• Updated references, taking into account the Williams Report.

This book will be of interest to all primary education students and practising teachers looking to increase their confidence and effectiveness in delivering the mathematics curriculum.

1
		Aspects of numeracy Bob Jeffery

Introduction

Behind the apparently straightforward attributes of numeracy lie some rather puzzling features connected with both fundamental aspects of number and the complex historical background of present-day approaches. This chapter aims to set a context for the rest of the book by highlighting some of these aspects through a series of interactive exercises.

Numeracy comprises the knowledge, skills and understanding necessary to move around in the world of numbers with confidence and competence.

The term ‘confidence’ as used here implies a feeling of security, the ability to make connections between the various aspects of numeracy and the courage to develop personal methods and vary them according to the particular problem. ‘Making connections’ is used rather than ‘understanding’ as the latter term has a history of abuse in the teaching of mathematics as in ‘Do you understand what I want you to do?’ Many adults express quite the opposite of confidence about numeracy.

The chapter does not provide a comprehensive treatment, but the exercises are designed to help the reader build some connections between different strands and to develop a personal story about numeracy. In this respect, it is in line with the definition above. You do not become numerate without thinking for yourself and you cannot help others without some appreciation of potential difficulties.

The exercises require you to engage in mathematical thinking and to reflect on your own thoughts and experience. There is a commentary at the end of the chapter. To get the maximum benefit carry out the exercises before reading the commentary.

Exercise 1: What is number?

Number is an abstract concept.

It is unfortunate that the term ‘abstract’ has become almost a term of abuse in the English language. However, mathematics is a subject that deals with abstract concepts and children work with abstract ideas in their earliest mathematical encounters. Suppose you have just arrived from another planet and you have no concept of number. You enter a world where everyone is talking about number using number names such as one, two, three …. What are the possible sources of confusion as you try to understand what is going on? You could start by thinking of someone pointing at a picture of three yellow ducks and saying ‘three’. As far as you are concerned the word might mean birds, yellow, dinner or three! How can you learn what is meant by ‘three’? See also the example in Figure 1.1.

Figure 1.1 Does ‘Erh’ mean ‘two’, ‘red’ or ‘telephone box’ in Chinese?

Exercise 2: Mathematics in the mind

Try the problem shown in Box 1.1.

Box 1.1 Breaking sticks

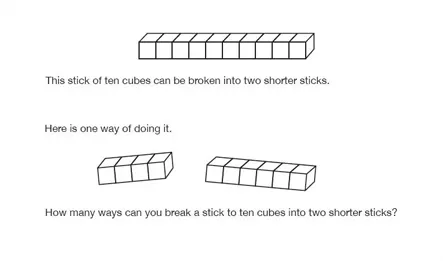
There are two different answers that are commonly given. What are they? Check with someone else if you can see only one answer. What is going on here and what has it got to do with the abstract? Did you stick with the physical problem or start playing with numbers?

Postscript

The picture shows the stick broken into six cubes and four cubes. The difference between six and four is two. Take a ten-stick and break it so that the difference is six. Try to do the same for differences four, eight and three. Make up a general rule about this activity. Note to what extent you rely on manipulating the cubes (perhaps in times of stress!) and what kind of thought experiments you make. Watching children do these activities will tell you quite a lot about their numeracy.

Exercise 3: Counting

Look at the exercise shown in Figure 1.2. For this exercise to be effective you must count the squares in each box. Review your strategies and difficulties. You may find it useful to use terms such as ‘one-to-one correspondence’, ‘order’, ‘pattern’, ‘grouping’, ‘counting in …’, ‘odd and even’.

Figure 1.2 Counting.

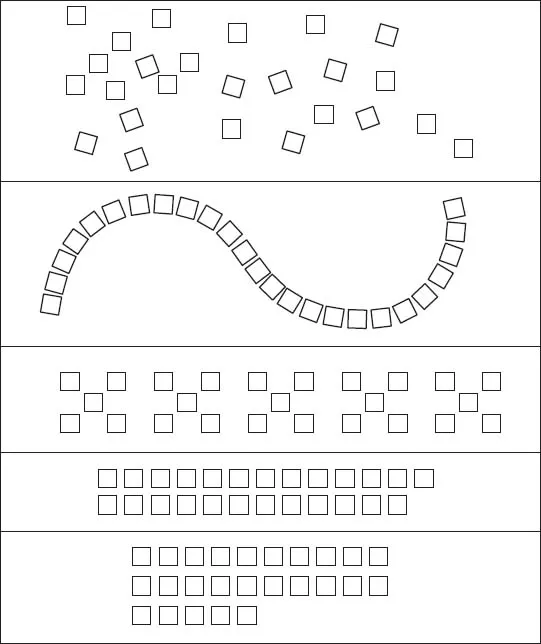
Exercise 4: Fundamental ideas about number and number
operations (Box 1.2)

Box 1.2 Number and number operations

Sit down with at least one friend and a box of mixed materials – any small objects that can be used for counting. It would be useful to have materials that possess a number of different attributes such as different colour or shape.Try to use the materials to illustrate as many of these terms as possible.

• ordinal number, cardinal number;
• counting;
• one-to-one correspondence;
• counting on and counting back;
• symbolism and numerals;
• repeated addition;
• repeated subtraction;
• sharing;
• addition, subtraction, multiplication, division;
• odd and even;
• more than, fewer than;
• grouping;
• place value;
• the difference.

Exercise 5: Mental arithmetic: an investigation

For the activity in Box 1.3 you will need at least one friend to help. The calculations should all be done mentally. There is no limit on time!

Do them one at a time and then compare notes about your methods after each one. Take your time to explore the differences fully, including the origins of your methodology, speed and accuracy, relationships with written calculations, mental images and personal feelings.

Box 1.3 Mental arithmetic

• Add 18 and 14
• From 125 subtract 88
• 26 multiplied by 9
• 105 divided by 13
• From 152 subtract 63
• 48 multiplied by 12
• 132 divided by 4

Exercise 6: With and without place value

Life is made easier by having a place value system of numeration, both for naming numbers and calculations (Box 1.4). The Romans didn’t crack this one!

Box 1.4 Place value

A Roman nightmare

24 + 19 = 14 + 15 = 36 – 19 =

Convert these to Roman numerals, try the calculations and weep! The Hindu–Arabic system of numeration that we use offers some advantages. What are they? Discuss.

ENGLISH	CHINESE
One	E
Two	Erh
Three	San
Four	Ssu
Five	Wu
Six	Liu
Seven	Chi
Eight	Pa
Nine	Chiu
Ten	Shih
Twenty	Erh Shih
Fifteen	Shih Wu
Forty-five	Ssu Shih Wu
Fifty-one	Wu Shih E
Seventy-eight	Chi Shih Pa

What is 32 in Chinese? What is 89? How did you do it? The number of numbers is infinite, so how is it that we can have a name for every number? Investigate counting in some other languages. How much do you need to learn in order to count to 1000?

Exercise 7: Modelling number: place value 1

This commercially produced material (Box 1.5) is attributed to Z. P. Dienes and has its uses in helping to resolve problems about the nature and role of the place value system of numeration. Try...

Table of contents

• Cover
• Title
• Copyright
• Contents
• List of illustrations
• Notes on contributors
• Acknowledgements
• Introduction
• 1. Aspects of numeracy
• 2. Using and applying mathematics in Key Stage 2
• 3. Learning effective strategies for mental calculation
• 4. Talking about real-life mathematics
• 5. Developing problem-solving skills in mathematics
• 6. Numeracy and low attaining children
• 7. Teaching mathematically promising children
• 8. Assessing mathematical learning
• Index