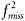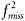Statistical and Methodological Myths and Urban Legends

Doctrine, Verity and Fable in Organizational and Social Sciences

Charles E. Lance, Charles E Lance, Robert J Vandenberg

• Publisher: Routledge
• Year: 2010
• Print ISBN: 9780805862379
• eBook ISBN: 9781135269654
• Topic: Psychology
• Subtopic: History & Theory in Psychology
• Index: Psychology

This book provides an up-to-date review of commonly undertaken methodological and statistical practices that are sustained, in part, upon sound rationale and justification and, in part, upon unfounded lore. Some examples of these "methodological urban legends", as we refer to them in this book, are characterized by manuscript critiques such as: (a) "your self-report measures suffer from common method bias"; (b) "your item-to-subject ratios are too low"; (c) "you can't generalize these findings to the real world"; or (d) "your effect sizes are too low".

Historically, there is a kernel of truth to most of these legends, but in many cases that truth has been long forgotten, ignored or embellished beyond recognition. This book examines several such legends. Each chapter is organized to address: (a) what the legend is that "we (almost) all know to be true"; (b) what the "kernel of truth" is to each legend; (c) what the myths are that have developed around this kernel of truth; and (d) what the state of the practice should be. This book meets an important need for the accumulation and integration of these methodological and statistical practices.

Part 1
Statistical Issues

1
Missing Data Techniques and Low Response Rates

The Role of Systematic Nonresponse Parameters

Daniel A. Newman

This chapter attempts to debunk two popular misconceptions (or legends) about missing data: Legend #1, low response rates will necessarily invalidate study results; and Legend #2, listwise and pairwise deletion are adequate default techniques, compared with state-of-theart (maximum likelihood) missing data techniques. After reviewing general missingness mechanisms (i.e., MCAR, MAR, MNAR), the relevance of response rates and missing data techniques is shown to depend critically on the magnitude of two systematic nonresponse parameters (or SNPs: labeled d_miss and

). Response rates impact external validity only when these SNPs are large. Listwise and pairwise deletions are appropriate only when these SNPs are very small. I emphasize (a) the need to explicitly identify and empirically estimate SNPs, (b) the connection of SNPs to the theoretical model (and specific constructs) being studied, (c) the use of SNPs in sensitivity analysis to determine bias due to response rates, and (d) the use of SNPs to establish inferiority of listwise and pairwise deletion to maximum likelihood and multiple imputation approaches. Finally, key applications of missing data techniques are discussed, including longitudinal modeling, within-group agreement estimation, meta-analytic corrections, social network analysis, and moderated regression.

Organization of the Chapter

The material that follows is organized into six sections. First, I distinguish three levels of missing data (item level, scale level, and survey level), two problems caused by missing data (bias and low statistical power), and three mechanisms of missing data (MCAR, MAR, and MNAR). Second, I present a fundamental principle of missing data analysis (“use all the available information”) and review four missing data techniques (listwise deletion, pairwise deletion, maximum likelihood, and multiple imputation) in light of this fundamental principle. Third, I introduce two systematic nonresponse parameters (SNPs: d_miss and

) and illustrate how response rate bias depends entirely on the interaction between SNPs and response rates, rather than on response rates alone. Fourth, I present a theoretical model of survey nonresponse, highlighting how SNPs and response rate bias vary with the substantive constructs being studied. Fifth, I use the aforementioned information to redress two popular legends about missing data. Sixth, I review several prominent data-analytic scenarios for which the choice of missing data technique is likely to make a big difference in one’s results.

Levels, Problems, and Mechanisms of Missing Data

Missing data is defined herein as a statistical difficulty (i.e., a partially incomplete data matrix) resulting from the decision by one or more sampled individuals to not respond to a survey or survey item. The term survey nonresponse refers to the same phenomenon, at the level of the individual nonrespondent. Missing data is a problem from the perspective of the data analyst, whereas survey nonresponse is an individual decision made by the potential survey participant. Although nonresponse decisions may vary in how intentional they are (e.g., forgetting about the survey vs. discarding the survey deliberately), the above definition of survey nonresponse assumes that a potential respondent saw the survey invitation and made a de facto choice whether to complete the measures.

Three Levels of Missing Data

The missing data concept subsumes three levels of nonresponse: (a) item-level nonresponse (i.e., leaving a few items blank), (b) scale-level nonresponse (i.e., omitting answers for an entire scale or entire construct), and (c) unit- or survey-level nonresponse (i.e., failure by an individual to return the entire survey). The response rate, which is a ratio of the total number of completed surveys to the number of solicited surveys, is an aggregate index of survey-level nonresponse.

Two Problems Caused by Missing Data (External Validity and Statistical Power)

There are two primary problems that can be caused by low response rates. The first problem is poor external validity (i.e., response rate bias), which in this case means that the results obtained from a subsample of individuals who filled out the survey may not be identical to results that would have been obtained under 100% response rates. In other words, a respondents-based estimate (e.g., respondentsbased correlation: r_resp) can sometimes be a biased (over- or underestimated) representation of the complete-data estimate (e.g., complete-data correlation: r_complete).

The second problem caused by missing data is low statistical power, which means that—even when there is a true nonzero effect in the population—the sample of respondents is too small to yield a statistically significant result (i.e., Type II error of inference). I clarify that power is a function of the sample size, and not a direct function of response rate. For example, attempting to sample 1,000 employees and getting a 15% response rate yields more statistical power (N = 150) than attempting to sample 200 employees and getting a 60% response (N = 120). After controlling for sample size, response rates have negligible effects on power.

Missingness Mechanisms (MCAR, MAR, and MNAR)

Data can be missing randomly or systematically (nonrandomly). Rubin (1976) developed a typology that has been used to describe three, distinct missing data mechanisms (see Little & Rubin, 1987):

MCAR (missing completely at random)—the probability that a variable value is missing does not depend on the observed data values or on the missing data values. The missingness pattern results from a completely random process, such as flipping a coin or rolling a die.

MAR (missing at random)—the probability that a variable value is missing partly depends on other data that are observed in the data set but does not depend on any of the values that are missing.

MNAR (missing not at random)—the probability that a variable value is missing depends on the missing data values themselves.

Of the three missingness mechanisms, only MCAR would be considered “random” in the usual sense, whereas MAR and MNAR would be considered “systematic” missingness (note the unusual label, missing at random [MAR], to describe a particular type of systematic missingness). For a helpful example of the MAR and MNAR mechanisms, consider two variables X and Y, where some of the data on variable Y are missing (Schafer & Graham, 2002). Missing data would be MAR if the probability of missingness on Y is related to the observed values of X but unrelated to the values of Y after X is controlled (i.e., one can predict whether Y is missing based on the observed values of X). The data would be MNAR if the probability of missingness on Y is related to the values of Y itself (i.e., related to the missing values of Y). Note that in practice, it is usually considered impossible to determine whether missing data are MNAR, because this would require a comparison of the observed Y values to the missing Y values, and the researcher does not have access to the missing Y values.

Why do missing data mechanisms matter? Missing data mechanisms determine the nature and magnitude of missing data bias and imprecision (see Table 1.1). In general, systematic missingness will lead to greater bias in parameter estimates (e.g., correlations and regression weights) than will completely random missingness. That is, MCAR is harmless in that it does not bias the means, standard deviations, and estimated relationships between variables. Systematic missingness (MAR or MNAR), on the other hand, will often bias parameter estimates.

Table 1.1 Parameter bias and Statistical Power Problems of Common Missing Data Techniques

Missing Data Treatments

A Fundamental Principle of Missing Data Analysis

Across missing data conditions, the best data-analytic methods for dealing with missing data follow a simple yet fundamental principle: use all of the available data. This principle characterizes all of the recommended missing data techniques shown in Table 1.2. However, the principle is not found in many of the more commonly applied missing data techniques, such as listwise and pairwise deletion.

In general, item-level nonresponse can be redressed through mean_item imputation (Roth, Switzer, & Switzer, 1999), meaning that a researcher can average across the subset of scale items with available responses to calculate a scale score. This approach works especially well when scale items are essentially parallel. Unfortunately, there is a relatively common practice of setting an arbitrary threshold number of items that must be completed in order to calculate a scale score (e.g., if 4 or more items from an 8-item scale are complete, then those items can be averaged into a scale score; otherwise, set the respondent’s scale score to “missing”). Setting such an arbitrary threshold violates the fundamental principle of missing data analysis, because it throws away real data from the few items that were completed. Dropping an entire scale from analysis simply because some of its items were omitted will typically produce worse biases, in comparison

Table 1.2 Three levels of Missing Data and Their Corresponding Missing Data Techniques

to assuming that the few completed items appropriately reflect the scale score.

Next, scale-level nonresponse can be treated through maximum likelihood or multiple imputation techniques (ML and MI techniques; Dempster, Laird, & Rubin, 1977; Enders, 2001; Schafer, 1997), in which a researcher estimates the parameters of interest (e.g., correlations, regression weights) using a likelihood function (or alternatively using a Bayesian sampling distribution) based on observed data from all of the measured variables. (ML and MI will be discussed in more detai...

Table of contents

• Contents
• Preface
• About the Editors
• Acknowledgments
• Introduction
• Part 1 Statistical Issues
• Part 2 Methodological Issues
• Subject Index
• Author Index