Crocheting Adventures with Hyperbolic Planes

Tactile Mathematics, Art and Craft for all to Explore, Second Edition

Daina Taimina

• Publisher: CRC Press
• Year: 2018
• ISBN:
  9781351402194
• Edition: 2
• Topic: Mathematics
• Subtopic: Mathematics General
• Index: Mathematics

Winner, Euler Book Prize, awarded by the Mathematical Association of America. With over 200 full color photographs, this non-traditional, tactile introduction to non-Euclidean geometries also covers early development of geometry and connections between geometry, art, nature, and sciences. For the crafter or would-be crafter, there are detailed instructions for how to crochet various geometric models and how to use them in explorations. New to the 2nd Edition; Daina Taimina discusses her own adventures with the hyperbolic planes as well as the experiences of some of her readers. Includes recent applications of hyperbolic geometry such as medicine, architecture, fashion & quantum computing.

Chapter 1

What Is the Hyperbolic Plane? Can We Crochet It?

Positive and Negative Curvature

When we talk about numbers, we can divide them into positive numbers, negative numbers, and zero.

Elevator buttons in France: the ground floor is numbered 0

When we scribble different lines with a pencil on a piece of paper, we can get different shapes in the plane. The ones that are most useful in geometry are the ones that are “the same everywhere.” In the plane, such shapes are straight lines and circles. A straight line is called straight because it is not curved—in other words, we can say it has zero curvature. Circles are curved everywhere in the same way—so they have constant curvature.

Straight lines and circles are different from other scribbles because they are the same everywhere.

The larger the radius of a circle, the less curved it is. For example, if you look at part of a circle with a very large radius, the line will seem straight. Mathematicians express this property by saying that circles with radius R have curvature 1/R. The notion of the curvature is used to study curves that are different from circles and straight lines. We can say that the curvature of a curve measures the failure of a curve to be a straight line. We know from school geometry that two circles are the same if they have the same radius. Using the notion of the curvature we can now say that two circles are the same if they have the same curvature.

For curves in a plane, the curvature can be negative (in a valley) or positive (on the top of a hill).

Imagine that we are sketching a landscape as children first learn to do, just with different curves; there can be hills and there can be valleys in this landscape. In our example, we are avoiding cliffs and sharp peaks or valleys. The skyline of the landscape is not uniformly curved everywhere, but at each point we can measure the curvature by the circle that would “best fit” in the curve at that point, as you can see in the picture. To distinguish numerically where the hills are and where the valleys are, we use a notion of one-dimensional positive and negative curvature. We can decide that hills have positive curvature where the circle would be inside the hill, below the ground; for valleys we say that the curvature is negative where the circle is above the ground. At some places positive curvature will turn into negative curvature, and at that place the curvature will be zero. It will be zero also everywhere that the curve is straight.

Can we make a similar distinction with surfaces?

Curvature is a mathematical notion widely used in differential geometry. What does it mean in simple words? If you look, for example, on the surface of your desk or on the floor in your room, you will notice that it is flat—there is no curvature, or we say that the curvature is zero. If you look at an orange or an egg, you will see that it is curved “outward”—we say that the curvature is positive. The egg is curved more at its tips and curved less in between and thus does not have constant positive curvature, but many oranges have almost constant positive curvature.

Two surfaces with positive curvature: on an egg it is varying, but on an orange, it is (almost) constant.

Now look at the surface of the pear. Most of its surface has positive curvature like an orange or an egg, but there are some points were the curvature is different. How can we describe this diff

Not all points on the pear have positive curvature.

Many leaves have interesting surfaces like in the picture with kale leaves.

Kale leaves have negative curvature.

In the early nineteenth century one of the greatest mathematicians of all times, Carl Friedrich Gauss (1777–1855), explored the idea that surfaces can be distinguished by their curvature at different points, which can be positive, negative, or zero. In the 1820s Gauss was a professional surveyor. This work inspired him to study the intrinsic geometry of surfaces. His concern was how one can determine the curvature of an arbitrary surface without knowing anything about how this surface might be embedded in space—in other words, asking whether and how one could determine the curvature of a surface through measurements made only along this surface, without knowing anything about the shape of this surface.

Consider an ant crawling on a big sphere, where the ant cannot see that it is on a sphere; how could this ant distinguish whether it is on a flat surface or on a curved surface? If the ant crawls on a straight line or on any other one-dimensional curve, it can move only in two directions: forward or backward. If the ant is on a two-dimensional surface, then it can choose to go backward or forward but also right or left. Still, the ant cannot see the surface it is on from the outside; it can explore the surface only intrinsically, not leaving this surface.

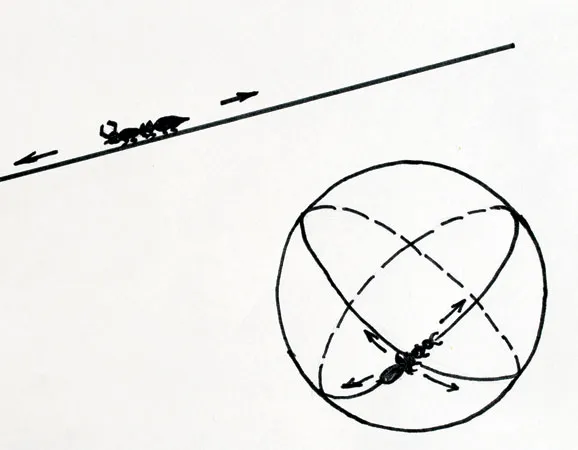
An ant on a curve can go in only two directions, but on a surface there are more choices.

Another great mathematician, Leonard Euler (1707–1783), had already introduced a notion of surface curvature, which was used in eighteenth-century calculus. But to use Euler’s method for surfaces, you had to know how the surface is embedded in space. This means that you had to be able to see the surface from another dimension. Gauss was able to prove that it is possible to find a way to determine the curvature of a surface that depends only on intrinsic properties of the surface.¹

If a surface has constant positive curvature, it will become closed, and it is called a sphere. Gauss used the radius of the sphere to determine the magnitude of the curvature. Every point on a sphere is the intersection of two great circles with the radius R. As defined earlier, the curvature of each of those circles is 1/R, so Gauss measured the curvature of a sphere as the product of the curvatures of these two great circles. Therefore, he defined the curvature of a sphere with radius R as the quantity 1/R²; so, as the radius, R, gets larger, the curvature, 1/R², gets smaller.

Spheres with different radii: the tennis ball has radius 3.5 cm and the metal ball has radius 0.5 cm.

Let us now look at a sketch of a three-dimensional landscape. There are hills, a pass, and the bowl-shaped bottom of the bay. We can draw two intersecting curves to define a point on the top of a hill and a point in the bay. Then, surface curvature at each of these points will be the product of curvatures of the two intersecting curves. Therefore, in both cases—on the top of a hill and in the bottom of the bay—we have positive curvature, since positive times positive equals positive and negative times negative equals positive. But at the pass, where there is one positive curve and one negative curve, the surface curvature will be negative. In general, we will define the curvature of the surface at a point in terms of the one-dimensional curvatures of two curves on the surface that intersect at that point.

Positive curvature is on the top of a hill (as a product of two positive curvatures) and in the lake (as a product of two negative curvatures), but on a pass the curvature is negative (as a product of positive and negative curvatures).

What Surface Will Have Constant Negative Curvature?

Cut from paper some regular hexagons. Try to put them next to each other. You can see that around each hexagon you can place six other hexagons, and then at each vertex there will be three hexagons and they will lay flat on the table. If you continue adding more hexagons, it looks like the surface o...