Mathematics: a Simple Tool for Geologists

Waltham, D., D. Waltham

• Publisher: Routledge
• Year: 2013
• Print ISBN: 9781032297590
• eBook ISBN: 9781134983087
• Topic: Physical Sciences
• Subtopic: Geography
• Index: Geography

Uses geological examples to illustrate mathematical ideas. Contains a large number of worked examples, and problems for students to attempt themselves. Answers to all the questions are given at the end of the book.

1Mathematics as a tool for solving geological problems

1.1 Introduction

This book is not about specialized geological mathematics. Mostly, this book is about simple mathematics, the sort that many people are introduced to at school. However, such mathematics is frequently poorly understood by geology undergraduates and few students are able to use the maths they know for solving realistic problems. The objectives of this book are to improve understanding of simple mathematics through the use of geological examples and to improve the ability to apply mathematics to geological problems.

This is not a formal mathematics textbook. My aim is to try to instil an intuitive feel for maths. I believe that this is more helpful than a rigid, formal treatment since formality can often obscure the underlying simplicity of the ideas.

Although this book concentrates upon standard mathematical procedures, it does contain a few more specialized techniques. The majority of the mathematics encountered by typical undergraduate students is therefore covered here. The exception is, perhaps, statistics which forms a large part of geo-mathematics and which is well covered by many excellent textbooks. The statistics chapter in this book should form a good introduction to the material covered in those more specialized texts.

Mathematics is much more akin to a language than a science. It is a method of communication rather than a body of knowledge. Thus, the best way to approach a book like this is as you would a text on, say, French or German. You are learning how to communicate with people who understand the mathematical language. You are not learning a collection of facts. Another similarity to learning a language is that you must never pass on to the next lesson until you have grasped the current one. If you do, you will get hopelessly lost and demoralized since succeeding chapters will simply make no sense.

So that you know you have understood sufficiently to move on, each chapter is sprinkled with examples for you to attempt. Mostly these are very short and simple. A few, however, are more difficult and are designed to make you think carefully about the maths just discussed. If you are unable to do one, you should read over the preceding paragraphs again and make sure that you have understood everything. If that does not help then get assistance. Each chapter concludes with additional simple questions as well as more wide-ranging questions which will test your ability to apply what you have learnt to more realistic problems. Outline answers to most questions are given at the end of the book and more complete answers are given for some of the more difficult problems. Look carefully at these complete answers since they also show how your answers should be set out. I assume, throughout this book, that you have a calculator and know how to use it.

One difficulty that many students have with mathematics is the large number of specialized mathematical words. Sometimes these words are completely new to the student whilst other times they are used in a similar, but somewhat more precise, manner to their everyday meaning. It is impossible to avoid use of such words since they are vital in mathematics. Wherever I introduce such a word it is in bold face (e.g. jargon).

This first chapter is about basic tools that are needed in succeeding chapters and will introduce you to the most important ideas needed for application of mathematical principles to geological problems.

1.2 Mathematics as an Approximation to Reality

Geology is frequently regarded as a qualitative (i.e. descriptive) science. Geological discussions often revolve around questions about what happened and in what order. For example, was a particular area under the sea when a given sedimentary rock was deposited and does the erosive surface at the top imply that uplift above sea level occurred subsequently? However, the same geological information can be described quantitatively (i.e. by numbers). In the preceding example, how deep was the sea and how long was it before uplift occurred? Geology is also concerned with the influence of one process upon another. How does changing water depth affect sediment type? Once again it is possible to do this quantitatively by producing equations relating, say, grain size to water depth (unlikely to be very accurate but in principle possible).

Figure 1.1 illustrates a situation in which a quantitative description can be attempted. The figure shows a lake within which sediment, suspended in the water, rains down and slowly builds up on the lake floor. Obviously early deposits will be covered by later ones. This results in a relationship between depth below lake bed and time since deposition; the deeper you go the older the sediments get. Now, if the rate at which sediments settle upon the floor is approximately constant, sediments buried 2 m below the lake bed are twice

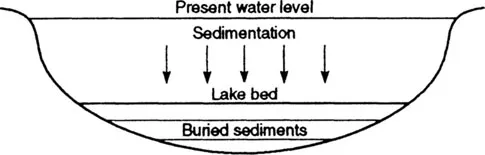
Figure 1.1 Sedimentation on a lake bottom. As sediment accumulates on the lake bed, older sediments are slowly buried by younger deposits.

as old as sediments buried by 1 m and sediments buried by 3 m are three times as old and so on. Thus, if you double depth, you double the age, if you triple depth you triple the age and so on. This means that the sediment age is proportional to burial depth. This can be expressed, mathematically, by the equation

where k is a constant. In other words, the age of the sediment equals its depth multiplied by a constant. Constants are values which do not change within a given problem. In the case of the problem above, the constant tells us how rapidly sediments accumulate. A large value for k implies that age increases very rapidly as depth increases (i.e. sediments accumulated very slowly). A low value implies that the age increases more slowly (i.e. sediments accumulated more rapidly). In a particular lake it might take 1500 years for each metre of sediment to accumulate. In this case k = 1500 years per metre (ym^-1). A lake with a lower sedimentation rate of, say, 3000ym^-1, would have a more rapid increase in age with depth of burial.

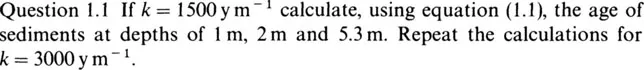
As you see, it is possible to produce mathematical expressions relating geological variables to each other (a variable is a quantity which, in a particular problem, can change its value, e.g. the v...

Table of contents

• Cover
• Title
• Copyright
• Contents
• Preface
• 1 Mathematics as a tool for solving geological problems
• 2 Common relationships between geological variables
• 3 Equations and how to manipulate them
• 4 More advanced equation manipulation
• 5 Trigonometry
• 6 More about graphs
• 7 Statistics
• 8 Differential calculus
• 9 Integration
• Appendix - Answers
• Index