Teaching Mathematics through Story

A creative approach for the early years

Caroline McGrath

• Publisher: Routledge
• Year: 2014
• ISBN:
  9781136598623
• Edition: 1
• Topic: Éducation
• Subtopic: Éducation générale

How do you make mathematics relevant and exciting to young children? How can mathematics and literacy be combined in a meaningful way? How can stories inspire the teaching and learning of mathematics?

This book explores the exciting ways in which story can be used as a flexible resource to facilitate children's mathematical thinking. It looks at the potential relationship between story and mathematics and practically demonstrates how they can be combined to help children connect, understand and express mathematical ideas using story language.

Written for all early years practitioners and students, the book offers a playful pedagogical approach to facilitating children's mathematical thinking which brings a creative satisfaction and confidence to teaching mathematics. Encouraging a creative approach to teaching mathematics that draws on picture books and oral mathematical stories, the book shows you how to:

• 
  
  

• Move from reading to telling stories with mathematical themes

• 
  
  

• Encourage children to pose and solve problems by playing with the plot of stories

• 
  
  

• Enable children to translate abstract mathematical ideas to concrete representations with supporting story props and puppets

• 
  
  

• Create original oral mathematical stories alongside children

• 
  
  

• Capture children's mathematical thinking in an observational framework, supported with audio or video recordings which can be shared with parents and colleagues

• 
  
  

• There are free audio recordings of children and adults telling oral mathematical stories, which feature in the book. These can be downloaded from: www.routledge.com/9780415688154

This book draws on practical work with children, educators, parents, professional storytellers, and trainee practitioners, who bring theoretical ideas to life and offer insight into their mathematical story experiences. It is a 'must have' for all those who want to make mathematics relevant, accessible and imaginative for young children.

1

Mathematics

Mathematics unfolds, like a flower opening, or a tree plunging roots deeper and crown higher.

(Hersh 1998, p.86)

This chapter aims to explore:

• problem posing and problem solving

• making mathematical generalisations

• an observational tool to conceptualise mathematics and capture children’s mathematical behaviour in play and as storytellers.

‘No Problem!’

‘One morning, Mouse was woken up by a heavy CLONK! outside her front door. Whatever’s that? Mouse thought. She nipped out of bed, opened the door and looked outside. In front of her was an ENORMOUS parcel. It was wrapped in brown paper and tied with string.

CONSTRUCTION KIT was stamped on the front and a pink card hung from the side. It read:

To Mouse,

Put together the things you see,

Then climb aboard and visit me!

Love from Rat.

“Oooooh!” squeaked Mouse.

She nibbled through the string, peeled off the paper and opened the parcel.

Inside was a mountain of bits and pieces – just waiting to be put together.

Mouse sniffed them and snuffled them.

She poked them and prodded them.

“I can put these together,” she said.

“NO problem.”

She was in such a hurry to begin that she forgot to look for the instructions.

She didn’t see the sheet of paper that said:

CONSTRUCTION KIT. HOW TO PUT IT TOGETHER!

Mouse set to work.

She joined pipes here and fixed wheels there.

She twisted and turned things.

She fiddled and twiddled things.

She bolted bolts and tightened nuts.’

Mouse makes something that looks like a bike but isn’t a bike. She calls it a ‘Bikeoodle-Doodle’ but didn’t get far before meeting Badger. Badger asks if there are any instructions and offers to fix it. Badger makes what looks like a car and calls it a ‘Jaloppy-Doppy’, which doesn’t work. Mouse and Badger meet Otter, who also asks if they have the instructions before offering to help and makes what looks like a boat; he calls it ‘a Boater-Roater’, which doesn’t work terribly well. They meet Shrew who finds the instructions, sets out all the pieces, follows the instructions and makes an aeroplane! They arrive at Rat’s house, who asks Mouse if she had any trouble putting the construction kit together: ‘No problem’ they say!

(Browne & Parkins 1993)

Figure 1.1 Aeroplane! (Browne & Parkins 1993). Text © 1993 Eileen Browne. Illustrations © David Parkins.
From ‘No Problem!’ by Eileen Browne, illustrated by David Parkins. Reproduced by permission of Walker Books Ltd, London SE11 5HJ, www.walker.co.uk

Introduction

The development of mathematical understanding involves building up connections in the mind of the child. Our aim is to help children make mathematical connections and build them into a coherent network (Haylock & Cockburn 2013; Suggate et al. 2010; 2006). Before exploring how story helps children to make mathematical connections, a variety of ideas about mathematics are explored.

Mathematics is difficult to conceptualise (Casey 2011; 1999) and a tool for observing children’s mathematical behaviour is shared to assist with seeing children’s play in a mathematical way. This tool can be used to record children, while listening to stories that have mathematical intentions, playing in a mathematical way or retelling mathematical stories. This observational tool is intended to document children’s mathematical behaviour in a way that can be readily interpreted, reflected on and shared with other adults and families of children observed (Carr 2001). The observational tool brings theoretical ideas about mathematics and children’s practical application of mathematics together and could be complemented with audio recordings of children at play or retelling mathematical stories. I suggest audio as this is less problematic than video in terms of ethical considerations, particularly for those not employed at the setting.

This observational tool is based on a mathematical perspective of Casey (2011; 1999) and principles concerning assessment that led Carr (2001) to the creation of the learning story format for assessment of learning. The intention is that the reader has a way of documenting children’s mathematical behaviour in play and as storytellers.

Problem posing and problem solving

We start with a story titled ‘No Problem!’ by Browne and Parkins (1993). ‘No Problem!’ reveals several trial and error attempts and a systematic strategy for problem solving: Mouse makes a ‘Bikeoodle-Doodle’; Badger makes a ‘Jaloppy-Doppy’; Otter makes a ‘Boater-Roater’; then we see the required systematic approach for solving this problem as Shrew follows instructions to make an aeroplane. Haylock and Cockburn describe how ‘[s]olving a problem may be a somewhat chaotic, backwards and forwards, roundabout, hit-and-miss, trial-and-error process, but presenting the solution requires the problem solver to organise his or her ideas into a coherent logical sequence’ (2013, p.302). As storytellers we model organising of ideas into a logical sequence when we tell a story.

Problem solving strategies

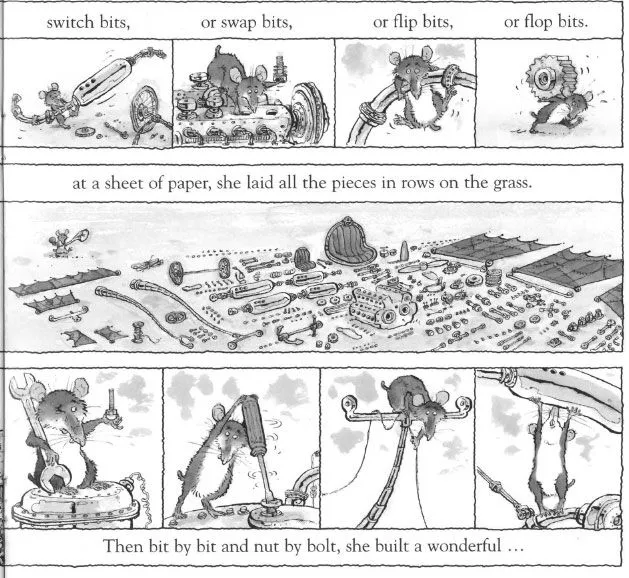
‘No Problem!’ expresses at least two different problem solving strategies: trial and error, and systematic thinking; both valuable mathematical strategies to solve prob lems. Strategies of trial and error produce results but a more systematic approach is required to solve the problem of constructing an aeroplane (Figure 1.2). Haylock and Cockburn (2013) encourage systematic ways of setting out information as this helps children to realise patterns. In order to take flight our stories need to be constructed in a sequential order.

Problem posing and solving connects story and mathematics

Problem posing and problem solving is central to both mathematics and story. Story characters are usually posed with problems that need to be solved. Often a story will have a mathematical idea in there somewhere. Relationships between story and mathematics can be problematised by changing something about the story or about the mathematics: what if Mouse, Badger and Otter do not meet Shrew? What if Shrew has not seen the instructions? A question such as ‘what if?’ poses a new problem, prompting story and mathematical thinking in order to find new solutions.

Figure 1.2 Shrew follows instructions and sets out parts to make the aeroplane (Browne & Parkins 1993).

Suggesting changes to a story plot potentially poses problems that require mathematical thinking: what if in the story about ‘Goldilocks and the Three Bears’ Goldilocks goes to the bears’ home with a friend? Or it is a family of four bears rather than three? By changing the idea of the story, we create new mathematical problems to think about: how will three bowls of porridge work with two imposters or four bowls of porridge with one?

Problem posing; problem solving; problem creating

The future mathematician should be a clever problem-solver: but to be a clever problem-solver is not enough.

Polya (1945, p.205)

Problem posing and solving are required when creating stories: a story is about a problem that needs to be solved. Creating a story requires thinking on a different level to that of retelling a familiar story. Children’s creation of stories is evident in play narratives, which we turn to in Chapter 3, and as storytellers, which we come to in Chapter 9.

Companions but different: the relationship between problem posing and problem solving

Mathematics is difficult to define. Hersh (1998, p.18) suggests that questions drive mathematics, and that ‘solving problems and making up new ones is the essence of mathematical life’. He describes how ‘mathematics is a vast network of interconnected problems and solutions’ (Hersh 1998, p.6). The subject is built up by individuals making connections and linking old ideas with new: ‘Mathematics is intensely interconnected and self-interactive. The new is vitally linked to the old. The old is revitalised, enriched, and complexified by interaction with the new’ (Hersh 1998, p.83). Mathematics is about problem posing, problem solving and making connections between ideas. Having identified problem posing and problem solving as being central to mathematics, we now consider how both differ but make necessary companions.

Problem posing

Among other things, problem posing pursues a particular thread of thinking: ‘What if we change something?’ Such a question opens a door to problem posing and extension of knowledge (McGrath, 2010). Children may well pose problems without conscious expression through words; adults can think of possibilities through such questions, or indeed intervene in a physical way; for example by moving an item beyond the reach of a crawling infant. It is worth noting how problem posing, like its companion problem solving, is a fundamental part of learning and doing mathematics (McGrath 2012a; 2012b). Problem posing is creating new problems from old ones, as well as making changes to given problems. What if one of the pieces of information in the problem is changed? Skilful questioning from this starting point leads to problem posing (McGrath 2010). Problem posing presents important thinking challenges. In story contexts we connect to this way of thinking, by playing with story plots we pose new problems.

What if?

If we change something about the story we change something about the mathematics and inversely, if we change something about the mathematics we change something about the story. The original relationship between story and mathematics is changed by asking ‘what if?’

Problem solving

Essentially, a problem presents a challenge (McGrath 2010). Problem solving challenges children to use what they already know. Different problems require different strategies to solve them (McGrath 2010). Some of the associated skills for solving problems are: estimating what a reasonable answer should be; recognising patterns; recording data; pictorially representing the problem and checking the answer for reasonableness.

Problem solving is using and applying acquired skills; problem posing is potentially extending knowledge. Therein lies the difference between the two; and problem posing brings possible risk, as we may not know the answer. Brown (2003, p.193) advocates that ‘the most effective way is to teach mathematics as a problem-posing-problem-solving cycle of activity’. Marion Walter in discussion with Baxter (2005) advises that ‘not all good problem solvers are good problem posers, and vice versa’. This brings us to another relevant point; creating problems for others to solve. In the context of story this could be changing the story in order to prompt new mathematical ideas.

Creating problems

Problem posing encourages curiosity, intellectual activity and sophisticated thinking. Creating problems for others to solve brings posing problems to a higher level; one must take a bird’s eye view and be aware of flaws inherent in the structure of the problem (McGrath 2010). This is high-level creative work. Combining the skills of problem solving and problem posing brings children on to creating problems. In the context of story: creating an original story is more challenging than retelling a familiar story or changing some feature of that story.

Polya (1945) advises us that being a problem solver is not enough: problem posing and creating involves thinking on a higher plane beyond applying what one already knows, which is problem solving. Hersh (1998) suggests questions are the driving force and that solving and making problems are at the heart of mathematics. Whereas problem solving is about applying acquired skills, problem posing is about changing something; it is a riskier business.

Creativity is a risky business

Problem posing is a r...