Becoming a Successful Teacher of Mathematics

Howard Tanner, Sonia Jones

• Publisher: Routledge
• Year: 2003
• Print ISBN: 9780415230681
• eBook ISBN: 9781134580897
• Topic: Education
• Subtopic: Education General

Becoming a Successful Teacher of Maths is a practical guide for newly qualified teachers of secondary mathematics. It develops the essential core knowledge, skills and understanding demanded by the new DfEE requirements for courses of initial teacher training. It is based on research findings relating to the organisation and management of maths classrooms, teaching approaches, assessment and the common misconceptions which often hinder pupils' progress in key areas of the National Curriculum. Theoretical principles are exemplified through case-study material. Suggestions for school-based activities are made. While being a practical 'how to' guide for beginning teachers, it also offers critical insights for more experienced teachers reflecting on their practice.

1: The National Curriculum A framework for teaching

INTRODUCTION

To teach mathematics in schools is a highly creative and complex endeavour. Mathematics is a body of knowledge which, although created by human beings, often seems to have a necessity of its own and to offer access to a truth which many claim to be real and fundamental. Its beauty, elegance, and precision may sometimes appear to be cold or inhuman and yet even very young children can gain great pleasure from working and solving problems within its domain.

Learning is a highly complex process and has characteristics which are both social and individual in nature. Most of us can think back to occasions when we struggled with a piece of mathematics on our own before experiencing a sudden flash of insight and the warm glow of understanding. Mathematical knowledge may often seem to have a highly personal nature as if we had created it for ourselves. However, mathematics is usually taught to large groups of pupils who are asked to arrive at a common understanding of an accepted body of knowledge.

The teacher’s creative and demanding role is to mediate between the contrasting demands of mathematical knowledge, the individual pupil, and the social situation to provide a mathematical education which will meet the needs of the individual child today and the adult in a future which we may not know. The complex nature of this task requires the exercise of professional judgement and continuous, on the spot, decision making from a creative teacher in a manner which cannot be prescribed from outside the classroom.

Although teachers rightly exercise a great deal of professional freedom within their classrooms about what and how they teach, they operate within a framework of attainment targets, programmes of study, commercially produced courses and statutory examinations which constrain their choices and focus their attention. In this chapter we will analyse that framework and begin to consider some of the opportunities for effective teaching which are presented. This chapter is introductory in character and many of the issues raised here will be treated in greater depth in following chapters.

Objectives

By the end of this chapter you will:

• understand the structure of the National Curriculum for mathematics, its programmes of study (PoS), attainment targets (ATs) and key stages (KS);
• know the different forms of examination which are commonly in use at ages 16 and 18;
• be developing an awareness of the knowledge and understanding which can reasonably be expected of the average pupil at specific ages;
• be aware of the extent to which the National Curriculum and its associated systems of assessment can form a framework within which professional judgement may be exercised in the development of creative approaches to meet the educational needs of pupils.

AN OVERVIEW OF THE NATIONAL CURRICULUM

The degree of central control over the curriculum and the conduct of teaching has varied considerably, but until the last quarter of the twentieth century the trend was towards local autonomy. For example, following the 1944 Education Act there was only one compulsory subject—religious education. George Tomlinson, Labour Minister of Education from 1947 to 1951 is alleged to have claimed ‘The Minister knows nowt about curriculum’ (Geen 1998:1)—a sentiment which many teachers but few Ministers have shared in the years since! Until the 1980s, Ministers concerned themselves with structural issues such as whether or not schools should be comprehensive and left decisions on the curriculum largely to the professionals.

Until quite recently, although the school curriculum was technically in the control of local authorities, in practice it was determined by head teachers in consultation with their governing bodies who could add or remove subjects or topics as they thought appropriate (Geen 1998). During the 1970s, however, a period of growing public disquiet over standards led to the famous 1976 Ruskin College speech by the then Prime Minister James Callaghan. ‘The great debate’ on education has continued to this day. A major committee of enquiry was set up in 1978 ‘to consider the teaching of mathematics in primary and secondary schools’ which reported 4 years later with recommendations which were reflected in the reforms which followed and may still be seen in the structure of the mathematics curriculum today (Cockcroft 1982).

Governments first began to take central control of teaching and learning in schools during the introduction of the new GCSE examinations. These were first awarded in 1988 and replaced the old O levels and CSEs. This required no legislation because, although the certificates were awarded by independent examination boards, they were countersigned by an Under Secretary in the Department of Education and Science. This previously unrecognized power enabled the then Secretary of State Keith Joseph to influence greatly the nature of the new GCSE. He was thus able to begin to control the curriculum and to some extent the style of teaching in secondary schools through the format of the new examination (Daugherty 1994).

The 1988 Education Reform Act which followed was one of the biggest single pieces of legislation of the twentieth century and provided the legal framework for the National Curriculum. Although the teaching unions were involved in an acrimonious dispute about pay and conditions at the time, both GCSE and the National Curriculum were generally welcomed by the profession in principle, although some were concerned that it was too prescriptive. There were also concerns about practicality because, although the curriculum was intended originally to require only 60 per cent of available time, it demanded that all pupils study ten subjects (eleven in Wales as a consequence of the inclusion of Welsh). As it was phased in during the late 1980s and early 1990s it became increasingly clear that it was overloaded and that some of the suggested plans for its assessment were impractical (Tanner 1992b).

Many amendments were made to the curriculum and its associated assessment during the first few years and, following a union boycott of the assessment arrangements, the Government ordered a full-scale review (Dearing 1993). This resulted in a new. simplified curriculum which was introduced in September 1995 with a promise that in the interests of stability there would be no further change before the year 2000.

The new curriculum for the year 2000 and beyond aims, first, to provide opportunities for all pupils to learn and to achieve and. second, to promote pupils’ spiritual, moral, social, and cultural development preparing them for the opportunities, responsibilities, and experiences of life (DfEE/QCA 1999b: Foreword). These two aims are interdependent because, as we will discuss in later chapters, the social and moral development of pupils influences their learning potential significantly. Clearly a centrally imposed curriculum is unable to achieve these aims by itself- motivated, professional teachers with effective practical skills are required to interact with children and mediate between curriculum aims and pupils’ individual human needs and ambitions. The curriculum does, however, fulfil four significant purposes:

• to establish an entitlement for all pupils;
• to establish standards and expectations;
• to promote continuity and coherence; and
• to promote public understanding.

(DfEE/QCA 1999b)

Task 1.1 The scope of the curriculum

The National Curriculum is expressed in terms of subjects. Imagine a typical school week of 25 hours spread over 5 days (i.e. 5 hours per day).

• Try to decide which subjects you would teach to a middle-ability year-9 class in an inner-city school.
• Should it make a difference if the class is of very high or very low ability?
• Should it make a difference if the school is in an affluent suburb?
• What proportion of the time have you granted to mathematics? How do you justify this?

Advice which had been offered to schools at the start of the decade had emphasized the rights of all children to access a curriculum which was broad and balanced no matter what their race, class, or sex. Without this entitlement enshrined in law. there was a concern that the curriculum for some pupils might be based on stereotypical and sometimes impoverished expectations. For example, girls might not be encouraged to study physics, boys might not learn foreign languages, inner-city pupils might not be expected to appreciate literature, highability pupils might not experience design technology, low-ability pupils might be discouraged from learning about science. Thus the demands of high culture, expressed through a traditional subject structure, are imposed nationally regardless of local conditions.

The National Curriculum does not dictate the hours to be granted to each subject, or even whether the subjects are taught separately from each other, but it does specify an entitlement which should be provided for the vast majority of pupils. In certain circumstances it is possible to ‘disapply’ up to two specified National Curriculum subjects for any one pupil but in such circumstances the Qualifications and Curriculum Authority (QCA) must be informed.

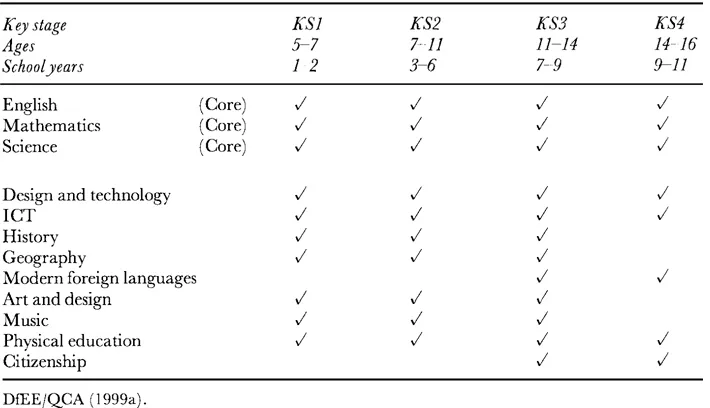
The curriculum is divided into four key stages associated with various ages and school years. At each key stage certain ‘core’ and ‘foundation’ subjects must be studied as shown in Table 1.1.

In addition to the subjects above, all pupils must study religious education. English, mathematics and science are described as ‘core’ subjects and occupy a privileged place in the curriculum. Pupils are expected to study core courses to GCSE level. In Scotland. Wales, and Northern Ireland dilferent National Curricula apply, reflecting the different cultural aims, ambitions, and contexts of those nations. For example, in Wales, Welsh is a ‘core’ subject in Welsh medium schools and a foundation subject in all other schools. As control of education has been devolved to the constituent national assemblies of the United Kingdom, further divergence is to be expected in the years to come.

The National Curriculum for mathematics has been the subject of significant disputation and political argument during its short history and consequently has been through several transformations. The disputes still continue and are generally focused on the nature of the subject itself and our aims in teaching it. As mentioned above, mathematics has a privileged position in the curriculum and it is appropriate for you to pause and consider why that might be.

Task 1.2 Aims of mathematics teaching

This task asks you to consider three issues:

• Why should mathematics be a core subject?
• What is mathematics essentially about?
• What should mathematics teaching emphasize?

The privileged position occupied by mathematics in the national curricula of most countries is due largely to its perceived usefulness. Unfortunately, since the 1970s, it has become increasingly clear that employers, school inspectors, and others are dissatisfied with the inability of school leavers to transfer the knowledge and skills taught in mathematics lessons to other contexts in the workplace and in everyday life (e.g. DES 1979). Research has shown (Lave 1988; Nunes et al. 1993) that in ‘real life’ situations school-learned procedures are unlikely to be used. Furthermore, much of the mathematics which is taught to all children in secondary schools has no obvious justification in everyday life although it is used as a tool by a minority of students at higher levels. For example: when did you last factorize a quadratic equation in the supermarket?

Table 1.1 The core and foundation subjects for each key stage.

Mathematics is an essential part of our culture and deserves a place in the curriculum for its own sake. We can enjoy its elegance and beauty in the same way as we might enjoy fine art. Mathematics teaching will have failed if pupils never experience the joy of mathematics. People enjoy solving problems. However, it should not justify its core position on those grounds alone. Mathematics provides a window for looking at the world and a framework for solving problems. In a democratic society all citizens require insight into such processes.

The debate continues to this day between those who see mathematics as a form of high culture, emphasizing abstract algebra and formal proof, focused inwards on itself (e.g. Gardiner in Neumark 1995) and those who see it as a practical and useful human construction gaining its status from its power to explain, organize, and change our world (e.g. Burton 1994). We would not wish to underemphasize either aspect, but we recognize that it is not yet fulfilling its potential as a powerful problem-solving tool for many of our pupils.

The following ‘indispensable’ aims for teaching mathematics to all pupils (DES 1985) influenced greatly the development of the new GCSE examination and the National Curriculum orders for mathematics. It was suggested that teaching at all levels should offer opportunities for pupils to experience:

• mathematics as an essential element of communication;
• mathematics as a powerful tool;
• an appreciation of relationships within mathematics;
• an awareness of the fascination of mathematics;
• imagination, initiative, and flexibility of mind in mathematics;
• working in a systematic way;
• working independently;
• working cooperatively;
• in-depth study; and
• confidence in their own mathematical abilities.

(DES 1985)

The aims were generally well received, although it was clear to many that turning such aims into a practical curriculum was going to require considerable development in school practices.

Like the other academic subjects, mathematics in the National Curriculum is described in terms of PoS and ATs. The PoS set out what should be taught to pupils and the ATs set out expected standards of attainment. The orders are not intended to dictate to schools how to teach the subject or how to arrange their teaching—it is for schools to determine how to plan to include the PoS within their curriculum (DfEE/QCA 1999b). However, although QCA claims that overall the latest programmes of study are less prescriptive, the new mathematics orders are far more detailed than previous orders. Detailed advice about the organization of teaching and learning in primary schools is also provided by the National Numeracy and Literacy Strategies.

Task 1.3 defining the PoS and ATs

For much of its existence mathematics has been expressed through five PoS and four or five ATs.

• If you were to divide the mathematics curriculum into four or five elements for teaching and assessment, how would you do it? Make a list of your own four or five titles for PoS and ATs.

The earliest version of the orders for mathematics had fourteen PoS and ATs (DES/WO 1989). This unmanageable excess was reduced to five PoS and ATs in the 1991 proposals (DES/WO 1991) and although the format and number of components has changed over the interven...

Table of contents

• Cover Page
• Title Page
• Copyright Page
• Abbreviations
• Preface
• 1: The National Curriculum A Framework for Teaching
• 2: What Makes A Good Mathematics Lesson?
• 3: Managing the Mathematics Classroom
• 4: Planning and Evaluating A Mathematics Lesson
• 5: Effective Teaching Approaches
• 6: Misconceptions and Planning How to Deal with Them
• 7 Learning to Think Mathematically: Using and Applying Mathematics
• 8: Mathematics in the Primary School
• 9: Numeracy in the Secondary School
• 10: Role of the Calculator in Learning Mathematics
• 11: Learning with and about ICT
• 12: Assessment and Learning
• 13: Evaluating and Developing Your Teaching
• Bibliography