Logic And Declarative Language

M. Downward

• Publisher: Routledge
• Year: 2004
• eBook ISBN: 9781135735852
• Topic: Informatica
• Subtopic: Informatica generale

Logic has acquired a reputation for difficulty, perhaps because many of the approaches adopted have been more suitable for mathematicians than computer scientists. This book shows that the subject is not inherently difficult and that the connections between logic and declarative language are straightforward. Many exercises have been included in the hope that these will lead to a much greater confidence in manual proofs, therefore leading to a greater confidence in automated proofs.

Part One

Logic without equality

Chapter One

Propositional logic

1.1 Syntax of Propositional Logic

A formal system consists of a set of symbols called an alphabet and a set of rules describing the way in which these symbols may be joined together to form strings of symbols. Our initial formal system is built from the following alphabet:

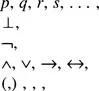
Symbols p, q, r, s, … represent an infinite number of atomic statements in the alphabet and may be seen as the building blocks of propositions. Three rows of symbols then show logical connectives that bind these atomic elements together according to the following rules:

a.	Symbols ⊥, p, q, r, s, … are themselves propositions.
b.	If A is a proposition then ¬A is also a proposition.
c.	If A and B are both propositions then A ∧ B, A ∨ B, A → B, and A ↔ B are also propositions.
d.	Strings of symbols not built up according to these rules are not propositions.

Unlike the atomic statement symbols p, q, r, …, symbols A and B represent any proposition and are not themselves part of the formal system being described. Symbols of this kind are often called metasymbols. The rules above define the number of arguments that each logical connective requires to produce a correctly formed proposition, producing a form of valency called the arity. Statement symbols p, q, r, … and the connective ⊥ are themselves propositions and thus have an arity of zero. A zero-arity connective might at this point seem a little fraudulent, but later we shall see that it does have properties in common with the other connectives. Only one connective symbol is defined with an arity of one, limiting the form of propositions that might be constructed from this symbol and atomic statement symbols. Increasingly large propositions may be constructed by the repeated attachment of this connective to a simple atomic statement as follows:

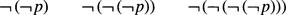
or to the special connective ⊥, e.g. ¬⊥, ¬(¬(⊥)). All remaining connectives are defined to be of arity two, giving propositions of the form

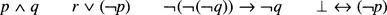
with simple or negated atomic statements. Such connectives may take arguments that are themselves formed from arity-two connectives, creating propositions such as

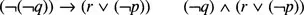
Parentheses are defined as part of the formal system to record the order in which a proposition is constructed from its atomic symbols. A proposition might be built from atomic statements p and q as follows:

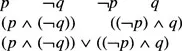
but if the same starting propositions are combined in a different order, a different proposition is obtained:

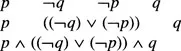
In order to reduce the number of brackets used in formulas a precedence order for arity one and two connectives is defined as follows:

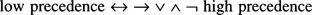
Connectives with the highest precedence bind most tightly to the objects that they connect. Thus ¬p ∧ q is understood to mean (¬p) ∧ q because a ¬ symbol has greater precedence than a ∧ symbol. Explicit bracketing would have to be included if the alternative proposition, ¬(p ∧ q), were intended. Similarly, proposition p ∧¬q ∨ ¬p ∧ q represents the first of the two examples constructed above and brackets would have to be retained to represent the second possibility. Symbol ∧ has a higher precedence than →, so the formula p ∧ q → r is assumed to represent (p ∧ q) → r, a formula in which connective ∧ is first applied to statements p and q then this proposition itself becomes an argument. The alternative proposition, p ∧(q → r) requires brackets to overide the precedence rule.

Sometimes the legal or allowed propositions are called well-formed propositions or well-formed formulas, but we shall simply call them propositions or formulas because we have no interest in constructions that are not well formed. An ill-formed formula such as p ∧ ∨ q looks odd, even to the inexperienced eye, so no great analysis is required to remove such problems. In fact, an algorithm that decides whether or not a given proposition is well formed may be written, and the proposition property is said to be decidable. All it requires is a procedure that breaks propositions into symbols and arguments according to the formation rules until only statement symbols or the constant ⊥ remain.

At this poin...

Table of contents

• Cover
• Half Title
• Title Page
• Copyright Page
• Table of Contents
• Preface
• Introduction
• Part One: Logic without equality
• Part Two: Logic with equality
• Bibliography
• Index