Frames, Fields, and Contrasts

New Essays in Semantic and Lexical Organization

Adrienne Lehrer, Eva Feder Kittay, Richard Lehrer, Adrienne Lehrer, Eva Feder Kittay, Richard Lehrer

• Publisher: Routledge
• Year: 2012
• Print ISBN: 9781138156388
• eBook ISBN: 9781136475801
• Topic: Languages & Linguistics
• Subtopic: Linguistics
• Index: Languages & Linguistics

Recently, there has been a surge of interest in the lexicon. The demand for a fuller and more adequate understanding of lexical meaning required by developments in computational linguistics, artificial intelligence, and cognitive science has stimulated a refocused interest in linguistics, psychology, and philosophy. Different disciplines have studied lexical structure from their own vantage points, and because scholars have only intermittently communicated across disciplines, there has been little recognition that there is a common subject matter. The conference on which this volume is based brought together interested thinkers across the disciplines of linguistics, philosophy, psychology, and computer science to exchange ideas, discuss a range of questions and approaches to the topic, consider alternative research strategies and methodologies, and formulate interdisciplinary hypotheses concerning lexical organization. The essay subjects discussed include:

* alternative and complementary conceptions of the structure of the lexicon,

* the nature of semantic relations and of polysemy,

* the relation between meanings, concepts, and lexical organization,

* critiques of truth-semantics and referential theories of meaning,

* computational accounts of lexical information and structure, and

* the advantages of thinking of the lexicon as ordered.

I

PRINCIPLES OF ORGANIZATION

1	Frames, Concepts, and Conceptual Fields

Lawrence W. Barsalou
University of Chicago

In this chapter I propose that frames provide the fundamental representation of knowledge in human cognition. In the first section, I raise problems with the feature list representations often found in theories of knowledge, and I sketch the solutions that frames provide to them. In the second section, I examine the three fundamental components of frames: attribute-value sets, structural invariants, and constraints. Because frames also represent the attributes, values, structural invariants, and constraints within a frame, the mechanism that constructs frames builds them recursively. The frame theory I propose borrows heavily from previous frame theories, although its collection of representational components is somewhat unique. Furthermore, frame theorists generally assume that frames are rigid configurations of independent attributes, whereas I propose that frames are dynamic relational structures whose form is flexible and context dependent. In the third section, I illustrate how frames support a wide variety of representational tasks central to conceptual processing in natural and artificial intelligence. Frames can represent exemplars and propositions, prototypes and membership, subordinates and taxonomies. Frames can also represent conceptual combinations, event sequences, rules, and plans. In the fourth section, I show how frames define the extent of conceptual fields and how they provide a powerful productive mechanism for generating specific concepts within a field.

FEATURE LIST REPRESENTATIONS OF CATEGORIES

Before proceeding to a detailed discussion of frames, I first discuss their most obvious competitor—feature list representations. Later, we see that frames remedy the fundamental problems of feature lists. Many theories across the cognitive sciences adopt feature list representations of categories. For example, work on natural categories and semantic memory in the 1970s typically employed feature list representations. Figure 1.1 contains examples of feature lists from the 1975 technical report that preceded Rosch, Mervis, Gray, Johnson, and Boyes-Braem's (1976) paper on basic level categories. As can be seen, each category representation is a list of features that subjects typically produce for the category, where a feature is any characteristic that category members may possess. Rosch and Mervis (1975) similarly constructed feature list representations of categories, as did Ashcraft (1978), Glass and Holyoak (1975), and Hampton (1979). Many other researchers did not collect feature lists explicitly from subjects but nevertheless assumed feature lists in theoretical modeling. In the semantic memory literature, feature comparison models assumed that semantic decisions involve the comparison of feature lists, as in McCloskey and Glucksberg (1979), Meyer (1970), Smith, Shoben, and Rips (1974), and A. Tversky (1977) (see also Wyer & Srull, 1986, in the social cognition literature). Barsalou and Hale (in press) review the wide variety of forms that feature lists take in categorization models.

More recently, connectionist models have embedded feature lists in dynamic networks (e.g., McClelland & Rumelhart, 1986; Rumelhart & McClelland, 1986). Rather than being independent, features in a connectionist system become intercorrelated, with excitatory relations developing between features that typically cooccur, and inhibitory relations developing between features that do not. In Fig. 1.1, each feature would be related to every other feature in its list, with some relations being excitatory and others being inhibitory. During categorization, input features activate correlated features and inhibit all others. As input features vary, they activate different feature subsets. Whereas traditional models represent a category with its entire feature list on every occasion, connectionist models represent a category dynamically with different feature subsets in different contexts.

BIRD	APPLE	SOCKS
feathers	seeds	you wear it
wings	sweet	keeps you warm
beak	you eat it	heel
legs	stem	toe
feet	core	cotton
eyes	skin	wool
tail	juicy	multicolored
head	round	worn on feet
claws	grows on trees	come in pairs
lays eggs
nests
flies
chirps
eats worms and flies

FIG. 1.1. Examples of feature lists for bird, apple, and socks from Rosch, Mervis, Gray, Johnson, and Boyes-Braem (1975). Copyright (1975 ) by the American Psychological Association. Reprinted by permission.

In principle, numerous theories in psychology and linguistics assume that representations contain more than feature lists. In many cases, however, the additional structure—which tends to be frame-like—remains implicit theoretically and receives little attention empirically. As a result, these representations essentially reduce to feature lists. Consider work on artificial category learning in cognitive psychology. Typically, this work assumes the presence of frames in category representations. As described in much more detail shortly, a frame includes a cooccurring set of abstract attributes that adopt different values across exemplars. To see this, consider the category structures in Fig. 1.2, adapted from artificial categories in Medin and Schaffer (1978, p. 213). Notice that each exemplar in a category has one value on each of four attributes: color, form, size, and position. The frame in each category is this cooccurring set of abstract attributes, which take different values across category members. Work on artificial categories almost always uses frames in this manner to define category structures, as in the work of Estes (1986), Gluck and Bower (1988), Hayes-Roth and Hayes-Roth (1977), Hintzman (1986), Homa (1978), McClelland and Rumelhart (1985), and Nosofsky (1984).

Although frames typically structure artificial categories, they have played little role empirically or theoretically. Empirically, frames are irrelevant because every exemplar in every category has values on the same attributes. As can be seen from Fig. 1.2, Categories A and B are not distinguished by attributes but instead by values of these attributes. Consequently, the focus of work on artificial categories has been on how subjects learn patterns of values that predict category membership. Although subjects must be learning the frame as well—the fact that all exemplars have values on the same attributes—this form of learning has generally remained unaddressed. Moreover, attribute learning must be important in category learning, because attributes often differ across categories. For example, car has attributes for engine and transmission, whereas dog has attributes for fur and temperament. Rather than categorizing entities solely on the basis of specific values, people often categorize them on the basis of more abstract attributes.

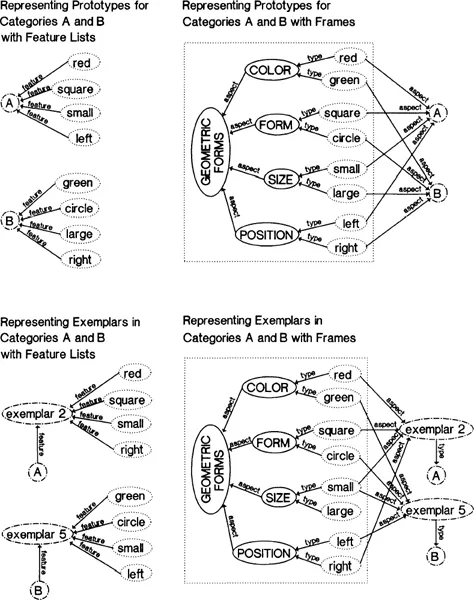
Theoretically, the frames that researchers use to define artificial categories have also received little attention. Theorists generally have nothing to say about the psychological status of these frames. Nor have researchers specified whether subjects view exemplar characteristics as attribute-value pairs or as a feature list. Figure 1.3 illustrates this distinction. In the upper left, prototype representations are essentially feature lists. Frames and the attribute-value sets that compose them are not represented explicitly but are only implicit in the representation. In contrast, the prototype representations in the upper right of Fig. 1.3 include an explicit frame (enclosed in the dotted box). The bottom half of Fig. 1.3 illustrates this distinction for exemplar representations. Because attributes are constant across artificial categories, and because attribute learning has not been of interest, the distinction between attributes and values has not been salient or explicit theoretically. As a result, representations in prototype and exemplar models have essentially been reduced to feature lists, such as those on the left of Fig. 1.3.

FIG. 1.2. The presence of frames in artificial categories. Adapted from Medin and Schaffer (1978, p. 213) by permission.

FIG. 1.3. Feature list and frame representations of prototypes (top) and of exemplars (bottom). Frames are enclosed in boxes.

In exemplar models and multidimensional spaces that weight attributes differentially, the distinction between attributes and values is more salient (e.g., Medin & Schaffer, 1978; Nosofsky, 1984; Shepard, 1974). However, these models nevertheless fail to specify how subjects know that particular characteristics of exemplars are values of one attribute and not another (e.g., how subjects know that triangle is a shape). Because these models include no explicit representation of attributes and their values, the ability to weight characteristics the same amount because they are values of the same attribute remains unspecified. Such an ability could rely on abstracted representations of attributes and their values; or it could rely on an embedded level of exemplar processing for categorizing characteristics as values of attribute categories.

Finally, work on componential analysis and semantic fields sometimes reduces semantic representations to feature lists. All of these theories assume that entries within a semantic field have values on abstract, shared attributes (e.g., Grandy, 1987; Katz, 1972; Kittay, 1987; Lehrer, 1974; Lyons, 1977; Miller & Johnson-Laird, 1976). However, semantic representations sometimes seem to include only values of these attributes. For example, bachelor might be represented as adult, male, human, and unmarried, failing to specify the attributes of age, sex, species, and marital status. Although these attributes are implicit, not specifying them explicitly implies that semantic representations are feature lists.

Evidence Against Feature Lists

The current psychological evidence against feature lists can be described alternatively as evidence for two structural properties of human knowledge: attribute-value sets and relations.

Evidence for Attribute-Value Sets. Rather than coexisting at a single “flat” level of analysis, the characteristics of exemplars typically form attribute-value sets, with some characteristics (values) being instances of other characteristics (attributes). For example, blue and green are values of color; swim and fly are values of locomotion; six-cylinder and eight-cylinder are values of automobile engine. Whereas features are independent representational components that constitute a single level of analysis, attribute-value sets are interrelated sets of representational components at two levels of analysis (at least). In this section, I review several sources of evidence that people encode exemplar characteristics as values of more abstract attributes, rather than as independent features.¹

Extensive literatures offer compelling evidence that animals use attribute-value sets in discrimination learning (see Sutherland & Mackintosh, 1971, for a review). Consider intradimensional transfer. Animals receive stimuli that vary on two attributes and are conditioned to expect reward following a particular value on one of them. For example, animals might receive stimuli that vary in color (blue versus yellow) and shape (circle versus oval). In the process, they might learn that blue signals reward and that yellow does not, with shape being irrelevant. Once animals learn this first discrimination, they learn...

Table of contents

• Front Cover
• Half Title
• Title Page
• Copyright
• Contents
• Dedication
• Introduction
• Part I: Principles Of Organization
• Part II: Concepts And Relations
• Part III: Specific Analyses
• Part IV: Computational Processes In The Lexicon
• Author Index
• Subject Index