Mathematics for Engineering

W Bolton

• Publisher: Routledge
• Year: 2012
• ISBN:
  9781136075490
• Edition: 2
• Topic: Mathematics
• Subtopic: Applied Mathematics
• Index: Mathematics

Mathematics for Engineering has been carefully designed to provide a maths course for a wide ability range, and does not go beyond the requirements of Advanced GNVQ. It is an ideal text for any pre-degree engineering course where students require revision of the basics and plenty of practice work. Bill Bolton introduces the key concepts through examples set firmly in engineering contexts, which students will find relevant and motivating. The second edition has been carefully matched to the Curriculum 2000 Advanced GNVQ units:
Applied Mathematics in Engineering (compulsory unit 5)
Further Mathematics for Engineering (Edexcel option unit 13)
Further Applied Mathematics for Engineering (AQA / City & Guilds option unit 25)A new introductory section on number and mensuration has been added, as well as a new section on series and some further material on applications of differentiation and definite integration.Bill Bolton is a leading author of college texts in engineering and other technical subjects. As well as being a lecturer for many years, he has also been Head of Research, Development and Monitoring at BTEC and acted as a consultant for the Further Education Unit.

Section E
Graphs

13 Graphs

14 Straight-line motion

15 Linear graphs

16 Polar coordinates

17 Alternating waveforms

The aims of this section are to enable the reader to:

• Plot graphs, choosing suitable scales and clearly marking data points.
• Plot graphs of equations: in particular, linear, exponential and sinusoidal.
• Determine gradients, intercepts and areas from graphs.
• Intepret graphs.
• Recognise the relationship between polar and Cartesian representations of points on a graph; plot polar graphs.
• Reduce non-linear laws to linear form.
• Use and interpret graphs in an engineering context.

This section is about the construction and interpretation of the types of graphs that are commonly encountered in engineering. Particular attention is directed towards linear, exponential and sinusoidal graphs; also, the linearisation of functions in order to obtain linear graphs.

Chapter 13 parallels the development of the mathematics in Section B. This section assumes dexterity with basic algebraic manipulation of equations. Chapter 14 shows the applications of Chapter 13 in a consideration of stright-line motion. Chapter 15 assumes that Chapter 12 and much of the algebra in Section B has ben covered. Chapter 16 assumes a basic knowledge of trigonometry and that the basics of Chapter 13 have been covered. Chapter 17 is an application of graphs in a study of alternating waveforms and their modelling by phasors.

13 Graphs

13.1 Introduction

Graphs are an indispensable element in engineering. They enable trends in experimental data to be more easily seen, and determined, than is possible by just looking at the numbers. Also, equations can be pictorially displayed by means of graphs and the relationships described by the equations more easily comprehended. This chapter is a review of the basic techniques of Cartesian graph drawing and the interpretation of such graphs. Functions which give linear and non-linear graphs are considered.

Chapter 14 looks at the application of graphs to at the engineering context of straight-line motion. Chapter 15 is consideration how relationships can be organised to give linear relationships.

13.2 Cartesian graphs

It is possible to specify the position of a point along a line from some zero point on that line by specifying its distance from the point. In order to specify which side of the zero point the distance is, distances measured to the right of the zero point are given as positive and distances to the left negative (Figure 13.1). Thus, with such a line, a distance specified as +2 is located 2 units to the right of the zero point.

Figure 13.1 Number line

If we want to specify the position of a point on a plane then we can use two such number lines at right angles to each other and intersecting at their zero points. The two lines are then called coordinate axes and their point of intersection the origin. The horizontal axis is called the x-axis and the vertical axis the y-axis (Figure 13.2). The positive half of the x-axis is to the right of the origin and the negative half to the left. The positive half of the y-axis is upwards from the origin and the negative half downwards.

Figure 13.2 Cartesian coordinates

To specify a point on the plane then we can specify its horizontal displacement and its vertical displacement from the origin, i.e. the intersection of the vertical and horizontal lines through the point with the x- and y-axes. If these intersections are x_A and y_A for some point A then the point is said to have the coordinates of (x_A, y_A). Such coordinates of points are called the Cartesian coordinates. The first number in such a pair of numbers is always the x-coordinate (or abscissa) and the second the y-coordinate (or ordinate)....

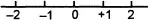
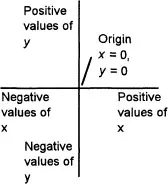
Table of contents

• Front Cover
• Half Title
• Title Page
• Copyright
• Contents
• preface
• Section A: Number and mensuration
• Section B: Algebra
• Section C: Further algebra
• Section D: Trigonometry
• Section E: Graphs
• Section F: Calculus
• Answers
• Index