Nonlinear Stochastic Control and Filtering with Engineering-oriented Complexities

Guoliang Wei, Zidong Wang, Wei Qian

• Publisher: CRC Press
• Year: 2016
• Print ISBN: 9780367574581
• eBook ISBN: 9781315350660
• Edition: 1
• Topic: Mathematics
• Subtopic: Differential Equations
• Index: Mathematics

Nonlinear Stochastic Control and Filtering with Engineering-oriented Complexities presents a series of control and filtering approaches for stochastic systems with traditional and emerging engineering-oriented complexities. The book begins with an overview of the relevant background, motivation, and research problems, and then:

• Discusses the robust stability and stabilization problems for a class of stochastic time-delay interval systems with nonlinear disturbances
• Investigates the robust stabilization and H? control problems for a class of stochastic time-delay uncertain systems with Markovian switching and nonlinear disturbances
• Explores the H? state estimator and H? output feedback controller design issues for stochastic time-delay systems with nonlinear disturbances, sensor nonlinearities, and Markovian jumping parameters
• Analyzes the H? performance for a general class of nonlinear stochastic systems with time delays, where the addressed systems are described by general stochastic functional differential equations
• Studies the filtering problem for a class of discrete-time stochastic nonlinear time-delay systems with missing measurement and stochastic disturbances
• Uses gain-scheduling techniques to tackle the probability-dependent control and filtering problems for time-varying nonlinear systems with incomplete information
• Evaluates the filtering problem for a class of discrete-time stochastic nonlinear networked control systems with multiple random communication delays and random packet losses
• Examines the filtering problem for a class of nonlinear genetic regulatory networks with state-dependent stochastic disturbances and state delays
• Considers the H? state estimation problem for a class of discrete-time complex networks with probabilistic missing measurements and randomly occurring coupling delays
• Addresses the H? synchronization control problem for a class of dynamical networks with randomly varying nonlinearities

Nonlinear Stochastic Control and Filtering with Engineering-oriented Complexities describes novel methodologies that can be applied extensively in lab simulations, field experiments, and real-world engineering practices. Thus, this text provides a valuable reference for researchers and professionals in the signal processing and control engineering communities.

1
Introduction

Contents

1. 1.1 Background, Motivation, and Research Problem
   1. 1.1.1 Engineering-Oriented Complexities
      1. 1.1.1.1 Traditional Engineering Phenomena
      2. 1.1.1.2 Randomly Occurring Incomplete Information
   2. 1.1.2 Systems with Engineering-Oriented Complexities
   3. 1.1.3 Analysis and Synthesis for Engineering-Oriented Complexities
2. 1.2 Outline

System complexities exist everywhere, with examples including time-delays, Markovian jump parameters, nonlinear disturbances, and parameter uncertainties. Such complexities are often referred to as traditional engineering phenomena that can be found in a variety of engineering systems, such as stochastic systems, linear parameter varying systems, genetic regulatory networks, networked control systems, and complex networks. Recently, with the rapid developments of networked systems, a new class of engineering-oriented complexities, namely, randomly occurring incomplete information, has been studied due to the fact that signal transmissions via networked systems are often hindered by the limited capacity of the devices. The phenomena falling in this group mainly include missing measurements [2, 172, 183], randomly occurring delays [168], randomly occurring sensor saturations [90, 182], randomly occurring nonlinearities [167, 192], and randomly occurring actuator faults [159, 190]. For more details about those randomly occurring incomplete information, we refer the readers to the survey paper [31] and [142].

When modeling the randomly occurring incomplete information, the Bernoulli distribution model has proven to be a flexible yet effective one that has been frequently employed, see, e.g., [186,187]. Accordingly, great effort has been devoted to better describe the randomly occurring incomplete information in the real world. It is worth mentioning that the authors of this book have successively put forward the general probabilistic model and the Bernoulli distribution model with time-varying probabilities to enrich the research in this area, which have received a significant amount of attention. In addition, it should be noticed that the randomly occurring incomplete information, together with tractional engineering phenomena, may potentially cause a lot of undesired problems that would seriously degrade the system performance. Hence, there is a great need to develop new strategies to deal with the engineering-oriented complexities.

Fortunately, during the past several decades, a great number of theories and techniques have been developed to handle the engineering-oriented complexities. Robust control/filtering, especially, H_∞ control/filtering is the most used one, since it can achieve the guaranteed performances with respect to the external disturbances. Besides, the Razumikhin-type methodology is an effective tool to deal with the stability issues of time-delay systems. Nevertheless, when it comes to the systems with randomly varying incomplete information, neither the robust control/filtering method nor the Razumikhin-type approach can provide the satisfactory control/filtering scheme, which motivates us to come up with a novel probability-dependent gain-scheduled technique to provide an elegant solution.

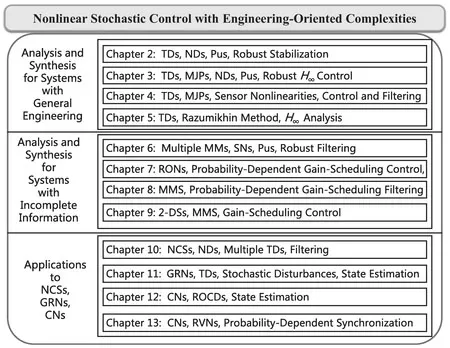
In this chapter, we focus on the control and filtering problems for nonlinear stochastic systems with the engineering-oriented complexities and aim to give a brief survey on some recent advances in this area. The engineering-oriented complexities addressed in this book include the traditional engineering phenomena (such as time-delays, Markovian jump parameters, nonlinearities, and parameter uncertainties, etc.) and randomly occurring incomplete information (such as missing measurements, randomly occurring nonlinearities, etc.). Secondly, several typical systems that are: often accompanied with engineering oriented complexities are introduced, and a series of analysis and synthesis techniques handling the engineering-oriented complexities is also discussed. Finally, the organization structure of this book is shown in Figure 1.1.

1.1 Background, Motivation, and Research Problem

1.1.1 Engineering-Oriented Complexities

This section discusses several engineering-oriented complexities that are studied thoroughly in this book. In what follows, the engineering-oriented complexities addressed in this book are categorized into two groups. The first one includes the traditional engineering phenomena, such as time-delays, Markovian jump parameters, nonlinearities, and parameter uncertainties etc., while another group involves the randomly occurring incomplete information. We only focus on two types of randomly occurring incomplete information (i.e., missing measurements and randomly occurring nonlinearities) in this section. For more details about the randomly occurring incomplete information, we refer the readers to the survey papers [31] and [142] where comprehensive discussions have been given.

FIGURE 1.1 The architecture of the book.

1.1.1.1 Traditional Engineering Phenomena

Time-Delays (TDs)

It is well known that time-delays are frequently encountered in practical systems, such as biology systems, engineering systems, traffic systems, and networked control systems [199]. The existence of time-delays may cause undesirable dynamic behaviors and add additional difficulties for the analysis and synthesis problems of nonlinear stochastic systems.

The commonly studied time-delays include constant delay, time-varying delay, distributed delay [99, 201], mixed time-delay [179, 185], sensor delay [175], randomly occurring time-delay [215], and randomly coupling time-delay in complex network [168]. In the past two decades, with the improvement of the computation capacity, the linear matrix inequalities (LMIs)-based methods have played an important role in the research on the general topic of time-delay systems; see, e.g., [12, 45, 123, 145, 146, 179, 186]. It is worth mentioning that, since the delay-dependent LMI techniques take the length of delays into account, the delay-dependent stability criteria are shown to be less conservative than the traditional delay-independent ones, especially when the time-delays are known and small; see, e.g., [21, 44, 54, 207, 221]. Accordingly, some improved delay-dependent methods have been given; see, e.g., [58–60, 206] for some up-to-date results. Recently, the stability analysis issues of nonlinear time-delay stochastic systems have received increasing research interests; see, e.g., [6, 38, 56, 109, 110, 132].

Markovian Jump Parameters (MJPs)

The real dynamical systems are often subject to abrupt variations in their structures, such as component failures or repairs, sudden environmental disturbances, changing subsystem interconnections, and operating in different point of a nonlinear plant [70, 144]. These complicated behaviors have led to the difficulties for modeling and analyzing the control systems. Fortunately, the Markov chain is a powerful tool to model some abrupt changes in the dynamics of the systems, where the switching parameter can be considered as a stochastic process with time evolution modeled by a Markov chain. Some examples of this type of phenomenon can be found in chemical process systems, economical systems, robotic control systems, etc. [50].

During the past decades, the problems of stability, stabilization, control, and filtering for systems with Markovian jump parameters have been extensively investigated; see, e.g., [14, 47, 98, 145, 146, 177, 181, 194, 220, 221]. To mention a few, the analysis and synthesis issues for uncertain systems with Markovian jump parameters have been studied in [47, 145, 146]. In [98, 177, 194, 220, 221], the filtering and control problems have been investigated for Markovian jump systems with or without nonlinear disturbances. The H_∞ control problem has been studied in [14], where the stochastic stability conditions have been proposed by using LMI technique. In [181], the stochastic stabilization problem has been investigated for systems with Markovian jump parameters and nonlinear exogenous disturbance inputs by solving a set of either LMIs or coupled quadratic matrix inequalities. So far, the analysis and synthesis problems have not yet been fully investigated for stochastic systems with Markovian jump parameters and time-delays.

Nonlinearities

It is well recognized that nonlinearities are inevitable and could not be eliminated thoroughly in many real-world systems, such as electrical circuits, mechanical systems, control systems, and other engineering systems [75]. In many papers, the nonlinearity is taken as the exogenous nonlinear disturbance (ND) input, which comes from the linearization process of an originally highly nonlinear plant [52, 170, 177]. In real-world applications, the nonlinearity is an inevitable feature for some sensors, which generally results from the harsh environments, such as uncontrollable elements (e.g., variations in flow rates, temperature, etc.) and aggressive conditions (e.g., corrosion, erosion, and fouling, etc.) [127], and this class of nonlinearities is often referred to as sensor nonlinearities. Because the sensor nonlinearities cannot be simply ignored and often lead to poor performances of the controlled system, the analysis and synthesis problems have received much research attention for various systems with sensor nonlinearities [15, 54, 78, 97]. On the otherhand, there are many different conditions for describing the nonlinearities. For example, sector-nonlinearity (also called sector-like nonlinearity), which is known to be quite general, includes the widely used Lipschitz condition as a special case. Moreover, the stochastic nonlinearity (SN) described by statistical means has drawn particular research focus, since it covers several well-studied nonlinearities in stochastic systems; see, e.g., [211, 219].

Parameter Uncertainties (PUs)

The parameter uncertainties serve as one important kind of complexity for system modeling and may arise from variations of the operating point, aging of the devices, identification errors, etc. Therefore, in the past decades, considerable attention has been devoted to address the analysis and synthesis problem for linear/nonlinear uncertain systems, and a large number of papers have been published; see [37, 52, 53, 100, 106, 125, 146, 160, 224] for some recent results. Besides, the robust H_∞ control problems have also been investigated for time-delay systems with parameter uncertainties; see, e.g., [47, 48, 147].

The parameter uncertainties can be generally classified into three types. The first one is the interval uncertainty, where the uncertain parameters take values in some certain intervals. The systems with interval uncertainties are known as interval systems, which have received considerable research attention to discuss the stability analysis and stabilization problems; see, e.g., [67, 114] and the references therein. The second one is the norm-bounded uncertainty, where the norm of the uncertainty matrix is often bounded by a real value. In fact, there are many physical systems in which the parameter uncertainties can be modeled in this manner, e.g., systems satisfying “matching conditions” [76]. During the past decades, the stabilization, control, and filtering problems have been extensively investigated for systems with norm-bounded uncertainties; for example, robust filtering [195], robust stabilization [76], robust H_∞ control [200], robust Kalman filtering [202], and nonfragile filtering [86]. Recently, the third type of uncertainties, namely, polytopic uncertainties, has gained increasing attention; see, e.g., [65, 208, 209], where the uncertainty has been described by a convex combination of N vertices. This representation is quite general and can encompass the well-known case of interval uncertainties; see [152, 189] for some latest results.

1.1.1.2 Randomly Occurring Incomplete Information

Missing Measurements (MMs)

In practical systems, due to various reasons, such as sensor temporal failure or network transmission delay/loss, the measurement signals may be subject to information missing. In case of information missing (called packet loss), the measurement output may contain noise only at certain time points. Such a measurement missing phenomenon usually occurs in a probabilistic way and has attracted considerable attention during the past few years; see, e.g., [149, 186] and the references therein. The Bernoulli distributed model has become a popular approach to model the measurement missing phenomenon, which is specified by a conditional probability distribution. As early as in [18, 122], such a model has been employed to synthesize the recursive filtering problems for systems with missing measurements. Recently, with the rapid developments of networked control systems, renewed effort has been devoted to this effective and flexible model; see, e.g., [186, 187, 228].

It should be pointed out that, in all aforementioned literature, the probability 0 is used to stand for an entire signal missing, and the probability 1 denotes the intactness (i.e., there is no signal missing at all), and all the sensors have the same missing probability. Such a description, however, does have its limitations, since it cannot cover some practical cases, for example, the case when only partial information is missing and the case when the individual sensor has different missing probabilities. Note that the latter case has been dealt with in [63, 64], where the minimum variance linear state estimators have been designed for linear systems with multiple sensors with different failure/delay rates. In [66, 195], a more general model describing the multiple missing measurements has been proposed and the filtering problems have been studied for stochastic systems. Recently, a probability-dependent gain-scheduling approach has been developed in [87, 193] to address the missing measurement with time-varying probabilities.

Randomly Occurring Nonlinearities (RONs)

Nowadays, the so-called randomly occurring nonlinearities (RONs) are prevalent in the networked control systems, such as the internet-based three-tank system for leakage fault diagnosis[31]. The RONs are a new kind of nonlinear disturbances that may appear intermittently in a random way due probably to random failures and repairs of the components, intermittently switching in the interconnections of subsystems, etc. The RONs have been initially introduced in [169, 185], where the global synchronization problems for complex networks have been discussed. Since then, a series of papers has been published concerning the control and filtering problems for systems with RONs; see, e.g., [28, 94, 108, 143, 168]. For example, in [108], a game theory approach has been applied to obtain the H_∞ controller when RONs occur. The dissipative control problem has investigated in [28] for systems with simultaneous presence of RONs, state saturations as well as multiple missing measurements. It should be noted that the RONs in [28, 94, 108, 143, 169, 185] have been assumed to satisfy a time-invariant Bernoulli distribution. Such an assumption will limit the application scope, since RONs usually appear with time-varying probabilities. Very recently, [168] has extended the RONs model in [169, 185] to the time-varying ones and designed the time-varying gain-scheduled controller based on the time-varying probabilities. Furthermore, [167] has considered the case that the RONs are varying between different kinds of nonlinearities according to the Bernoulli distribution, where the addressed phenomenon is named as randomly varying nonlinearities (RVNs).

1.1.2 Systems with Engineering-Oriented Complexities

It is well known that the engineering-oriented complexities ubiquitously exist in most of real systems. This book covers several typical systems that often encounter the engineering-oriented complexities, such as stochastic systems, linear parameter-varying systems, networked control systems, genetic regulatory networks and complex networks. In the following, we will introduce each of them in order to stir the reader’s i...

Table of contents

• Cover
• Half Title
• Title
• Copyright
• Contents
• List of Figures
• List of Tables
• Symbols
• Series Editor Foreword
• Series Editor
• Preface
• Authors
• 1 Introduction
• 2 Robust Stabilization for Stochastic Time-Delay Interval Systems
• 3 Robust H∞ Control for Markov Systems with Nonlinear Disturbance
• 4 H∞ Filtering and Control for Markov Systems with Sensor Nonlinearities
• 5 H∞ Analysis for Stochastic Differential Systems by Razumikhin Theory
• 6 Robust Filtering with Nonlinearities and Multiple Missing Measurements
• 7 Probability-Dependent Control with Randomly Occurring Nonlinearities
• 8 Probability-Dependent Filtering with Missing Measurements
• 9 Controller Design for 2-D Stochastic Nonlinear Roesser Model
• 10 Filtering for Networked Control Systems with Multiple Delays
• 11 State Estimation for Stochastic Delayed Gene Regulatory Networks
• 12 State Estimation for Complex Networks with ROCD
• 13 H∞ Synchronization for Complex Networks with RVN
• Bibliography
• Index