Frege, Dedekind, and Peano on the Foundations of Arithmetic (Routledge Revivals)

Donald Gillies

• Publisher: Routledge
• Year: 2013
• Print ISBN: 9780415668743
• eBook ISBN: 9781136721076
• Edition: 1
• Topic: Mathematics
• Subtopic: Arithmetic
• Index: Mathematics

First published in 1982, this reissue contains a critical exposition of the views of Frege, Dedekind and Peano on the foundations of arithmetic. The last quarter of the 19th century witnessed a remarkable growth of interest in the foundations of arithmetic. This work analyses both the reasons for this growth of interest within both mathematics and philosophy and the ways in which this study of the foundations of arithmetic led to new insights in philosophy and striking advances in logic.

This historical-critical study provides an excellent introduction to the problems of the philosophy of mathematics - problems which have wide implications for philosophy as a whole. This reissue will appeal to students of both mathematics and philosophy who wish to improve their knowledge of logic.

Chapter 1.
Kant’s Theory of Mathematics

Kant’s theory of mathematics depends on a pair of distinctions, namely:

(i) between a priori and a posteriori knowledge, and

(ii) between analytic and synthetic judgements.

The first distinction is really a traditional one. Kant explains it in (1781) Critique of Pure Reason A2/B3, p. 43 as follows:

“In what follows, therefore, we shall understand by a priori knowledge, not knowledge independent of this or that experience, but knowledge absolutely independent of all experience.”

A posteriori knowledge, however, does depend on experience.

The second distinction is really due to Kant himself — though there are traces of it in earlier authors. In (1781) Critique of Pure Reason, A6/B10, p. 48, the distinction is made as follows:

“Either the predicate B belongs to the subject A, as something which is (covertly) contained in this concept A; or B lies outside the concept A, although it does indeed stand in connection with it. In the one case I entitle the judgment analytic, in the other synthetic.”

Kant gives the following example to illustrate the distinction:

Analytic judgement: All Bodies are Extended.

Synthetic judgement: All Bodies are Heavy.

Kant believes that the concept of body contains the concept of extension, so that to talk of an unextended body would involve a contradiction. Thus “all bodies are extended” is analytic. On the other hand, although all bodies are indeed heavy, it is no way contradictory to conceive of a weightless body. Thus “all bodies are heavy” is synthetic.

This example is somewhat doubtful since Boscovich had proposed in 1759 that matter might consist of point atoms with no spatial extension, but acting on each other at a distance. Such point atoms appear to be conceivable, and, were they to exist, they would presumably be bodies of a kind. Thus the judgement “all bodies are extended” cannot, after all, be analytic. A favourite modern example “all bachelors are unmarried” seems better suited to illustrate Kant’s notion of analytic judgement.

Frege makes an interesting (and subsequently often repeated) criticism of Kant’s distinction between analytic and synthetic. He writes (1884) Foundations of Arithmetic, § 88, p. 100^e:

“On the basis of his definition, the division of judgements into analytic and synthetic is not exhaustive. What he is thinking of is the universal affirmative judgement; there, we can speak of a subject concept and ask — as his definition requires — whether the predicate concept is contained in it or not. But how can we do this, if the subject is an individual object? Or if the judgement is an existential one? In these cases there can simply be no question of a subject concept in KANT’s sense. He seems to think of concepts as defined by giving a simple list of characteristics in no special order; but of all ways of forming concepts, that is one of the least fruitful.”

The case where the subject is an individual object e.g. Socrates is mortal does not really pose serious difficulties, since Kant would presumably say that such judgements are synthetic. However, the case of existential judgements is more problematic.

The trouble is that Kant here, as everywhere else in the Critique of Pure Reason, assumes the correctness of Aristotelian logic. In particular he assumes that all propositions are of the subject—predicate form: S is P. It thus makes sense, at least where individual objects are not involved, to ask whether the predicate (P) is contained in the subject (S) or not.

However modern logic recognizes many propositions which are not of the subject—predicate form e.g.

says, existential propositions such as

It is not surprising that Frege should make this criticism since he is one of the founders of modern logic. To overcome the difficulty, Frege proposes a new definition of analytic which corresponds closely to Kant’s original intentions, but is adaptable to modern logic. We will consider this in the next chapter.

One of Kant’s principal claims is that mathematical judgements are synthetic a priori. Kant first argues, (1783) Prolegomena, §2, pp. 18–19, that:

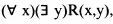
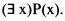
“…properly mathematical propositions are always judgements a priori, and not empirical, because they carry with them necessity, which cannot be taken from experience.”

He next argues that 7 + 5 = 12 is synthetic because, by analysis of the concept of the unification of 7 and 5, we cannot obtain the concept 12. As he puts it (op. cit. § 2, pp. 19–20):

“The concept of twelve is in no way already thought by merely thinking this unification of seven and five, and though I analyse my concept of such a possible sum as long as I please, I shall never find the twelve in it. We have to go outside these concepts and with the help of the intuition which corresponds to one of them, our five fingers for instance or (as SEGNER does in his Arithmetic) five points, add to the concept of seven, unit by unit, the five given in intuition. Thus we really amplify our concept by this proposition 7 + 5 = 12, and add to the first concept a new one which was not thought in it. That is to say, arithmetical propositions are always synthetic, of which we shall be the more clearly aware if we take rather larger numbers. For it is then obvious that however we might turn and twist our concept, we could never find the sum by means of mere analysis of our concepts without seeking the aid of intuition.”

The same applies to geometrical truths e.g. a straight line is the shortest distance between two points. ‘Straight’ is a qualitative concept and so we cannot, by analysis of concepts, obtain the quantitative fact that a straight line is the shortest distance between two points.

Kant does not of course deny that mathematics makes use of analytic truths e.g. (his example) the whole is greater than the part. His claim is rather that all significant mathematical truths are synthetic.

Having claimed that there exists synthetic a priori knowledge, Kant immediately raises the question of how such knowledge is possible. This is indeed a problem. If a judgement is synthetic i.e. not based on a mere analysis of concepts, it would appear to be ’about the world’, and hence only knowable on the basis of experience. How then can we know about the world a priori?. In order to explain Kant’s answer in the case of mathematics, we must next introduce and explain the Kantian concept of intuition.

For Kant, intuition means much the same as ‘sense—perception’ or ‘sensibility’. As he says, (1781) Critique of Pure Reason A51/B75 p. 93:

“Our nature is so constituted that our intuition can never be other than sensible; that is, it contains only the mode in which we are affected by objects.…Without sensibility no object would be given to us,…”

However (and this is where he differs from the empiricists), Kant holds that intuition contains not only a matter, originating from the thing which is being intuited, but also a. form supplied by the human mind. Indeed he claims, (1781) Critique of Pure Reason, A22/B36, p. 67, that:

“…there are two pure forms of sensible intuition, serving a principles of a priori knowledge, namely, space and time.”

Russell illustrates this theory, (1946) History of Western Philosophy, Book 3, Ch. XX Kant, p. 734, by the analogy of a man who, because he wears blue spectacles, sees everything blue. Similarly, according to Kant, we all wear spatio—temporal spectacles and so see everything in space and time. Things—in—themselves, however, are outside space and time.

The connection between this and mathematics is provided by the following quotation, (1783) Prolegomena, § 7, p. 36:

“But we find that all mathematical knowledge has this peculiarity, that it must first exhibit its concept in intuition, and do so a priori, in an intuition that is not empirical but pure; without this means mathematics cannot make a single step.”

What Kant means here can best be seen by considering geometry. In order to prove e.g. Pythagoras’ theorem, we must draw figures, or visualize such figures in our mind’s eye. That is, we must, in Kant’s terminology, exhibit the concepts (e.g. straight line, triangle, right angle, square, etc.) in intuition.

Similarly in arithmetic we have to proceed by counting — a process which takes time. However, as we saw in the earlier quotation, for arithmetic we need also spatial intuitions of such things as fingers or points. Apart from one brief reference to algebra, (1781) Critique of Pure Reason A734/B762 p. 590, Kant identifies mathematics with arithmetic and Euclidean geometry. He is thus able to link mathematics with intuitions of space and time in the above manner.

Kant’s theory of space and time as forms of intuition, and of things—in—themselves outside space and time, seems strange and exotic. Yet granted his basic premises, it follows almost of necessity. Kant, like most thinkers before the discovery of non—Euclidean geometry, regarded Euclid’s axioms as certain and necessary, and hence as not empirical. On this view, we know in advance that every object which we see and feel will obey these axioms. But how is such knowledge possible? It seems that it can only be explained on the assumption that spatial relations are supplied not by the object but by ourselves. To use Russell’s analogy, we are certain that the world will obey Euclid’s axioms only because we look at it through Euclidean spectacles.

Kant himself puts this line of thought as follows (1783) Prolegomena, § § 8 & 9, p. 38:

“But how can intuition of the object precede the object itself?

If our intuition had to be of such a nature that it represented things as they are in themselves, no intuition a priori would ever take place and intuition would be empirical everytime.…There is thus only one way in which it is possible for my intuition to precede the reality of the object and take place as knowledge a priori, namely if it contains nothing else than the form of sensibility which in me as subject precedes all real impressions through which I am affected by objects. That objects of the senses can only be intuited in accordance with this form of sensibility is something that I can know a priori.”

Perhaps the greatest blow to Kant’s theory of mathematics was the discovery of non—Euclidean geometries and the proof that such geometries are consistent relative to Euclidean geometry. These results suggested that we do not after all know a priori the true geometry of space, but have to determine the matter a posteriori, on the basis of experience. However, Frege does not attack Kant on these grounds. Indeed he defends the Kantian view of geometry. His criticisms, as we shall see in the next chapter, are directed against Kant’s theory of arithmetic.

Table of contents

• Cover
• Half Title
• Title Page
• Copyright Page
• Original Title Page
• Dedication
• Preface
• Table of Contents
• Introduction
• 1. Kant’s Theory of Mathematics
• 2. Frege’s Criticisms of Kant
• 3. Mill’s Theory of Mathematics
• 4. Frege’s Criticisms of Mill
• 5. The content of a statement of number is an assertion about a concept
• 6. Frege’s Platonism
• 7. Frege’s Logicism
• 8. Dedekind and Set Theory
• 9. Dedekind’s Development of Arithmetic
• 10. Peano’s Axioms. General Comparison of Frege, Dedekind, and Peano
• 11. Frege’s Begriffsschrift
• 12. Frege’s Grundgesetze, and Russell’s paradox
• Appendix I. On Notation
• Appendix II. On the Principle of Mathematical, or Complete, Induction
• References
• Index