Architecture of Mathematics

Simon Serovajsky

• Publisher: Chapman and Hall/CRC
• Year: 2020
• ISBN:
  9780429893537
• Edition: 1
• Topic: Matematica
• Subtopic: Matematica generale

Architecture of Mathematics describes the logical structure of Mathematics from its foundations to its real-world applications. It describes the many interweaving relationships between different areas of mathematics and its practical applications, and as such provides unique reading for professional mathematicians and nonmathematicians alike. This book can be a very important resource both for the teaching of mathematics and as a means to outline the research links between different subjects within and beyond the subject.

Features

• 
  
  

• All notions and properties are introduced logically and sequentially, to help the reader gradually build understanding.

• 
  
  

• Focusses on illustrative examples that explain the meaning of mathematical objects and their properties.

• 
  
  

• Suitable as a supplementary resource for teaching undergraduate mathematics, and as an aid to interdisciplinary research.

• 
  
  

• Forming the reader's understanding of Mathematics as a unified science, the book helps to increase his general mathematical culture.

Floor 1

Language

Science and technology, literature and art, religion and philosophy are different forms of human interaction with the world around them. The existence of the human in this world is always associated with the collection, storage and processing of diverse information. Any information is necessarily presented in a language, understandable for a certain persons. Therefore, the construction of any arbitrary formalized theory should be preceded by a characteristic of the language that is the only possible means of communication between individuals. Only having mastered to the proper degree this language, can we safely go on a long and difficult journey in an unfamiliar country, not being afraid to meet with its mysterious inhabitants.

The description of any language, natural or artificial, begins with an alphabet. This is a list of admissible letters for the considered language. The letters are combined under the rules of syntax in independent blocks, called words. Empowering words and phrases with some sense by the rules of semantics, we get statements that can be true or false.

Alphabet, syntax and semantics form three rooms of Floor (see Figure 1). This is not yet Mathematics, as we usually imagine it. There will be no distinctly definitions, no clearly defined concepts, no strict formulas, no serious theorems.

When moving on the first floor, we are forced to rely not on flawless logic, but on vague intuition. We try not to clearly define the rules of the game, but only to try to understand what game we are all the same entering. We will confine ourselves to a brief description of the situation, with a hope of some further understanding of these far from obvious problems. Only having risen high enough and looking around, moving from floor to floor, getting acquainted with local inhabitants (sets, numbers, structures, categories, etc.), entering into a direct conversation with them, we may, to some extent, master the language of Mathematics. Is it possible to learn some other natural language somehow differently?

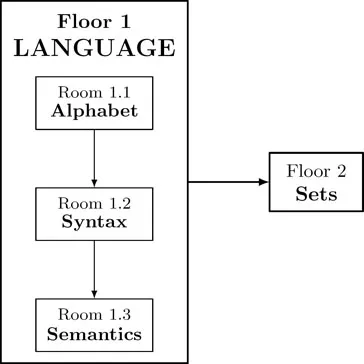
Room 1.1 Alphabet

The language is the necessary means of communication between individuals. Each statement in any language, regardless of its origin, is formulated using the elementary symbols that make up the alphabet.

Definition 1.1 An alphabet is a collection of admissible symbols that are called letters.

Remark 1.1 We understand that this definition is not fully correct. Particularly, the word “collection” is in fact the synonym with concept of the set that is fundamental for all subsequent constructions and is considered only on Floor 2. However, the presentation of set theory is necessarily carried out in a language that is characterized by a certain alphabet, and so the sets turn out to be secondary to the language. Besides, the word “symbol” is a synonym with concept of the letter and does not characterize it in any way. Another obvious drawback of this definition is associated with the mention in it of the language itself, which from the logical point of view is obtained only after the introduction of the alphabet and the rules of syntax and semantics. It remains for us to accept this sad situation and hope that we already have an intuitive idea of the alphabet.

Remark 1.2 By the position of Floor 2, we could say that the alphabet is a set, and its letters are the elements making up this set. In principle, any set can be interpreted as an alphabet, although this can hardly be of particular benefit. Particularly, the interpretation of the empty set defined on Floor 2 and the infinite sets (especially non-countable ones, see Floor 3) as an alphabet of a language would be strange enough. One usually understands an alphabet as a non-empty finite set of elements. However, the terms used here are meaningless so far. Therefore, we confine ourselves to what we have, namely, Definition 1.1.

To clarify the situation, let us consider an example related to natural language and, does not foretell seemingly no surprises.

Example 1.1 Latin alphabet. We have the easiest question. How many letters are there in the Latin alphabet? Any literate person will grin and confidently say that the Latin alphabet includes exactly 26 letters, namely, a, b,..., z. Such an answer does not seem to cause any objections. However, we are not interested in letters in a narrowly philological sense. We are trying to find out which characters are considered valid in the text based on the Latin alphabet, and therefore fall under the definition of the letter we have accepted. Can we assume that all the letters of the alphabet have already been listed? Are not other symbols used in Latin (English, French, etc.)? In particular, in any meaningful text, of course, there can also be capital letters A, B, ..., Z, which have their own peculiarities in language constructions, which means that they enter independently into our alphabet. Besides, we can also use in phrases the digits 0, 1, ..., 9. There are the letters too under Definition 1.1. However, our alphabet is not exhausted by this. All kinds of brackets, point, comma, dash, quotes, etc. also are the letters of this alphabet. These characters are also permissible and even necessary. Let us also recall different special symbols that have a completely definite meaning, for example, £ or ©. Remember the different mathematical symbols used sometimes in phrases. The text can sometimes contain letters of Greek, Russian, and other alphabets. Finally, the gap between the words in the sentence, i.e. the absence of any symbol, has some meaning, and therefore must be interpreted as a letter of the alphabet. Now we return to the initial question, how many letters are there in the Latin alphabet by Definition 1.1? It is hardly possible to give a clear answer to this quite innocuous question. However, there is no special need. It was important for us to emphasize that all symbols without exception, considered valid in the text in this language, should be recognized as letters of the alphabet. ◻

We will be interested, of course, not in the Latin (Greek, Russian) alphabet, but in the set of the symbols used in Mathematics. However, we do not presented their detailed list here. The necessary symbols will be introduced gradually in the course of the presentation of the material. As already noted, we are not concerned with the formal construction of Mathematics, but with the clarification of its logical structure. Therefore, now it was important for us only to note that the presentation of any formalized theory should begin with a description of the language, which is based on an alphabet. There is no need to begin a travel through the world of Mathematics with the declaration to the unfortunate traveler of a long and boring list of intricate symbols, the true meaning of which, often, will become clear only in the middle, if not at the end of the journey. Perhaps, it will not clear up at all...

By themselves, the letters do not yet form a language, just as bricks are just the building material from which buildings can be constructed. We still need to specify some formal rules that allow us to combine letters into words, and also be able to interpret the propositions. Thus, in order to get acquainted with the language, it is necessary to receive the an information about syntax and semantics.

Room 1.2 Syntax

The letters are elementary bricks that make up the language. Combining letters in blocks, we get a text that can be given a certain meaning. Thus, for the transfer of information, it is not the letters themselves that are important, but their combinations. As a result, we arrive at the following notion.

Definition 1.2 A word is an ordered sequence of letters that is admissible by the rules of syntax.

Remark 1.3 One uses also here the term formula, which is more natural for the language of Mathematics.

Remark 1.4 The word is not usually understood as any, but only a finite sequence of letters. However, the meaning of the finiteness of the object will be revealed only at the beginning of the Floor 3.

Remark 1.5 Using the word “sequence”, we mean that letters in a word are written in order one a...