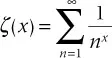Mathematical Reasoning

Patterns, Problems, Conjectures, and Proofs

Raymond Nickerson

• Publisher: Psychology Press
• Year: 2011
• ISBN:
  9781136945380
• Edition: 1
• Topic: Psychologie
• Subtopic: Geschichte & Theorie in der Psychologie

The development of mathematical competence -- both by humans as a species over millennia and by individuals over their lifetimes -- is a fascinating aspect of human cognition.

This book explores when and why the rudiments of mathematical capability first appeared among human beings, what its fundamental concepts are, and how and why it has grown into the richly branching complex of specialties that it is today. It discusses whether the 'truths' of mathematics are discoveries or inventions, and what prompts the emergence of concepts that appear to be descriptive of nothing in human experience. Also covered is the role of esthetics in mathematics: What exactly are mathematicians seeing when they describe a mathematical entity as 'beautiful'? There is discussion of whether mathematical disability is distinguishable from a general cognitive deficit and whether the potential for mathematical reasoning is best developed through instruction.

This volume is unique in the vast range of psychological questions it covers, as revealed in the work habits and products of numerous mathematicians. It provides fascinating reading for researchers and students with an interest in cognition in general and mathematical cognition in particular. Instructors of mathematics will also find the book's insights illuminating.

1

CHAPTER

What Is Mathematics?

Mathematics is not primarily a matter of plugging numbers into formulas and performing rote computations. It’s a way of thinking and questioning that may be unfamiliar to many of us, but is available to almost all of us. (Paulos, 1995, p. 3)

Mathematics is permanent revolution. (Kaplan & Kaplan, 2003, p. 262)

Many have tried, but nobody has really succeeded in defining mathematics; it is always something else. (Ulam, 1976, p. 273)

What is mathematics? Is it the “queen of the sciences,” as, thanks to Carl Frederich Gauss,^* it is often called? Or the “most original creation of the human spirit,” as Alfred North Whitehead† suggests (1956, p. 402)? Or, more prosaically, is it, as George Polya claims it appears to be to many students, “a set of rigid rules, some of which you should learn by heart before the final examinations, and all of which you should forget afterwards” (1954b, p. 157)? Is it the one area of knowledge in which absolute truth is possible? Or is it “fundamentally a human enterprise arising from human activities” (Lakoff & Núñez, 2000, p. 351), and therefore “a necessarily imperfect and revisable endeavor” (Dehaene, 1997, p. 247)? Do the truths of mathematics exist independently of the minds that discover them, or are they human inventions? Are they timeless and culture free? Or do they rest on assumptions that can differ over time and place? Are mathematics and logic one and the same? Does mathematics spring from logic, or logic from mathematics? Or is it the case, as Polkinghorne argues, that “mathematical truth is found to exceed the proving of theorems and to elude total capture in the confining meshes of any logical net”? (1998, p. 127). Is mathematics, as Bertrand Russell famously said, “the subject in which we never know what we are talking about, nor whether what we are saying is true” (1901/1956a, p. 1576)?

Not surprisingly, a diversity of opinions can be found regarding the answers to these and many related questions. In particular, as Hammond (1978) reminds us, “Mathematicians do not agree among themselves whether mathematics is invented or discovered, whether such a thing as mathematical reality exists or is illusory” (p. 16). In this book, I shall use the terms invention and discovery more or less interchangeably in reference to mathematical advances, having not found an entirely convincing argument to prefer one over the other. There are numerous views as to what constitutes the essence of mathematics, especially among mathematicians. A major purpose of this book is to explore some of those views and to catch a glimpse of what it means to reason mathematically.

I suspect that for many people, mathematics is synonymous with computation or calculation. Doing mathematics, according to this conception, amounts to executing certain operations on numbers—addition, subtraction, multiplication, division. More complex mathematics might involve still other operations—raising a number to a specified power, finding the nth root of a number, finding a number’s prime factors, integrating a function.

Computation is certainly an important aspect of mathematics and, for most of us, perhaps the aspect that has the greatest practical significance. Knowledge of how to perform the operations of basic arithmetic is what one needs in order to be able to make change, balance a checkbook, calculate the amount of a tip for service, make a budget, play cribbage, and so on. Moreover, the history of the development of computational techniques is an essential component of the story of how mathematics got to be what it is today. But, important as computation is, it plays a minor role, if any, in much of what serious mathematicians do when they are engaged in what they consider to be mathematical reasoning.

Whatever else may be said about mathematics, even the casual observer will be struck by the rich diversity of the subject matter it subsumes. Ogilvy (1956/1984) suggests that mathematics can be roughly divided into four main branches—number theory, algebra, geometry, and analysis—but each of these major branches subsumes many subspecialties, each of which can be portioned into narrower subsubspecialties. What is it that the myriad forms of mathematical activity have in common that justifies referring to them all with the same name?

Sternberg (1996) begins a commentary on the chapters of a book on the nature of mathematical thinking that he edited with Ben-Zeev (Sternberg & Ben-Zeev, 1996), with the observation that the chapters make it clear that “there is no consensus on what mathematical thinking is, nor even on the abilities or predispositions that underlie it” (p. 303). He cautions the futility of the hope of understanding mathematical thinking in terms of a set of features that are individually necessary and jointly sufficient to define it, and expresses doubt even of the possibility of characterizing it in terms of a prototype, as has proved to be effective with other complex concepts.

This seems right to me. There are many varieties of mathematical thinking. And mathematicians are a diverse lot of people, reflecting an unbounded assortment of interests, abilities, attitudes, and working styles. Nevertheless, there are, I believe, certain ideas that are especially descriptive of the doing of mathematics and that hold it together as a unified discipline. Among these are the ideas of pattern, problem solving, conjecture, and proof.

Mathematics as the Study of Pattern

Where there is life, there is pattern, and where there is pattern there is mathematics. (Barrow, 1995a, p. 230)

At the heart of mathematics is the search for regularity, for structure, for pattern. As Steen (1990) puts it, “Mathematics is an exploratory science that seeks to understand every kind of pattern—patterns that occur in nature, patterns invented by the human mind, and even patterns created by other patterns” (p. 8). And, as Whitehead (1911) and Hammond (1978) note, it is the most powerful technique for analyzing relations among patterns. Sometimes mathematics is referred to simply as “the science of patterns” (Devlin, 2000a, p. 3; Steen, 1988, p. 611).

The types of patterns that mathematicians look for and study include patterns of shapes, patterns of numbers, patterns in time, and patterns of patterns. What is the pattern of constant-radius spheres when they are packed in the most efficient way possible? What is the pattern that describes the distribution of prime numbers? How does one tell whether a pattern that describes a relationship between or among mathematical entities in all known instances is descriptive of the relationship generally? (For all cases checked, every even number greater than 2 is the sum of two primes; how does one know whether it is true of all numbers?) Is it possible to find a single pattern of relationships in the falling of a feather and a stone, and the motion of the moon around the Earth and that of the planets around the sun?

The detection of patterns has been of great interest to scientists as well as to mathematicians. At least one account of human cognition makes pattern recognition the fundamental basis of all thought (Margolis, 1987). That the same patterns are observed again and again in numerous contexts in nature—in crystals, in biological tissues, in structures built by organisms, in effects of physical forces on inanimate matter (Stevens, 1974)—demands an explanation. The importance of pattern in art is obvious; it is expressed in numerous ways, and one need not be a mathematician to appreciate or to produce it. Maor (1987) says of Johann Sebastian Bach and Maurits C. Escher: “Both had an acute sense for pattern, rhythm, and regularity—temporal regularity in Bach’s case, spatial in Escher’s. Though neither would admit it (or even be aware of it), both were experimental mathematicians of the highest rank” (p. 176). Hofstadter (1979) gives numerous examples of the role of pattern in the work of both men.

The detection of a local pattern, some regularity among a limited set of mathematical entities (numbers, shapes, functions), can be the stimulus to a search for a general principle from which the observed pattern would follow. Often such observations have prompted conjectures, and these conjectures sometimes have stood as challenges to generations of mathematicians who have sought to prove them and elevate them to theorem status. Cases in point include Gauss’s conjecture, made when he was 15, that the number of prime numbers between 1 and n is approximately n/log_e n; Christian Goldbach’s conjecture, dating from 1742, that every even number greater than 2 is the sum of two primes; Pierre de Fermat’s “last theorem,” that xⁿ + yⁿ = zⁿ is not solvable for n > 2; and Georg Riemann’s zeta conjecture. These conjectures and others will be noted again in subsequent chapters.

Unlike the conjectures of Gauss, Goldbach, and Fermat, that of Riemann—usually referred to as the Riemann hypothesis, is likely to appear arcane to nonmathematicians, but the—so far unsuccessful—search for a proof of it has been a quest of many first-rate mathematicians. For present purposes it suffices to note that the Riemann hypothesis has to do with the distribution of prime numbers and involves the zeta function,

first noted by Leonard Euler, and about which more is given in Chapter 3. To all appearances the distribution of primes is chaotic and completely unpredictable, but proof of the Riemann hypothesis would make it possible to locate easily a prime of any specified number of digits, and would have other implications for number theory as well. The interested reader is referred to a beautiful book-length treatment of the Riemann hypothesis by Marcus du Sautoy (2004), who, in the subtitle of his book, refers to the question of the distribution of primes as “the greatest mystery of mathematics.”

Local patterns do not always signal more general relationships, so one cannot simply extrapolate beyond what one has actually observed, unless one has the authority of a proof on which to base such an extrapolation. We will return to this point in Chapter 5, but will illustrate it now with an example from solid geometry. A convex deltahedron is a solid, all the faces of which are equilateral triangles of the same size. (The term deltahedron comes from the solid’s triangular face resembling the Greek letter delta.) The smallest possible deltahedron is a tetrahedron, and the largest is an icosahedron. These are the smallest (4-faced) and largest (20-faced) of the five Platonic solids. That it is impossible to make a solid with less than four equilateral triangles should be obvious. That it is impossible to make one with more than 20 such triangles follows from the necessity, in order to do so, to have six triangles meet at a corner (five meet at a corner in the icosahedron), and the only way to do this is to have all six be in the same plane. How many deltahedra should it be possible to make counting the smallest and largest possibilities?

Because every triangle has three sides and every edge of a deltahedron must be shared by two triangles, the finished shape with n triangles will have 3n/2 edges, and because the shape must have an integral number of edges, the number of triangles used, n, must be a multiple of 2. If we tried making a six-faced deltahedron, we would find it is possible to do so. We would also discover, if we tried, that we could make deltahedra with 8 faces, with 10, with 12, and so forth. At some point in this experiment, we might begin to suspect, perhaps even to convince ourselves, that deltahedra can be made with any even number of triangles between 4 and 20 inclusive. If we continued making these things, our confidence in this conjecture would probably be quite high by the time we succeeded in making 14- and 16-faced forms. But surprise! Try as we might, we would not succeed in making one with 18 faces.

In short, local regularities can be misleading. Inferring a general pattern from a local pattern is risky. If there is a general pattern, a local pattern will be observed, but the converse is not necessarily true, which is to say that if a local pattern is observed, a general pattern of which it is an instance may or may not exist. Not surprisingly, mathematicians are especially interested in finding patterns that are general; they take it as a challenge to distinguish between those that are and those that are not.

Mathematics as Problem Solving

As well as regarding mathematics as the study of patterns, mathematics can be viewed, pragmatically, as a vast collection of problems of certain types and of approaches that have proved to be effective in solving them. Pure mathematicians may not appreciate this view, but it is a viable one nevertheless. Some mathematicians see the essence of mathematics to be problem solving (Halmos, 1980; Polya, 1957, 1965). Casti (2001) puts it this way: “The real raison d’etre for the mathematician’s existence is simply to solve problems. So what mathematics really consists of is problems and solutions” (p. 3). The really “good” problems, in Casti’s view—those that become recognized as “mathematical mountaintops”—are those that challenge the best mathematical minds for centuries. Really good problems are really good, not only by virtue of being difficult, but because attempts to solve them commonly contribute to the development of whole new fields of mathematics. Casti’s selection of the five most famous mathematical problems of all time is shown in Table 1.1. More will be said about some of these problems in subsequent chapters.

TABLE 1.1 The Five Most Famous Mathematical Problems of All Time, According to Casti (2001)

1.	Determination of the solvability of a Diophantine equation. “To devise a process according to which it can be determined by a finite number of operations whether a Diophantine equation is solvable in rational integers” (p. 12). A Diophantine equation is a polynomial equation, all the constants and variables of which, as well as the solutions of interest, are integers.
2.	Proof of the four-color conjecture: The conjecture that four colors suffice to color a two-dimensional map so that no two contiguous regions have the same color.
3.	Proof of Cantor’s continuum hypothesis: There is no infinity between that of the natural numbers and that of the reals.
4.	Proof of Kepler’s conjecture: Face-centered cubic packing of spheres of the same radius is the optimal packing arrangement (yields the smallest ratio of unfilled-to-filled space).
5.	Proof of Fermat’s “last theorem”: The equation x^n+ y^n= z^nhas no solutions for n > 2.

A distinction is sometimes made between knowing mathematics and doing mathematics. Romberg (1994b) illustrates the distinction by drawing an analogy with the difference between having knowledge about other activities (flying an airplane, playing a musical instrument) and actively engaging in them. Schoenfeld (1994b) likens the doing of mathematics with the doing of science—“a ‘hands-on,’ data-based enterprise” with “a significant empirical component, one of data and discovery. What makes it mathematics rather than chemistry or physics or biology is the unique character of the objects being studied and the tools of the trade” (p. 58).

The nature of the problems that present themselves in pure and applied math may differ, but the need for problem solving spans the range from the purest to the most highly applied. Among other benefits, mathematical training gives one the ability to solve many complex problems in a stepwise fashion, by formulating the problems in such a way that the successive application of well-defined symbol transformation rules will take one from the problem statements to the expressions of the desired solutions.

There is the view too that one of the purposes that mathematics serves is to make problem solving—or reasoning more generally—easier or, in some cases, unnecessary. Austrian physicist-philosopher Ernst Mach (1906/1974) attributes to Joseph Louis Lagrange the objective, in his Méchanique analytique, “to dispose once and for all of the reasoning necessary to resolve mechanical problems, by embodying as much as possible of it in a single formula” (p. 561). Mach believed that Lagrange was successful in attaining this objective, that his method made it possible to deal with a class of problems mechanically and unthinkingly. “The mechanics of Lagrange,” Mach contends, “is a stupendous contribution to the economy of thought” (p. 562). It seems clear that discoveries of mathematical equations that are descriptive of relationships in the physical world have made reasoning about those relationships easier, or even perhaps unnecessary in some instances, but it seems equally clear that the same discoveries have had the effect of extending the range of reasoning, unburdening it in some respects and thereby enabling it to function at higher levels.

Mathematics as Making Conjectures

Quibbles aside, every theorem is born as a conjecture. Like the rest of us, the mathematicia...