Chaos, Noise and Fractals

E. Roy Pike, L .A. Lugiato, E. Roy Pike, L .A. Lugiato

• Publisher: CRC Press
• Year: 2020
• ISBN:
  9781000156911
• Edition: 1
• Topic: Mathematics
• Subtopic: Linear & Nonlinear Programming
• Index: Mathematics

The study of nonlinear dynamical systems has been gathering momentum since the late 1950s. It now constitutes one of the major research areas of modern theoretical physics. The twin themes of fractals and chaos, which are linked by attracting sets in chaotic systems that are fractal in structure, are currently generating a great deal of excitement. The degree of structure robustness in the presence of stochastic and quantum noise is thus a topic of interest. Chaos, Noise and Fractals discusses the role of fractals in quantum mechanics, the influence of phase noise in chaos and driven optical systems, and the arithmetic of chaos. The book represents a balanced overview of the field and is a worthy addition to the reading lists of researchers and students interested in any of the varied, and sometimes bizarre, aspects of this intriguing subject.

HYPERCHAOS AND 1/f SPECTRA IN NONLINEAR DYNAMICS

F T ARECCHI

1. INTRODUCTION

In the middle 1300 the following problem has been attributed to Johannes Buridanus, a philosopher at the University of Paris. Suppose a donkey is just halfway between two equivalent choices (e.g. two food baskets that we call F1 and F2). What will be its decision? In the solution attributed to Buridanus the donkey dies, having no elements to decide for either solution. The current modern solution, upon which most of statistical physics is built, is more optimistic. The initial condition between the two choices is an unstable one, like the maximum x=0 in a quartic potential well V(x)=−ax² +bx⁴ (a,b >0) and it would be left immediately once the donkey (taken as a material point initially at x=0) is coupled to the rest of the Universe, which provides for a thermal bath including fluctuations (even at zero temperature there would be quantum flunctuations).

Let us model the fluctuations as an additive white noise (no memory) source. If we use a discrete time approach and introduce an uncertainty Δx per step (the donkey’s feet have a finite size), there is a single time scale τ, that corresponding to the average first passage time through Δx. Afterwards, because of the uniqueness theorem for the solution of a differential problem, noise will not play any extrarole and the donkey will go either to F1 or F2. The time scale τ provides an exponential decay of correlations, that is, of the memory of the initial uncertainty and an associated Lorentzian power spectrum

$\text{G}\left(\text{ω}\right)\simeq \frac{1/\text{τ}}{{\text{ω}}^2+1/{\text{τ}}^2}$

(1)

As well known a log-log of (1) has two asymptotic straight lines, a high frequency one with a slope −2 (20 db/decade) and a horizontal one for low frequency, corresponding to lack of correlations (white spectrum). The two lines cross at ω = 1/τ. The long time lack of correlation is the basis of all Markoffian approaches to statistical physics.

Buridanus’ solution would be then wrong, since the donkey does not die but it performs a decision with a definite time scale.

These considerations where the basis of an approach to decay of unstable states motivated by an early experiment on a transient laser (Arecchi et al, 1967 and 1971) and then formalized in a general procedure (Arecchi et al, 1980 and 1982a).

If, however, still with the same two-valley potential (bistable solution) and in the presence of a white noise, we increase the number of degrees of freedom up to 3 in order to allow for a chaotic dynamics, then we observe experimentally, the possibility of jumps back and forth from a decision to the other one.

Aim of this paper is to show that this is equivalent to provide Buridanus’donkey with a fractal boundary between the two choices. Indeed an irregular rugged boundary can be crossed from several directions, and it will provide a large number of length scales rather than a single one Δχ, and hence a large number of time scales. This will be equivalent to the superposition of many Lorentzians spectra as (1), thus providing a power spectrum utterly different from a Lorentzian one. The donkey will keep a long memory of the initial uncertainty and it might die as expected by Buridanus.

In the following we approach the problem with reference to chaotic dynamics, offering a solution in terms of an elementary model.

2. NOISE INDUCED TRAPPING AT THE BOUNDARY BETWEEN TWO ATTRACTORS

Addition of random noise in a nonlinear dynamical system with more than one attractor may lead to 1/f spectra, provided that the basin boundary be fractal (Arecchi and Califano, 1986). Combining the features leading to deterministic chaos with a random noise is somewhat equivalent to a double randomness and we call “hyperchaos” such a situation. Indeed random-random walks in ordinary space, as diffusion in disordered systems, have shown a 1/f behavior (Sinai, 1982; Marinari et al, 1983). Thus, hyperchaos here introduced is a random-random walk in phase space, where in fact one of the two sources of complex behavior is due to the fractal structure arising from deterministic dynamics.

To evaluate the impact of the following arguments, I premise some historical remarks on 1/f spectra in nonlinear dynamics.

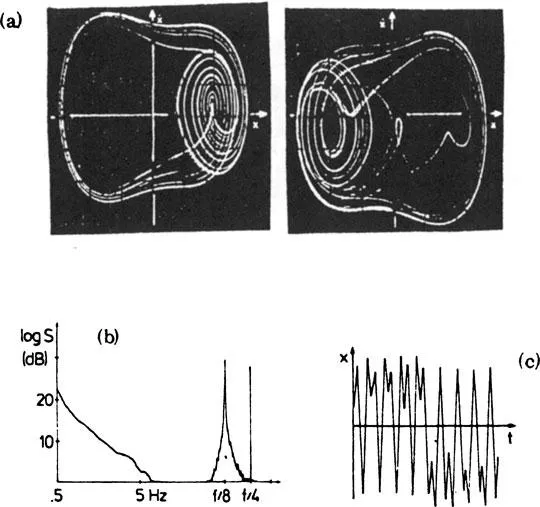
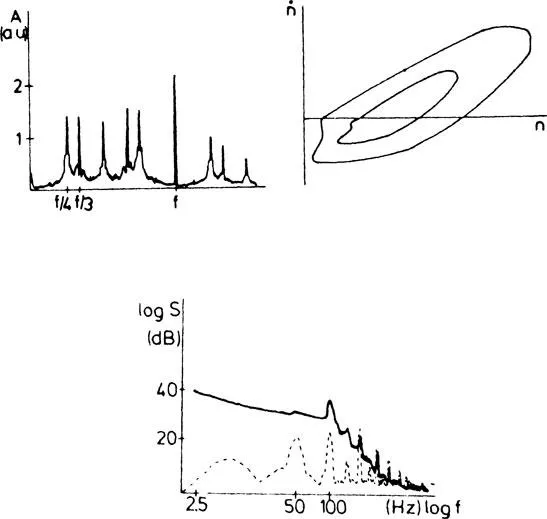
Some years ago it was discovered (Arecchi and Lisi, 1982) that in a nonlinear dynamical system with more than one attractor, introduction of random noise induces a hopping between different basins of attraction, giving rise to a low frequency spectral divergence, resembling the 1/f noise well known in many areas of physics (Fig. 1). Such a discovery was confirmed by a laser experiment implying two coexisting attractors (Arecchi et al, 1982b) (Fig. 2), and later the effect was observed in other areas as e.g. Josephson tunnel junctions (Miracky et al, 1983).

Figure 1 Electronic non linear forced oscillator obeying the law ẍ + _γ ẋ − ax + bx³ = Acos (2 π ft). Hopping between two attractors and associated 1/f spectrum in the purely bistable case, (a) Symmetric phase-space plots; (b) log-log spectrum showing the low frequency divergence, a broadened f/8 line, and a narrow f/4 line; (c) a sample of the x(t) plot.

The effect was questioned with two objections:

a) a noise induced jump across a boundary leads to a telegraph signal, hence to a single Lorentzian spectrum (Beasley et al, 1983);

b) a computer experiment yielded a power law only over a limited spectral range (Voss, 1983).

The questions were answered (Arecchi and Lisi, 1983) with a statement of the empirical conditions under which the 1/f spectra appeared, namely:

i) coexistence of at least two attractors (so called “generalized multistability” (Arecchi et al, 1982b)),

ii) presence of noise,

iii) some “strangeness” in the attractors.

As a matter of fact this third condition was rather vague. To make it more precise, two theoretical models were explored, namely, a one dimensional cubic iteration map with noise (Arecchi et al, 1984a) and a forced Duffing equation with noise (Arecchi et al, 1984b; Arecchi et al, 1985a). Both these papers disclose interesting features, bringing more light on the above assumption iii). Fig. 2 of Arecchi et al 1984a shows that the size of the 1/f spectral region increases with the r.m.s. of the applied noise, that is, with the probability of crossing the basin boundary by a noise-induced jump.

The numerical evaluation of Arecchi et al 1984b and Arecchi et al 1985a showed that for some control parameters the boundary between basins of attraction was an intricated set of points, through which it was impossible to draw a simple line. In such cases the noise was most effective in yielding low frequency spectra 1/f-like.

On the other hand a fundamental logical approach to the 1/f problem was based on the composition of a large number of Lorentzians (or elementary Markov processes with exponential decay) whose weights are log-normally distributed (Montroll and Shlesinger, 1982), thus fulfilling the relation

${\displaystyle {\int }_{{\text{γ}}_1}^{{\text{γ}}_2}\frac{\text{γ}}{{\text{ω}}^2+{\text{γ}}^2}\text{p}\left(\text{γ}\right)\text{dγ}}\simeq \text{const}\text{.}\text{x}{\frac{1}{\text{ω}}}^{,}$

(2)

provided p(γ) ~ 1/γ, and for the frequency range γ ₁≪ω≪ γ ₂

Figure 2 Bistability in a CO₂ laser with loss modulation. (a,b) coexistence of two attractors (period 3 and 4 respectively) high frequency spectrum around 100KHz, (c) comparison between the low frequency cut-off when the two attractors are stable (dashed line) and the low frequency divergence when noise is added (solid line).

Motivated by the rate processes considerations, which yielded a single Lorentzian for two attractors, we developed a kinetic model (Arecchi et al, 1984a) based on a single transition rate for each pair of attractors. In the case of M attractors, this yielded M-1 Lorentzians. To approximate the integra...