Basic Superfluids

Tony Guenault

• Publisher: CRC Press
• Year: 2002
• eBook ISBN: 9781135732356
• Topic: Physical Sciences
• Subtopic: Physics
• Index: Physics

Superfluidity is the jewel in the crown of low temperature physics. When temperatures are low enough, every substance in thermal equilibrium must become ordered. Since some materials remain fluid to the lowest temperatures, it is a fascinating question as to how this ordering can take place. One possibility is the formation of a superfluid state, a

Chapter 1
What happens at low temperatures?

Low temperature physicists have goals which are common to most human beings. They are looking for a quiet life! Perhaps regrettably, the state of perfect order and peace which they seek is not so much in their heads as in the physical world outside them. Fortunately, in this physical world, it turns out that the calming down of thermal vibrations at low temperatures does not merely bring a grey dullness and sameness to the properties of every form of matter. Rather, it allows the emergence of a whole range of new states of matter which unfold a surprising richness and excitement. Among these new states are the “superfluids”.

Superfluidity has been described as the jewel in the crown of low temperature physics. Superfluid states are characterised by the dominant influence of quantum mechanics on the large-scale thermal properties of the substance in question. As we shall see, superfluid states are observed in many systems. Examples are found in the superconductivity of many metals and some near-metals, in the extraordinary properties of the helium liquids, in neutron stars and in the behaviour of gaseous assemblies of cold alkali metal atoms.

1.1 ENTROPY, ORDERING AND THE THIRD LAW

What happens at a low enough temperature is that anything which is in thermal equilibrium must become ordered, ordered in the sense of organised. In other words it has zero entropy. That in essence is the content of the Third Law of Thermodynamics.

1.1.1 Ordering in a simple substance

Let us take nitrogen as a typical substance, one with few complications and in which no superfluid state is known. (We conveniently avoid remembering that N₂ molecules have internal structure, since that does not affect the argument here!) How does ordering take place as our nitrogen is cooled towards the absolute zero of temperature?

At room temperature nitrogen is of course a gas, which is a highly disordered state of matter. The gas has a high entropy. Furthermore when the temperature is increased, the molecules move even faster, the gas expands at constant pressure and it becomes more dilute and more disorganised. The entropy thus increases further. When the gas is cooled below room temperature the reverse happens. The molecules slow down and the volume occupied by the gas at constant pressure decreases, roughly according to the ideal gas law,

PV=RT (1.1)

Correspondingly the entropy of the gas decreases.

However this ideal gas behaviour does not continue indefinitely as the temperature T is lowered. Instead, the interactions between molecules take over as their kinetic energy (of order k_BT ) where k_B is Boltzmann’s constant) becomes smaller and their spacing is reduced. At the boiling point (around 77 K for nitrogen) a sudden phase change occurs and the substance condenses into a liquid. The liquid is a phase of higher orderliness (lower entropy) because the density is so much higher than in the gas phase. The latent heat L of the phase transition speaks directly of this entropy reduction ΔSsince L=TΔS.

In the liquid phase, the nitrogen molecules remain highly mobile with kinetic energy still of order k_BT. As T is reduced further, there comes a point where the liquid freezes (about 63K for nitrogen) to become a solid. Another, latent heat demonstrates the advent of this even more ordered phase, in which molecules are effectively localised on to well-defined lattice sites.

Further reduction in temperature produces no further changes of phase. The quantum ground state of the solid corresponds to all molecules being located at their lattice sites as securely as possible and having the minimum possible vibrational energy. It is as well to recall that this minimum energy is not zero, however, because of Heisenberg’s uncertainty principle. For example, a simple (one-dimensional) harmonic oscillator has a minimum (“zero-point”) energy of 1/2 hν where h is Planck’s constant and ν the classical oscillator frequency, since the oscillating particle cannot simultaneously have its position certain and its momentum definitely zero. This type of consideration affects each degree of freedom in the solid.

Above absolute zero, the solid has vibrational energy usually described as a gas of phonons. As the absolute zero is approached, these thermal phonons are simply frozen out, a situation analogous to the freezing out of thermal photons, i.e. black-body radiation, in an “empty” box containing only electromagnetic radiation. This is possible because phonons (and photons) are particles whose number is not conserved, so that they can simply disappear as T is reduced without any problem. In this respect, the statistical physics of such a “phony” gas (pun intended!) differs dramatically from that of a real gas, as we shall see below.

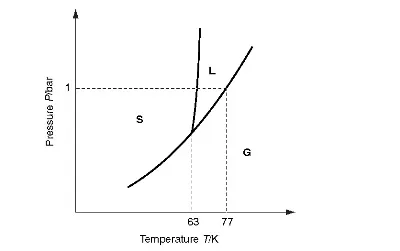
Figure 1.1 The phase diagram of nitrogen (schematic). Note the triple point at 63 K and the normal boiling point at 77 K.

The phase diagram of nitrogen in Figure 1.1 illustrates its ordering behaviour and the existence of the three common phases: gas, liquid and solid. Note that the existence of a triple point ensures that at absolute zero the only possible phase is the solid. One can note that it is only because the triple point pressure is below one atmosphere (1 bar) that we experience the liquid phase at all, under common conditions. Contrast carbon dioxide, triple point pressure 5 bar, which we meet as a gas or as a cold solid, “dry ice”, or recall that nitrogen forms the dry ice of Triton (Neptune’s largest moon) which has an atmospheric pressure of a minute 1.5 × 10^-5 bar and a temperature of 38 K.

1.1.2 Ordering in not so simple substances

In practice, ordering at low temperatures can of course be more complex than that of the above. There are two major types of complications which have been brushed under the carpet in the discussion so far, even before we get on to the topic of superfluids.

The first complication to be recognised is that there are several important contributions to the thermal properties of many substances, other than the simple molecular motion discussed above. Hence there are other entropy contributions to be considered in practice. For example, in many materials we do not have essentially isolated molecules, but in the solid and/or liquid states the proximity of atoms leads to electronic overlap and hence to non-localised electronic motion, often giving rise to metallic or semiconducting properties. Indeed it is the existence of such an electron gas at the lowest temperature which leaves the way open for superconductivity, as we shall see. Then, secondly, there is the existence of degrees of freedom associated with electronic and nuclear spin and with orbital motion of electrons around nuclei, all of which lead to magnetic properties. The consequent ordering of electronic or nuclear spins at low temperatures gives a variety of important phenomena. Thirdly, there are structural phase transitions in many solids, arising from the subtle way in which interatomic interactions vary with separation and direction. Fourthly, we can have contributions from defects and vacancies.

As if that is not enough to consider in real life, there is another type of complication entirely. This relates to whether the substance under discussion is in fact in thermal equilibrium. This is a matter of time scales. At low temperatures, the time scale for thermal equilibrium to be achieved can become effectively infinite for some types of reordering, particularly those involving the movement of molecules. Hence disorder is frozen in as the temperature is lowered. A classic example is that of a glass, where even at room temperature the molecules form a disordered and unpredictable array rather than a regular crystalline structure. And the glassy structure once formed remains in the same state for a very long time. Thus the true quantum mechanical ground state of the system is never accessible.

In contrast, in the situations where superfluids are found, the ground state is certainly accessible. Indeed it is the coherent quantum nature of this state which plays a central role in the observable properties of the substance. But before discussing this further, we take a closer look at the Third Law and its implications.

1.2 THE THIRD LAW OF THERMODYNAMICS AND ORDERING

The Third Law of Thermodynamics, originally called the Nernst Heat Theorem after it was formulated by Nernst in 1906, was a matter of considerable controversy until it was clarified by Sir Francis Simon in the 1930s.¹ Stated in its strongest form the law simply says that “the entropy of any substance must go to zero as the absolute zero of temperature isreached”. The difficulty of this formulation is obvious from the discussion of the previous section. It is not going to be either true or very useful if the substance never reaches its true thermodynamic equilibrium state.

The entropy Sof a substance can be expressed in terms of its possible quantum states (so-called microstates) as

S=K_B ln Ω (1.2)

where Ω is the number of possible quantum states which the whole system can achieve. This expression, first formulated by Boltzmann and extended by Planck, gives a valuable statistical interpretation of the meaning of entropy. Zero entropy thus implies that the system must have Ω=1, i.e. that it must certainly have entered its ground state. Hence another way of looking at the Third Law is that it states that “any substance must reach its ground state as it approaches T= 0” .

1.2.1 Is equilibrium reached?

A modern view of the Third Law includes a consideration of equilibrium times. The key, as recognised by Simon, is to recognise explicitly that there are many independent contributions to the entropy of a typical substance. In other words, there are many quantum numbers which must be specified to describe the quantum state of the system. Take, for example, a block of copper metal. This has (at least) the following possible contributions to its entropy:

1. Lattice vibrations, phonons.
2. Conduction electrons.
3. Nuclear spins, since both isotopic constituents ⁶³Cu and ⁶⁵Cu have spin 3/2.
4. Isotopic disorder from arrangements in the crystal lattice of ⁶³Cu and ⁶⁵Cu.
5. Crystalline imperfections (grain boundaries, dislocations, vacancies).

Now the point is that, as a broad approximation, one can divide such contributions to the disorder of a substance into two classes. First, there are those which come to equilibrium under the relevant experimental con...

Table of contents

• COVER PAGE
• TITLE PAGE
• COPYRIGHT PAGE
• FIGURES
• PREFACE
• CHAPTER 1 WHAT HAPPENS AT LOW TEMPERATURES?
• CHAPTER 2 LIQUID 4HE
• CHAPTER 3 EXPERIMENTAL TECHNIQUES
• CHAPTER 4 SUPERCONDUCTIVITY
• CHAPTER 5 LIQUID 3HE
• ANSWERS TO THE PROBLEMS