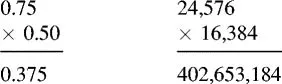Digital Signal Processing 101

Everything You Need to Know to Get Started

Michael Parker

• Publisher: Newnes
• Year: 2010
• eBook ISBN: 9781856179225
• Topic: Technology & Engineering
• Subtopic: Signals & Signal Processing
• Index: Technology & Engineering

Digital Signal Processing 101: Everything You Need to Know to Get Started provides a basic tutorial on digital signal processing (DSP). Beginning with discussions of numerical representation and complex numbers and exponentials, it goes on to explain difficult concepts such as sampling, aliasing, imaginary numbers, and frequency response. It does so using easy-to-understand examples and a minimum of mathematics. In addition, there is an overview of the DSP functions and implementation used in several DSP-intensive fields or applications, from error correction to CDMA mobile communication to airborne radar systems. This book is intended for those who have absolutely no previous experience with DSP, but are comfortable with high-school-level math skills. It is also for those who work in or provide components for industries that are made possible by DSP. Sample industries include wireless mobile phone and infrastructure equipment, broadcast and cable video, DSL modems, satellite communications, medical imaging, audio, radar, sonar, surveillance, and electrical motor control.- Dismayed when presented with a mass of equations as an explanation of DSP? This is the book for you!- Clear examples and a non-mathematical approach gets you up to speed with DSP- Includes an overview of the DSP functions and implementation used in typical DSP-intensive applications, including error correction, CDMA mobile communication, and radar systems

CHAPTER 1
Numerical Representation

To process a signal digitally, it must be represented in a digital format. This point may seem obvious, but it turns out that there are a number of different ways to represent numbers, and this representation can greatly affect both the result and the number of circuit resources required to perform a given operation. This chapter is focused more for people who are implementing digital signal processing (DSP) and is not really required to understand DSP fundamental concepts.

Digital electronics operate on bits, of course, which are used to form binary words. The bits can be represented as binary, decimal, octal, hexadecimal, or another form. These binary numbers can be used to represent “real” numbers. There are two basic types of arithmetic used in DSP: floating point and fixed point. Fixed-point numbers have a fixed decimal point as part of the number. Examples are 1234 (the same as 1234.0), 12.34, and 0.1234. This is the type of number we normally use every day. A floating-point number has an exponent. The most common example is scientific notation, used on many calculators. In floating point, 1,200,000 would be expressed as 1.2 × 10⁶, and 0.0000234 would be expressed as 2.34 × 10^–5. Most of our discussion will focus on fixed-point numbers, as they are most commonly found in DSP applications. Once we understand DSP arithmetic issues with fixed-point numbers, then there is short discussion of floating-point numbers.

In DSP, we pretty much exclusively use signed numbers, meaning that there are both positive and negative numbers. This leads to the next point, which is how to represent the negative numbers.

In signed fixed-point arithmetic, the binary number representations include a sign, a radix or decimal point, and the magnitude. The sign indicates whether the number is positive or negative, and the radix (also called decimal) point separates the integer and fractional parts of the number.

The sign is normally determined by the leftmost, or most significant bit (MSB). The convention is that a zero is used for positive and one for negative. There are several formats to represent negative numbers, but the almost universal method is known as 2s complement. This is the method discussed here.

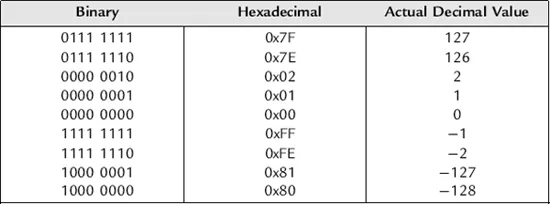
Furthermore, fixed-point numbers are usually represented as either integer or fractional. In integer representation, the decimal point is to the right of the least significant bit (LSB), and there is no fractional part in the number. For an 8-bit number, the range that can be represented is from −128 to +127, with increments of 1.

In fractional representation, the decimal point is often just to the right of the MSB, which is also the sign bit. For an 8-bit number, the range that can be represented is from −1 to +127/128 (almost +1), with increments of 1/128. This may seem a bit strange, but in practice, fractional representation has advantages, as will be explained.

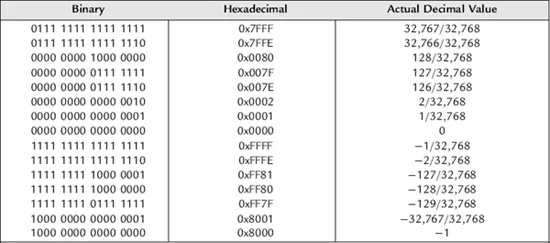
This chapter presents several tables, with each row giving equivalent binary and hexadecimal numbers. The far right column gives the actual value in the chosen representation—for example, 16-bit integer representation. The actual value represented by the hex/binary numbers depends on which representation format is chosen.

1.1 Integer Fixed-Point Representation

The following table provides some examples showing the 2s complement integer fixed-point representation.

Table 1.1: 8-Bit integer representation

The 2s complement representation of the negative numbers may seem nonintuitive, but it has several very nice features. There is only one representation of 0 (all 0s), unlike other formats that have a “positive” and “negative” zero. Also, addition and multiplication of positive and negative 2s complement numbers work properly with traditional digital adder and multiplier structures. A 2s complement number range can be extended to the left by simply replicating the MSB (sign bit) as needed, without changing the value.

The way to interpret a 2s complement number is to use the mapping for each bit shown in the following table. A 0 bit in a given location of the binary word means no weight for that bit. A 1 in a given location means to use the weight indicated. Notice the weights double with each bit moving left, and the MSB is the only bit with a negative weight. You should satisfy yourself that all negative numbers will have an MSB of 1, and all positive numbers and zero have an MSB of 0.

Table 1.2: 2s complement bit weighting with 8 bit words

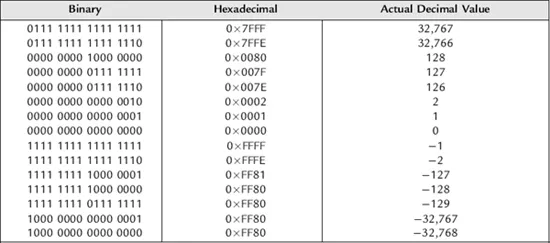
This can be extended to numbers with larger number of bits. Following is an example with 16 bits. Notice how the numbers represented in a lesser number of bits (e.g., 8 bits) can be easily put into 16-bit representation by simply replicating the MSB of the 8-bit number eight times and tacking onto the left to form a 16-bit number. Similarly, as long as the number represented in the 16-bit representation is small enough to be represented in 8 bits, the leftmost bits can simply be shaved off to move to the 8-bit representation. In both cases, the decimal point stays to the right of the LSB and does not change location. This can be seen easily by comparing, for example, the representation of −2 in the 8-bit representation table and again in the 16-bit representation table.

Table 1.3: 16-Bit signed integer representation

Table 1.4: 2s complement bit weighting with 16 bit word

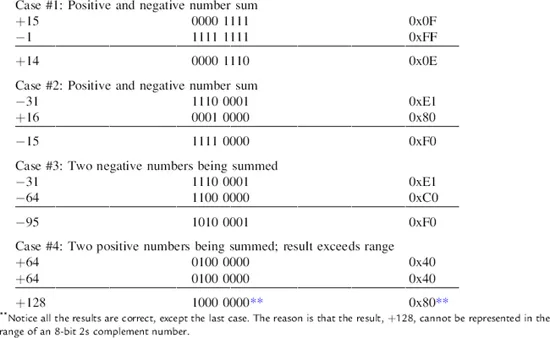
Now, let’s look at some examples of trying to adding combinations of positive and negative 8-bit numbers together using a traditional unsigned digital adder. We throw away the carry bit from the last (MSB) adder stage.

Integer representation is often used in many software applications because it is familiar and works well. However, in DSP, integer representation has a major drawback. In DSP, there is a lot of multiplication. When you multiply a bunch of integers together, the results start to grow rapidly. It quickly gets out of hand and exceeds the range of values that can be represented. As we saw previously, 2s complement arithmetic works well, as long as you do not exceed the numerical range. This has led to the use of fractional fixed-point representation.

1.2 Fractional Fixed-Point Representation

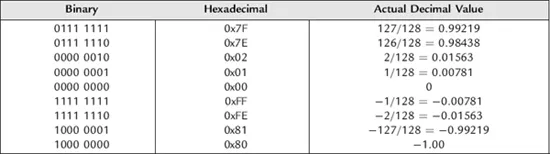
The basic idea behind fractional fixed-point representation is all values are in the range from +1 to – 1, so if they are multiplied, the result will not exceed this range. Notice that, if you want to convert from integer to 8-bit signed fractional, the actual values are all divided by 128. This maps the integer range of +127 to −128 to almost +1 to −1.

Table 1.5: 8-Bit fractional representation

Table 1.6: 2s complement weighting for 8 bit fractional word

Table 1.7: 16-Bit signed fractional representation

Table 1.8: 2s complement weighting for 16 bit fractional word

Fractional fixed point is often expressed in Q format. The representation shown above is Q15, which means that there are 15 bits to the right of the radix or decimal point. It might also be called Q1.15, meaning that there are 15 bits to right of the decimal point and one bit to the left.

The key property of fractional representation is that the numbers grow smaller, rather than larger, during multiplication. And in DSP, we commonly sum the results of many multiplication operations. In integer math, the results of multiplication can grow large quickly (see the following example). And when we sum many such results, the final sum can be very large, easily exceeding the ability to represent the number in a fixed-point integer format.

As an analogy, think about trying to display an analog signal on an oscilloscope. You need to select a voltage range (volts/division) in which the signal amplitude does not exceed the upper and lower range of the display. At the same time, you want the signal to occupy a reasonable part of the screen, so the detail of the signal is visible. If the signal amplitude occupies only 1/10 of a division, for example, it is difficult to see the signal.

To illustrate this situation, imagine using a 16-bit fixed point, and the signal has a value of 0.75 decimal or 24,676 in integer (which is 75% of full scale), and is multiplied by a coefficient of value 0.50 decimal or 16,384 integer (which is 50% of full scale).

Now the larger integer number can be shifted right after every such operation to scale the signal within a range that it can be represented, but most DSP designers prefer to represent numbers as fractional because it is a lot easier to keep track of the decimal point.

Now consider multiplication again. If two 16-bit numbers are multiplied, the result is a 32-bit number. As it turns out, if the two numbers being multiplied are Q15, you might expect the result in the 32-bit register to be a Q31 number (MSB to the left of the decima...

Table of contents

• Cover
• Title
• Copyright
• Introduction
• Acknowledgments
• Chapter 1 Numerical Representation
• Chapter 2 Complex Numbers And Exponentials
• Chapter 3 Sampling, Aliasing, And Quantization
• Chapter 4 Frequency Response
• Chapter 5 Finite Impulse Response (FIR) Filters
• Chapter 6 Windowing
• Chapter 7 Decimation And Interpolation
• Chapter 8 Infinite Impulse Response (Iir) Filters
• Chapter 9 Complex Modulation And Demodulation
• Chapter 10 Discrete And Fast Fourier Transforms (Dft, Fft)
• Chapter 11 Digital Upconversion And Downconversion
• Chapter 12 Error Correction Coding
• Chapter 13 Analog And Tdma Wireless Communications
• Chapter 14 Cdma Wireless Communications
• Chapter 15 Ofdma Wireless Communications
• Chapter 16 Radar Basics
• Chapter 17 Pulse Doppler Radar
• Chapter 18 Synthetic Array Radar
• Chapter 19 Introduction To Video Processing
• Chapter 20 Implementation Using Digital Signal Processors
• Chapter 21 Implementation Using Fpgas
• Appendix A Q Format Shift With Fractional: Multiplication
• Appendix B Evaluation Of Fir Design Error: Minimization
• Appendix C Laplace Transform
• Appendix D Z-Transform
• Appendix E Binary Field Arithmetic
• Index