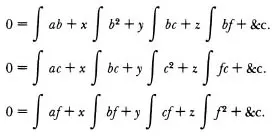The History of Statistics

The Measurement of Uncertainty before 1900

Stephen M. Stigler

• Publisher: Belknap Press
• Year: 1990
• ISBN:
  9780674256859
• Topic: History
• Subtopic: Modern History
• Index: History

This magnificent book is the first comprehensive history of statistics from its beginnings around 1700 to its emergence as a distinct and mature discipline around 1900. Stephen M. Stigler shows how statistics arose from the interplay of mathematical concepts and the needs of several applied sciences including astronomy, geodesy, experimental psychology, genetics, and sociology. He addresses many intriguing questions: How did scientists learn to combine measurements made under different conditions? And how were they led to use probability theory to measure the accuracy of the result? Why were statistical methods used successfully in astronomy long before they began to play a significant role in the social sciences? How could the introduction of least squares predate the discovery of regression by more than eighty years? On what grounds can the major works of men such as Bernoulli, De Moivre, Bayes, Quetelet, and Lexis be considered partial failures, while those of Laplace, Galton, Edgeworth, Pearson, and Yule are counted as successes? How did Galton's probability machine (the quincunx) provide him with the key to the major advance of the last half of the nineteenth century?Stigler's emphasis is upon how, when, and where the methods of probability theory were developed for measuring uncertainty in experimental and observational science, for reducing uncertainty, and as a conceptual framework for quantitative studies in the social sciences. He describes with care the scientific context in which the different methods evolved and identifies the problems (conceptual or mathematical) that retarded the growth of mathematical statistics and the conceptual developments that permitted major breakthroughs.Statisticians, historians of science, and social and behavioral scientists will gain from this book a deeper understanding of the use of statistical methods and a better grasp of the promise and limitations of such techniques. The product of ten years of research, The History of Statistics will appeal to all who are interested in the humanistic study of science.

PART ONE

The Development of Mathematical Statistics in Astronomy and Geodesy before 1827

1. Least Squares and the Combination of Observations

Adrien Marie Legendre (1752–1833)

THE METHOD of least squares was the dominant theme—the leitmotif—of nineteenth-century mathematical statistics. In several respects it was to statistics what the calculus had been to mathematics a century earlier. “Proofs” of the method gave direction to the development of statistical theory, handbooks explaining its use guided the application of the higher methods, and disputes on the priority of its discovery signaled the intellectual community’s recognition of the method’s value. Like the calculus of mathematics, this “calculus of observations” did not spring into existence without antecedents, and the exploration of its subtleties and potential took over a century. Throughout much of this time statistical methods were commonly referred to as “the combination of observations.” This phrase captures a key ingredient of the method of least squares and describes a concept whose evolution paced the method’s development. The method itself first appeared in print in 1805.

Legendre in 1805

In March of 1805 political Europe focused its attention uneasily on France. The 1801 Peace of Amiens was crumbling, and preparations were under way for a new round of war, one that would begin that autumn with the battle of Trafalgar and the opening of the Napoleonic campaigns with victories at Ulm and Austerlitz. Scientific Europe also looked to France; there the discipline was intellectual, not martial, and was subsequently more sure and longer lived than that of the new emperor of the French.

In March of 1805 Laplace celebrated his fifty-sixth birthday, prepared the fourth volume of his Traite de mécanique céleste for press, and, perhaps, began to return his thoughts to the completion of a book on probability he had first contemplated more than twenty years before. Also in March of 1805 another French mathematical scientist, Adrien Marie Legendre, sent to press the final pages of a lengthy memoir that contained the first publication of what is even today the most widely used nontrivial technique of mathematical statistics, the method of least squares.

Legendre (born 18 September 1752, died 10 January 1833) was a mathematician of great breadth and originality. He was three years Laplace’s junior and succeeded Laplace successively as professor of mathematics at the Ecole Militaire and the Ecole Normale. Legendre’s best-known mathematical work was on elliptic integrals (he pioneered this area forty years before Abel and Jacobi), number theory (he discovered the law of quadratic reciprocity), and geometry (his Eléments de géométrie was among the most successful of such texts of the nineteenth century). In addition, he wrote important memoirs on the theory of gravitational attraction. He was a member of two French commissions, one that in 1787 geodeticallyjoined the observatories at Paris and Greenwich and one that in 1795 measured the meridian arc from Barcelona to Dunkirk, the arc upon which the length of the meter was based. It is at the nexus of these latter works in theoretical and practical astronomy and geodesy that the method of least squares appeared.

In 1805 (the appendix we shall discuss is dated 6 March 1805) Legendre published the work by which he is chiefly known in the history of statistics, Nouvelles méthodes pour la détermination des orbites des comètes. At eighty pages this work made a slim book, but it gained a fifty-five-page supplement (and a reprinted title page) in January of 1806, and a second eighty-page supplement in August of 1820. The appendix presenting the method of least squares occupies nine of the first eighty pages; it is entitled “Sur la méthode des moindres quarrés.” For stark clarity of exposition the presentation is unsurpassed; it must be counted as one of the clearest and most elegant introductions of a new statistical method in the history of statistics. In fact, statisticians in the succeeding century and three-quarters have found so little to improve upon that, but for his use of ∫ instead of Σ to signify summation, the explanation of the method could almost be from an elementary text of the present day. Legendre began with a clear statement of his objective:

On the Method of Least Squares

In most investigations where the object is to deduce the most accurate possible results from observational measurements, we are led to a system of equations of the form

E = a + bx + cy + fz + &c.,

in which, a, b, c, f, &c. are known coefficients, varying from one equation to the other, and x, y, z, &c. are unknown quantities, to be determined by the condition that each value of E is reduced either to zero, or to a very small quantity. (Legendre, 1805, p. 72)

We might write this today as

E_i = a_i + b_ix + c_iy + f_iz + . . .

or

a_i= − b_ix − c_iy − f_iz − . . . + E_i,

but we would probably join Legendre in calling the E’s “errors.” When the number of equations equaled the number of unknowns, Legendre saw no problem. But when there were more equations than unknowns, it became impossible to choose values for the unknowns that would eliminate all the errors. He noted that there was an element of arbitrariness in any way of, as he put it, “distributing the errors among the equations,” but that did not stop him from dramatically proposing a single best solution:

Of all the principles that can be proposed for this purpose, I think there is none more general, more exact, or easier to apply, than that which we have used in this work; it consists of making the sum of the squares of the errors a minimum. By this method, a kind of equilibrium is established among the errors which, since it prevents the extremes from dominating, is appropriate for revealing the state of the system which most nearly approaches the truth. (Legendre, 1805, pp. 72–73)

Minimize the sum of the squares of the errors! How simple—but was it practical? Legendre wasted no time in writing down the equations he derived by differentiating the sum of squared errors (a + bx + cy + fz + &c.)² + (a′ + b′x + c′y + f′z + &c.)² + (a″ + b″x + c″y + f″z + &c.)² + &c. with respect to x, y, . . . , namely,

where by ∫ ab we understand the sum of the similar products ab + a′b′ + a″b″ + &c; and by ∫b² the sum of the squares of the coefficients of x, that is, b² + b′² + b″² + &c., and so on. (Legendre, 1805, p. 73)

Lest there be any doubt as to how to form these, the “normal equations” (a name introduced later by Gauss), Legendre restated the rule in italicized words:

In general, to form the equation of the minimum with respect to one of the unknowns, it is necessary to multiply all the terms of each equation by the coefficient of the unknown in that equation, taken with its proper sign, and then to find the sum of all these products. (Legendre, 1805, p. 73)

The equations, as many as there were unknowns, could then be solved by “ordinary methods.”

The practicality of Legendre’s principle was thus self-evident; all it required was a few simple multiplications and additions and the willingness to solve a set of linear equations. Because the latter step would be required in any case, even if the number of observations equaled the number of unknowns, the formation of the “equations of the minimum” was all that Legendre added to the calculations. It was a small computational price to pay for such an appealingly evenhanded resolution to a difficult problem. In case more convincing was needed, Legendre added these points:

(1) If a perfect fit were possible, his method would find it.

(2) If it were subsequently decided to discard an equation (say, if its “error” were too large), it would be a simple matter to revise the equations by subtracting the appropriate terms.

(3) The arithmetic mean was a special case of the method, found when there is a single unknown with constant coefficient b = b′ = . . . = 1.

(4) Likewise, finding the center of gravity of several equal masses in space was a special case. By analogy with this last case Legendre closed his introduction of the method with these words, “We see, therefore, that the method of least squares reveals, in a manner of speaking, the center around which the results of observations arrange themselves, so that the deviations from that center are as small as possible” (Legendre, 1805, p. 75).

Legendre followed this explanation with a worked example using data from the 1795 survey of the French merid...