Multiphase Flow Analysis Using Population Balance Modeling

Bubbles, Drops and Particles

Guan Heng Yeoh, Dr. Chi Pok Cheung, Jiyuan Tu

• Publisher: Butterworth-Heinemann
• Year: 2013
• Print ISBN: 9780080982298
• eBook ISBN: 9780080982335
• Topic: Physical Sciences
• Subtopic: Fluid Mechanics

Written by leading multiphase flow and CFD experts, this book enables engineers and researchers to understand the use of PBM and CFD frameworks. Population balance approaches can now be used in conjunction with CFD, effectively driving more efficient and effective multiphase flow processes. Engineers familiar with standard CFD software, including ANSYS-CFX and ANSYS–Fluent, will be able to use the tools and approaches presented in this book in the effective research, modeling and control of multiphase flow problems. - Builds a complete understanding of the theory behind the application of population balance models and an appreciation of the scale-up of computational fluid dynamics (CFD) and population balance modeling (PBM) to a variety of engineering and industry applications in chemical, pharmaceutical, energy and petrochemical sectors - The tools in this book provide the opportunity to incorporate more accurate models in the design of chemical and particulate based multiphase processes - Enables readers to translate theory to practical use with CFD software

Chapter 1

Introduction

Abstract

Different classifications of multiphase flows that are found in many diverse natural, biological and industrial systems are described. Analyzing multiphase flows generally requires the understanding of the micro-physics controlling the organization of different phases in specific multiphase flows across different length scales. Effective utilization of computational approaches based on direct numerical simulation to probe into the behaviors of different classifications of multiphase flows is demonstrated. Nevertheless, current limiting computational resources points towards the need of population balance modelling and when coupled with computational fluid dynamics, the behavior and dynamic evolution of the population of gas bubbles, liquid drops and solid particles can be aptly analyzed for practical multiphase flow systems because of its comparatively lower computational requirements.

Keywords

agglomeration; aerocolloidal system; coalescence; energy exchange; fluid force; interphase mass; phase flow; van der Waals forces

1.1 Classification and Application of Multiphase Flows

Multiphase flows can be viewed as a fluid flow system comprising two or more distinct phases simultaneously co-flowing in a mixture where the level of separation between phases is at a scale well above the molecular level. In principle, multiphase flows can be classified on the basis of number of phases, types of phases, size of phases and interaction between phases. Depending on the combination of different phases, multiphase flows can be further classified according to: dispersed phase flows, separated phase flows, gas–liquid flows, liquid–liquid flows, gas–particle flows, liquid–particle flows, and three-phase flows.

Dispersed phase flows can be considered as flows whereby one of the phases exists as discrete particles. Two classical examples are the motion of bubbles in a liquid flow and the motion of liquid droplets in a gas. In such flows, there is no connection between these discrete fluid particles in the liquid. It is thus taken as a mixture of different sized bubbles or droplets that are being dispersed in a continuous medium.

Separated phase flows are different from dispersed phase flows due to the prevalence of a distinct line of contact separating two phases. One example is annular flow where there is a liquid layer along the pipe wall and a gaseous inner core. Categorically, one phase in this type of flow is distinctly separated from another in the same medium.

Gas–liquid flows having one phase being in gaseous form and the other in liquid state can assume many forms. Since the gas phase is permitted to freely deform within the liquid phase, several different geometrical shapes are possible, which include spherical, elliptical, distorted, toroidal and cap. Such flows also often exhibit other complex interfacial structures, namely, mixed or transitional flows that depict the transition between the dispersed phase flows and separated phase flows. Change of interfacial structures occurs through the occurrence of bubble–bubble or droplet–droplet interactions due to coalescence and break up and the presence of any phase change process.

Liquid–liquid flows belong to the special category where two immiscible fluids are co-flowing within the medium. One typical example is the presence of oil droplets in water or vice versa.

Gas–particle flows are concerned with the motion of suspended solid particles in the gas phase. For small particle number density, the gas flow exerts the main effect on the particles. Dilute gas–particle flows are predominantly governed by the surface and body forces acting on the particles. For very dilute gas–particle flows, the solid particles are treated as passive tracers, which do not have an effect on the gas flow. For large particle number density, particle–particle interactions become more important than the forces due to interstitial gas. Such two-phase flows are referred to as dense gas–particle flows. Collisions inherently exist between the solid particles and significantly influence their movement and migration in the gas phase. For substantially bigger particles, such flows are categorically known as granular flows.

Liquid–particle flows, in contrast to gas–particles flows, consist of the transport of solid particles in liquid flow instead. Here, the solid particles do not have a distinct velocity field but generally follow the liquid velocity field. Also known as slurry flows, they fall into the same category as dispersed phase flows in which the liquid now represents the continuous medium. The different liquid and solid phases are mainly driven by, and largely respond to, the presence of pressure gradients since the density ratio between phases is low and the drag between phases is generally rather high in such flows.

Three-phase flows are encountered in a number of engineering applications of technical relevance, for example, bubbles in slurry flows resulting in three phases co-flowing together in the same medium. In this particular category, solid particles and gas bubbles co-flow with the continuous liquid phase. The coexistence of three phases considerably complicates the computational modeling of the flow physics due to the required understanding associated with the phenomena of particle–particle, bubble–bubble, particle–bubble, particle–fluid, and bubble–fluid interactions.

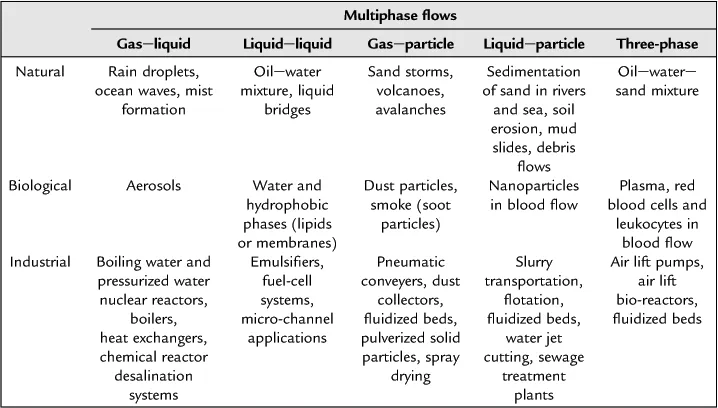
Based on the above classifications, multiphase flows are also widely featured in many diverse natural, biological, and industrial systems. Some examples of multiphase flows that can be distinguished in these three different systems are illustrated in Table 1.1. It should be noted that the list of examples presented in this table is by no means exhaustive but is intended to provide the reader a broad overview of the range of applications and types of multiphase flows that can be found in these systems.

Table 1.1

Examples of multiphase flows in natural, biological and industrial systems.

Multiphase flows are inherently complex. The physical understanding of flows where more than one phase is involved offers problems of complexity that are immeasurably far greater than in single-phase flows. This is because the phases do not, in general, uniformly mix and because small-scale interactions between the phases can have profound effects on the macroscopic properties of the fluid flow. This clearly reflects the ubiquitous challenges that still exist when dealing with the complex nature of multiphase flows.

1.2 Complexity of Multiphase Flows

Dispersed flows of gas bubbles, liquid drops and solid particles are central to the analysis of multiphase flows and development of generic computational approaches. The motion of these particles is strongly affected by the relative motion of the phases within the mixture. As the relative motion becomes large enough, inertial instabilities can give rise to mesoscale structures (Agrawal et al., 2001). The complex nature of such flows is manifested by the appearance of clusters of bubbles, drops or particles (Serizawa, 2003).

In dispersed flows of bubbles or drops, the existence of dynamically changing interface can cause individual gas bubbles or liquid drops to deform, coalesce through the breaking down of the interfaces between the phases to form larger bubbles or drops, and break up into two smaller bubbles or drops due to the shearing of the fluid. As the volume flow of gases or drops increases, coalescence causes the appearance of caplike gas bubbles or liquid drops. For small diameter tubes, a pattern is exhibited whereby slugs of highly aerated liquid fill the whole tube. These so-called Taylor bubbles or drops have characteristics of a spherical cap nose and are somewhat abruptly terminated at the bottom edge. With increasing volume fractions of gases or drops, a churn pattern persists resulting in a haphazard flow of gas–liquid or liquid–liquid mixture. In contrast to small diameter tubes, churn flow can be rather different in large diameter pipes where Taylor bubbles are not formed. At very high velocities of the dispersed phase, an annular pattern is observed whereby part of the liquid flows along the wall and the remainder is the dispersed phase. The complexity of flow regime transitions remains an important problem whereby an improved physical understanding of one flow regime to another is required to establish a sound physical theory for the prediction of the different flow patterns.

In dispersed flows of solid particles, the entire range of particle volume fractions from dilute to dense conditions results in an array of complex physical processes. For dilute particle laden flows with high mass loading ratio, the motion of fluid has a significant effect on the particle motion and vice versa, when present. Interparticle collisions, which may be significant especially in “fluid-like” suspensions, can lead to particles interacting through interstitial fluid and ephemeral impulsive interactions. For conditions leading to transition from fluid-like to “solid-like” behavior, such as in a random close packing environment, not only particles will interact with each other through enduring contact between each other but also aggregation between individual solid particles may occur if the net interparticle force is attractive and strong enough to overcome the hydrodynamic forces. Conversely, breakage of the aggregate may be affected by the fluid shear overcoming the attractive interparticle force, which holds the individual solid particles together within the aggregate.

Principally, the difficulty in analyzing multiphase flows lies in the unconstrained behavior of the phases, which can assume a large number of complicated configurations. The main issue toward the understanding of why the phases configure in a particular way requires the identification of the microphysics controlling the organization of the phases of specific multiphase flows. For gas–liquid or liquid–liquid flows, the microphysics problem is the physical understanding of the formation or destruction of the changing interfaces between the fluid and gas bubbles or liquid drops. For gas–particle or liquid–particle flows, since the interfaces remain intact, the microphysics problem predominantly concerns the interfacial forces and interaction behaviors between particles. In turbulent multiphase flows, the possible interactions between turbulent eddies and interfacial structures as well as exchanges between individual phases introduce additional complexities to the flow phenomena. Under some circumstances, the discrete gas bubbles, liquid drops or solid particles can assume large-scale turbulent motions that do not directly reflect the turbulence patterns being observed in the fluid.

One recurring theme throughout the study of multiphase flows is the requirement to model and predict the detailed behavior of such flows and the phenomena that they continue to manifest. Computation of multiphase flows serves many essential roles: (1) as a tool to develop an understanding of the basic physics such as clarifying the importance of physical effects such as surface tension and gravity by adding or removing them, (2) as an aid in closing the averaged transport equations based upon a macroscopic formulation such as the development of closure relationships and testing against numerical simulations, and (3) as a means to solve actual problems such as small-scale problems that can be tackled through direct numerical simulation and large-scale problems via reduced formulations such as averaged transport equations. Computational techniques are becoming powerful tools to resolve a range of multiphase flows. The effective use of a variety of computational approaches to aptly handle different classifications of multiphase flows is demonstrated in Section 1.3.

1.3 Multiscale Characteristics of Multiphase Flows

Multiphase flow physics are inherently multiscale in nature. Figure 1.1 describes the many different physical characteristics that can be observed at different length scales. At microscale, it is essential to understand the interaction of the gas bubbles, liquid drops and solid particles with the continuum fluid through tracking the motion of the individual discrete particles in space and time. With increasing length scale, interaction between the discrete particles may become significant resulting in local structural changes due to agglomeration/coalescence and breakage/break up processes of gas bubbles, liquid drops and solid particles that are prevalent at the mesoscale. At the device scale, the influence of the macroscale hydrodynamic behavior of the background fluid on the clusters of gas bubbles, liquid drops and solid particles results in the existence of large-scale flow structures encompassing the different individual phases within the multiphase flow.

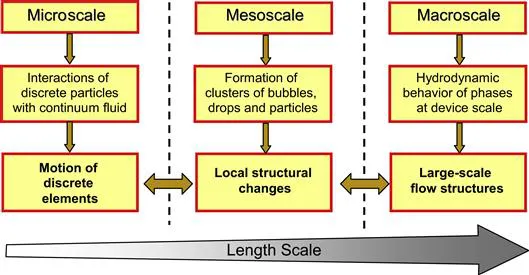
Figure 1.1 Multiscale characteristics of multiphase flows. (For color version of this figure, the reader is referred to the online version of this book.)

As will be illustrated through some examples below, computational techniques can be employed to reveal details of peculiar flow physics that otherwise could not be visualized by experiments or to clarify particular accentuating mechanisms that are consistently being manifested in complex multiphase flows. Such an approach, based on the utilization of advanced numerical methods and models, usually contains very detailed information, producing an accurate realization of the fluid flow.

Fujita and Yamaguchi (2007) have investigated the self-organization of nanoparticles in a dense suspension medium. Here, the motion of nanoparticles, which are treated as rigid spheres, is solved by the linear and angular momentum equations based on Newton’s law in a Lagrangian framework. The soft-sphere model based on the discrete element method is adopted to resolve the solid contact forces betwe...

Table of contents

• Cover image
• Title page
• Table of Contents
• Copyright
• Preface
• Foreword
• Acknowledgments
• Introduction
• Chapter 1. Introduction
• Chapter 2. Computational Multiphase Fluid Dynamics Framework
• Chapter 3. Population Balance Approach—A Generic Framework
• Chapter 4. Mechanistic Models for Gas–Liquid/Liquid–Liquid Flows
• Chapter 5. Mechanistic Models for Gas–Particle Liquid–Particle Flows
• Chapter 6. Solution Methods and Turbulence Modeling
• Chapter 7. Some Applications of Population Balance with Examples
• Chapter 8. Future of the Population Balance Approach
• References
• Index