Geophysical Data Analysis: Discrete Inverse Theory

MATLAB Edition

William Menke

• Publisher: Academic Press
• Year: 2012
• eBook ISBN: 9780123977847
• Edition: 3
• Topic: Physical Sciences
• Subtopic: Geophysics

Since 1984, Geophysical Data Analysis has filled the need for a short, concise reference on inverse theory for individuals who have an intermediate background in science and mathematics. The new edition maintains the accessible and succinct manner for which it is known, with the addition of: - MATLAB examples and problem sets - Advanced color graphics - Coverage of new topics, including Adjoint Methods; Inversion by Steepest Descent, Monte Carlo and Simulated Annealing methods; and Bootstrap algorithm for determining empirical confidence intervals - Additional material on probability, including Bayesian influence, probability density function, and metropolis algorithm - Detailed discussion of application of inverse theory to tectonic, gravitational and geomagnetic studies - Numerous examples and end-of-chapter homework problems help you explore and further understand the ideas presented - Use as classroom text facilitated by a complete set of exemplary lectures in Microsoft PowerPoint format and homework problem solutions for instructors

Chapter 1

Describing Inverse Problems

This chapter shows that inverse problems can be classified on the basis of the mathematical structure of the theory connecting the data and model parameters. The simplest theory is the explicit linear theory, which has the form of a matrix equation relating a vector of model parameters to a vector of data. The most complicated is the implicit nonlinear problem, in which the data and model parameters are mixed together in nonlinear relationships. A series of six exemplary inverse problems are discussed, starting with the simple notion of fitting a straight line to data exhibiting a linear trend, and culminating with acoustic tomography and X-ray imaging. In each case, the mathematical relationship between the data and model parameters is derived and classified. The meaning of the term solution to an inverse problem is debated; for depending upon the context and one’s point of view, any of several rather different quantities can be considered solutions. Solutions can include estimates of model parameters, deterministic or probabilistic bounds, probability density functions, and estimates of localized averages.

Keywords: Data, Model parameter, Theory, Forward problem, Inverse problem, Linear, Nonlinear, Implicit, Explicit, Data kernel, Estimates, Bounds, Localized average, Probability density function

1.1 Formulating Inverse Problems

The starting place in most inverse problems is a description of the data. Since in most inverse problems the data are simply a list of numerical values, a vector provides a convenient means of their representation. If N measurements are performed in a particular experiment, for instance, one might consider these numbers as the elements of a vector d of length N.

The purpose of data analysis is to gain knowledge through systematic examination of data. While knowledge can take many forms, we assume here that it is primarily numerical in nature. We analyze data so to infer, as best we can, the values of numerical quantities—model parameters. Model parameters are chosen to be meaningful; that is, they are chosen to capture the essential character of the processes that are being studied. The model parameters can be represented as the elements of a vector m, which is of length M

(1.1)

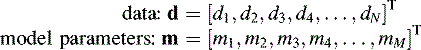
Here, T signifies transpose.

The basic statement of an inverse problem is that the model parameters and the data are in some way related. This relationship is called the quantitative model (or model, or theory, for short). Usually, the model takes the form of one or more formulas that the data and model parameters are expected to follow.

If, for instance, one were attempting to determine the density of an object, such as a rock, by measuring its mass and volume, there would be N = 2 data—mass and volume (say, d₁ and d₂, respectively)—and M = 1 unknown model parameter, density (say, m₁). The model would be the statement that density times volume equals mass, which can be written compactly by the vector equation d₂ m₁ = d₁. Note that the model parameter, density, is more meaningful than either mass or volume, in that it represents an intrinsic property of a substance that is related to its chemistry. The data—mass and volume—are easy to measure, but they are less fundamental because they depend on the size of the object, which is usually incidental.

In more realistic situations, the data and model parameters are related in more complicated ways. Most generally, the data and model parameters might be related by one or more implicit equations such as

(1.2)

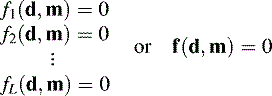
where L is the number of equations. In the above example concerning the measuring of density, L = 1 and d₂ m₁ − d₁ = 0 would constitute the one equation of the form f₁(d, m) = 0. These implicit equations, which can be compactly written as the vector equation f(d, m) = 0, summarize what is known about how the measured data and the unknown model parameters are related. The purpose of inverse theory is to solve, or “invert,” these equations for the model parameters, or whatever kinds of answers might be possible or desirable in any given situation.

No claims are made either that the equations f(d, m) = 0 contain enough information to specify the model parameters uniquely or that they are even consistent. One of the purposes of inverse theory is to answer these kinds of questions and provide means of dealing with the problems that they imply. In general, f(d, m) = 0 can consist of arbitrarily complicated (nonlinear) functions of the data and model parameters. In many problems, however, the equation takes on one of several simple forms. It is convenient to give names to some of these special cases, since they commonly arise in practical problems; we shall give them special consideration in later chapters.

1.1.1 Implicit Linear Form

The function f is linear in both data and model parameters and can therefore be written as the matrix equation

(1.3)

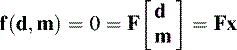
where F is an L × (M + N) matrix and the vector x = [d^T, m^T]^T is a concatenation of d and m, that is, x = [d₁, d₂, … , d_N, m₁, m₂, … , m_M]^T.

1.1.2 Explicit Form

In many instances, it is possible to separate the data from the mod...

Table of contents

• Cover image
• Title page
• Table of Contents
• Copyright
• Dedication
• Preface
• Introduction
• Chapter 1. Describing Inverse Problems
• Chapter 2. Some Comments on Probability Theory
• Chapter 3. Solution of the Linear, Gaussian Inverse Problem, Viewpoint 1: The Length Method
• Chapter 4. Solution of the Linear, Gaussian Inverse Problem, Viewpoint 2: Generalized Inverses
• Chapter 5. Solution of the Linear, Gaussian Inverse Problem, Viewpoint 3: Maximum Likelihood Methods
• Chapter 6. Nonuniqueness and Localized Averages
• Chapter 7. Applications of Vector Spaces
• Chapter 8. Linear Inverse Problems and Non-Gaussian Statistics
• Chapter 9. Nonlinear Inverse Problems
• Chapter 10. Factor Analysis
• Chapter 11. Continuous Inverse Theory and Tomography
• Chapter 12. Sample Inverse Problems
• Chapter 13. Applications of Inverse Theory to Solid Earth Geophysics
• Chapter 14. Appendices
• Index